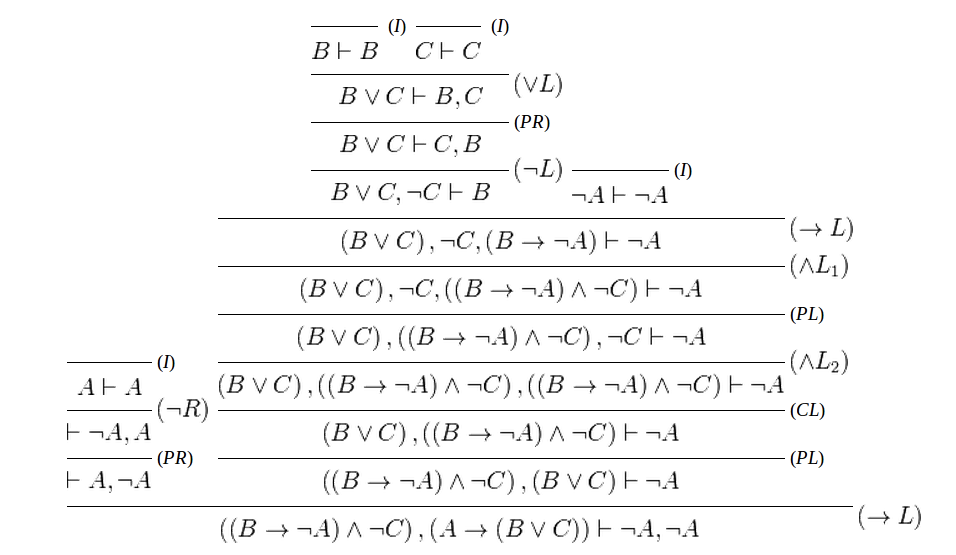小学生でも分かる論理計算 (A22P11)
※この記事は「記事22 問題集11」
伝達側が、省略なしに描いた絵を提示する労(と面積)を厭わず、学習者も絵を描く練習をするなら、専門家にも難解と言われるゲンツェン流の論理計算も、
内容的には小学生レベル
だと思います。
このこと(「絵を使えば簡単だぞ!」)をもっと過激に指摘しているのはボブ・クック〈Bob Coecke〉です。クックによれば、量子力学も絵で教えれば
幼稚園児レベル
だそうです。
- 幼稚園児のための量子力学とその周辺 2006年
- ボブ・クックの「物理系実務者のための圏論入門」 2007年
- 「物理系実務者のための圏論入門」への補遺+檜山の戯言 2007年
- ボブ・クックの「お絵描き大好き 量子絵図主義」 2010年
クック達(Oxford Quantum Group)は、絵で計算・証明を行うソフトウェア(QuantomaticとGlobular)を開発し公開してますが、それらの描画機能はイマイチで、絵は汎用お絵かきソフト(VisioとかBlender、TeXパッケージなど)で描いているようです。
量子テレポーテーションの絵:
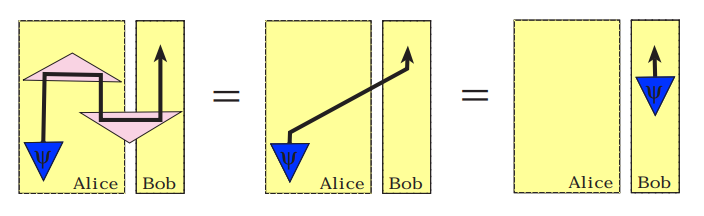 *1
*1
ロッカーでもあるクック先生の文言はけっこう“煽り”が入っているので、文字通りに「幼稚園児」は若干眉唾ですが、僕(檜山)が言っている「小学生」はたぶん可能だと思います。良いUIのソフトウェアがあれば、小学校低学年でも遊んでくれるでしょう。
内容:
- ゲンツェンのLKシーケント計算をご存知の方への注意
- 基本リーズニングの概要
- 基本推論
- 基本リーズニングの絵
- 練習問題
ゲンツェンのLKシーケント計算をご存知の方への注意
検索などでたまたまここに辿り着いた人が誤解するのも困るので、毎回この節を挿入することにします。
- '⇒'は含意〈条件法〉の論理結合子で、'→'がシーケントの左右を区切る記号である。
- ゲンツェンのLKシーケントでは、左辺のカンマは連言的に、右辺のカンマは選言的に解釈をする。ここでのシーケントでは、出現位置の情報を使わずに、カンマは常に連言的であり、選言的な区切り記号に縦棒'|'を使う。
- (x∈R, n∈N) のような書き方は、集合論の命題ではなくて、自由変数の型宣言(のリスト)である。自由変数の型宣言のリストをコンテキストと呼ぶ。
- 暗黙のコンテキストを使う場合もあるが、できるだけ、シーケント内に明示的にコンテキストを書き込むようにしている。
- NK/NJの証明図を推論図、LK/LJの証明図をリーズニング図と呼んで区別している。両方を同時に使うことがある。推論規則は、基本推論/基本リーズニングと呼ぶ。
- LK/LJのように、公理(基本推論)がひとつではなくて、けっこうたくさんの公理がある。その代わり、推論規則(基本リーズニング)の数を減らすようにしている。
基本リーズニングの概要
口頭で「5種類」と言ったような気がしますが、基本リーズニング〈primitive reasoning〉(システムに組み込みのリーズニング)は6種類です。「縦/横」は描画方向↓→で描く場合のことです。
| 番号 | 名前 | フルスペル | 一言説明 |
|---|---|---|---|
| 1 | Comp | composition | 結合、縦に繋げる |
| 2 | Prod | product | 論理積(連言)的な横併置 |
| 3 | Sum | sum | 論理和(選言)的な横併置 |
| 4 | Lamb | lambda | ラムダ抽象の論理版 |
| 5 | Diam | diamond | ∀限量子に関わるリーズニング |
| 6 | Squa | square | ∃限量子に関わるリーズニング |
Comp, Prod, Sum は2つの推論図から1つの推論図を作り出します。Lamb, Diam, Squa は1つの推論図から1つの推論図を作り出します。この他に、変数とコンテストを操作するリーズニングがあります(今回は触れない)。
リーズニングの働きに対応する演算子記号があります。lambda, diamond, squareは、演算子記号の形からの命名です。
| 番号 | リーズニング名 | 演算子記号 |
|---|---|---|
| 1 | Comp | ; |
| 2 | Prod | |
| 3 | Sum | |
| 4 | Lamb | Λ (大文字ラムダ) |
| 5 | Diam | ◇ |
| 6 | Squa | □ |
このなかで、最初の4つ、Comp, Prod, Sum Lamb は、次の理由で扱いが容易です。
- 変数・コンテストに関する操作がない(変数・コンテストを考えなくてもいい)。
- リーズニング下段の図(出力側)から、リーズニング上段の図(入力側)を再現可能。
Diam, Squa は、次の理由で難しいです。
- 変数・コンテストに関する操作が伴う。
- リーズニング下段の図から、リーズニング上段の図を再現するのが困難(たいていは不可能)。
今回は、比較的に簡単な Comp, Prod, Sum Lamb だけを説明します。Lambに関しては、既に詳しく説明しています、「Lambdaリーズニングと演繹原理〈演繹定理〉 (A20)」参照。
基本推論
基本リーズニングは、与えられた推論図の組み合わせ・変形を行う操作です。素材となる推論図が(描画方向↓→なら)上段になります。では、最初の推論図はどこから持ってくるのでしょう? “最初から在る”とみなす推論(図)を、基本推論〈primitive inference〉とか組み込み推論〈builtin inference〉と呼びます。
「シーケントとスコット・ブラケット (A10P8) // 組み込み推論を表すシーケント」に基本推論を列挙しています。
これらの基本推論には、名前が付いてます。歴史的な経緯から、ひとつの基本推論に幾つもの名前があります。例えば、プロファイルが A, A⇒B → B である基本推論は、「モーダスポネンス」、「三段論法(たぶん誤用)」、「eval(ラムダ計算から)」、「apply(ラムダ計算から)」、「ε(evalのeと、圏論の余単位から)」などと呼ばれます。
Xの恒等〈identity〉、Xの複製〈duplication〉、XとYの入れ替え〈swap〉などは、いちいち名前を書かないで、単なるワイヤー、ワイヤーの分岐、ワイヤーの交差で描きます。「スパイダーパズル (A17P10) // 汎用のスパイダー」参照。
基本リーズニングの絵
単一の命題は、A, B などのラテン文字で表します。命題のリスト(連言的リスト、または選言的リスト)は、Γ, Δ などのギリシャ文字で表します。リストの項目〈要素 | 成分〉が1個の場合は、単一の命題と同一視していいので、正確に言えば:
リストを、絵では二重線や太い線で表す人もいますが、ここでは単一の命題とリストを特に区別しないで、実線ワイヤーで描きます。
補助線、あるいは注釈線を赤で描くことにします。注釈線は、通常は省略します。ただし、
- Sumに対する注釈線(区切り線)がないと、ProdとSumの結果を区別できない。よって、Sumに対する注釈線、または注釈線に代わる何らかの目印が必要。
- Comp, Prodの注釈線(区切り線)は、なくてもよいが、ないと一意的にリーズニング図を再現することは出来なくなる。一意性を気にしないなら省略可能。
- Lambの注釈線(囲い)は、なくてもいい。
[追記]
完全に一意的な再現はやっぱり難しいなー。注釈の区切り線の長さを変えるとか、注釈として囲い枠を付けるとか、ゴチャゴチャと書き込めば一意的な再現が確かに可能ですが、そこまで注釈線を書き込むのが面倒過ぎる。
[/追記]
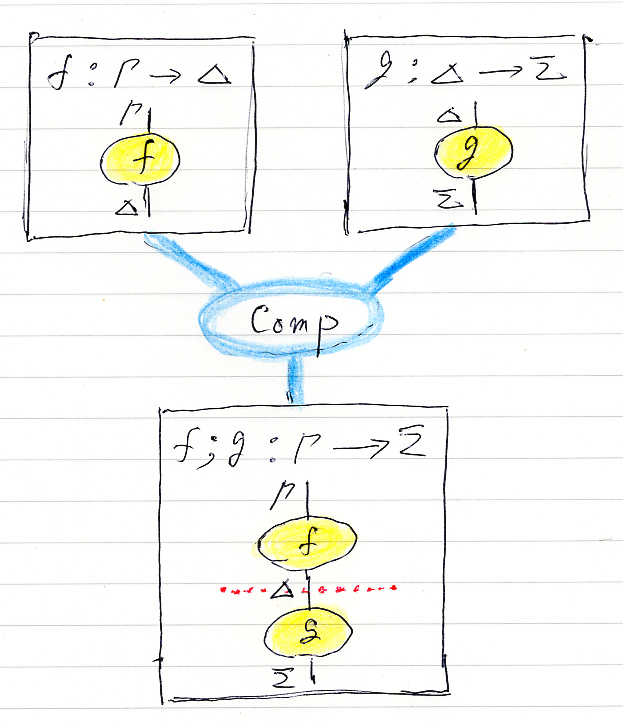
結合 Comp 基本リーズニング
上段の2つの推論図を縦に繋げます(あくまで、描画方向↓→での話)。左が上、右が下になります。繋いだ場所に、注釈の区切り線を横に入れます。
積 Prod 基本リーズニング
上段の2つの推論図を横に並べます。並べた中間に、注釈の区切り線を縦に入れます。
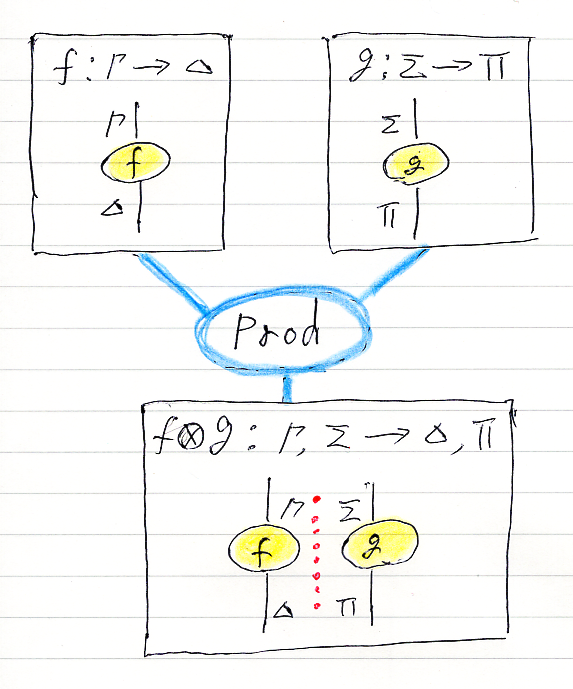
和 Sum 基本リーズニング
上段の2つの推論図を横に並べます。意味は、選言的な併置なので、積〈Prod〉とは違います。並べた中間に、注釈の区切り線を縦に実線で入れます。区切り線でなくても、積と区別するための何らかの目印が必須です。
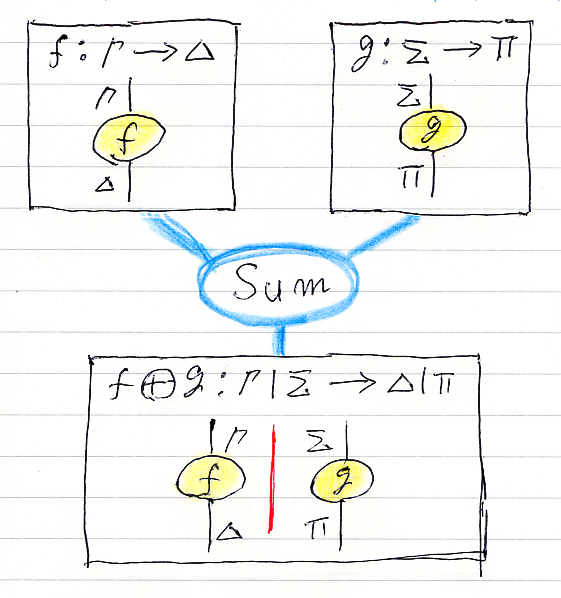
ラムダ Lamb 基本リーズニング
「Lambdaリーズニングと演繹原理〈演繹定理〉 (A20)」参照。囲いの注釈線はなくてもかまいません。とりあえず、曲げるワイヤーは一番左に限ることにします。こう制限しても、swapでワイヤーを入れ替えられるので心配は要りません。
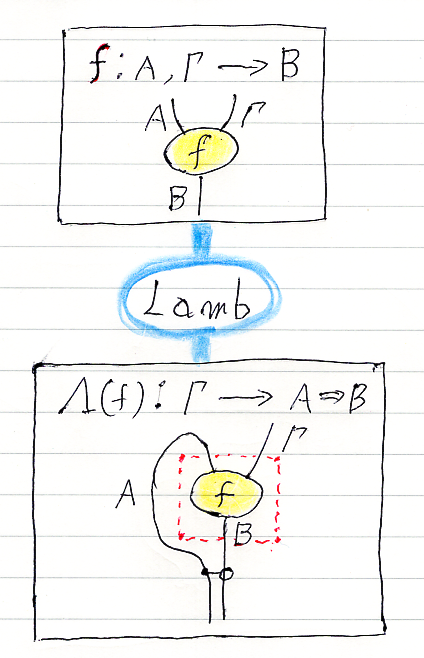
練習問題
Comp, Prod, Sum, Lamb だけしか使ってないなら、最後の推論図(出来上がり)から、構成過程であるリーズニング図が再現できます。注釈線までちゃんと描いてあれば、一意的に再現できます。
[追記]
先の追記で書いた事情で、完全に一意的な再現は難しいですね。結合律 (f;g);h = f;(g;h) の左右の違いのような差は生まれますが、それは同一視するなら、まーまー一意的です。
[/追記]
問題1: 下の推論図に対して、その構成過程であるリーズニング図を描いてください。全部乗せで、完全にグラフィカルなリーズニング図です。「全部乗せ」とは、フレーム(四角い枠)内に次を書き込むことです。
- 推論の名前、またはテキストによる式(演算子記号を使う)
- 推論図のプロファイル(シーケントとして書く)
- グラフィカルな推論図
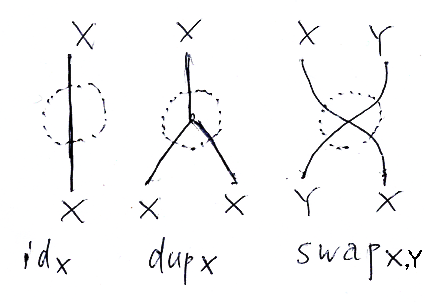
ワイヤーだけ、ワイヤーの分岐、ワイヤーの交差、ワイヤーの合流は次の記号で表します。
- idX
- dupX
- swapX, Y
- codupX (coは、sin, cos のcoと同じく、「相棒」を示す。)
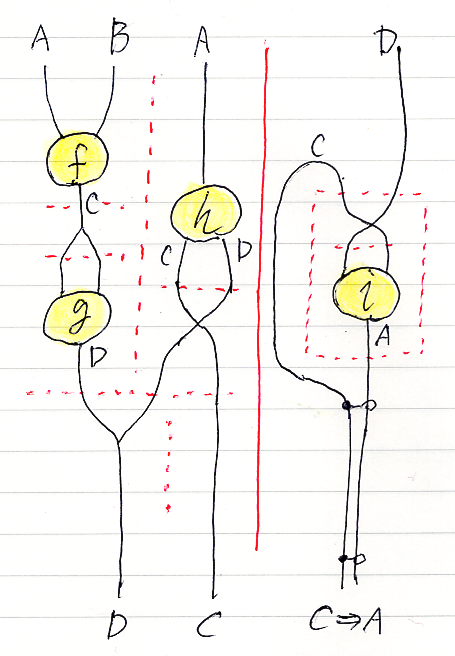
[追記]
「全部乗せで、完全にグラフィカルなリーズニング図」を描くのはムチャクチャ大変だわー。ゴメン、そこまでやんなくていいわ。真面目にやると、どの程度の労力と面積が必要かの見当がついたら、あとはテキトーに手を抜いていいです。
それと、上の図をそのままリーズニング図にすると、論理計算〈シーケント計算〉としてはちょっと具合が悪い点もありますね。解答のときに補足します。→ 解答例と修正と解説は、「問題集11「小学生でも…」の解答と補足説明 (A23R11)」
[/追記]
問題2: 完全なリーズニング図から、プロファイル(シーケント形式)だけを抜き出して、一本棒の横棒記法の図を作ってください。それが、論理の本でよくみる(例えば↓)シーケント証明図です。
「ゲンツェン流のシーケント計算が分からない」理由(の多く)は、何をどう扱っているかを知らないままに省略記法だけを機械的にいじるハメになるからです。