対称半リボン圏と擬内積ベクトル空間の圏
内積付きの線形代数の定式化として、対称半リボン圏がいいような気がした。いや、いいよ、これはいいよ、非常にいいよ。
まずリボン圏に関しては、
nLabの説明は矢鱈に短いが、リンクをたどれば納得できる。
リボン圏のベースとなるのはブレイド圏。それにツイストの族が付く。ツイストとバランシング/バランスは同じ意味。よって、形容詞twistedとbalancedも同じ。
半リボン圏のベースはブレイド付きコンパクト閉圏。全ひねり(full-twist)の代わりに半ひねり(half-twist)を入れたもの。半ひねりは、ρX:X→X*でリボン圏、プレ・リボン圏 - 檜山正幸のキマイラ飼育記 メモ編に書いた性質を持つ。
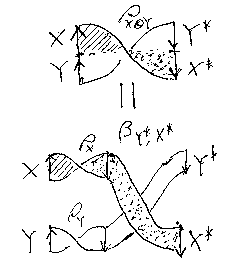
対称半リボン圏では、
- ブレイディングが対称である。つまり、対称モノイド圏になる。
- 半ひねりに関して、ρX;ρX*
X が成立する。このとき、X**
X を使う。(事前に、X**
X が必要。)
ベクトル空間の擬内積とは、内積から正定値性と対称性を除いたもの。擬内積を持つベクトル空間を対象として、線形写像(擬内積を保存する必要はない)を射とする圏を考える。Xの擬内積によって導かれる X→X*を、仮に擬内積の構造射(同型になる)と呼ぶ。
| 対称半リボン圏 | 擬内積空間の圏 |
|---|---|
| モノイド積 | テンソル積 |
| 単位対象 | スカラー体 |
| Xの双対対象 | Xの標準双対空間 |
| ev | 評価スカラー積 |
| coev | 単位行列に相当 |
| 半ひねり | 擬内積の構造射 |
| 射のスターメイト | 射の双対(共役、随伴) |
| 射のダガーメイト | 射の共役(双対、随伴) |
「双対、共役、随伴」は用語法が安定してないので、ケースバイケースで言葉と概念を割り当て直す必要がある。
この表の対応を使うと、擬内積空間の圏を非常にキレイに説明できる。
幾つかポイントを挙げれば:
- 二重双対がラウンドトリップする。ラウンドトリップ同型(involutive lawのrator)は自然同型で系統的に与える必要がある。
- 評価スカラー積(標準スカラー積、標準双線形形式)と擬内積は互いに定義しあうので、どちらがプライマリということはない。
- スター関手とダガー関手も、半ひねりを使って互いに定義しあえるので、どちらがプライマリということはない。
- スター関手の対合性=二重双対のラウンドトリップ性と半ひねりの対称性(これも対合性、ラウンドトリップ性)が肝。
- 半ひねりの存在により、自己双対なコンパクト閉圏が作れる。このときの双対メイトはダガーで与えられる。
- スター関手と半ひねりからダガー関手を作れるが、ダガー関手のみでスター関手と半ひねりを消してしまうことが出来る。これが内積オンリーな理論。
- 自己双対なコンパクト閉圏に、対合的なスター関手(ラウンドトリップ自然変換 involutive rator を持つ関手)を入れれば、自己双対ではないコンパクト閉圏を作れる。
- 擬内積が対称性(余可換性)を持てば、ベクトルのダガーメイト対応は、擬内積の構造射と一致する。
いやー、物凄くスッキリしたわ。