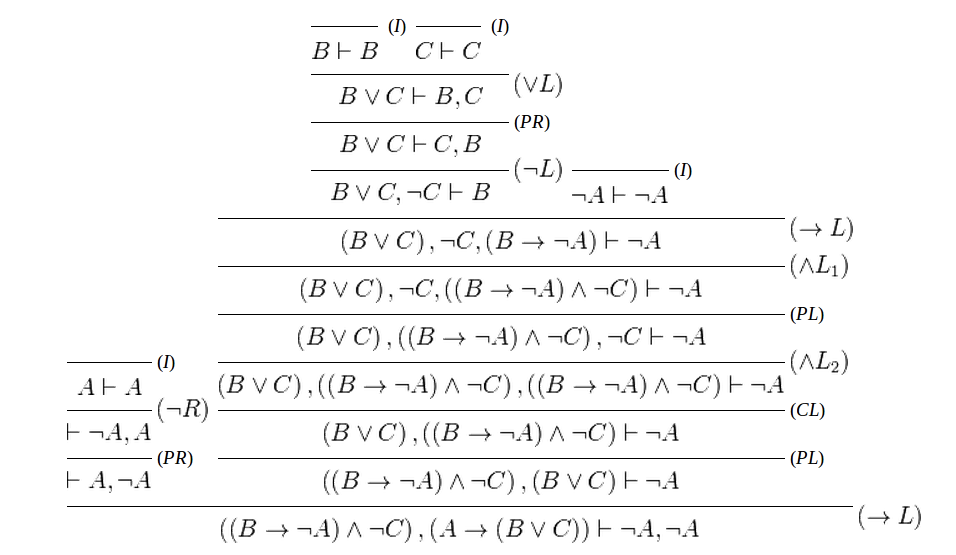小学生でも分かる論理計算 (A22P11)

※この記事は「記事22 問題集11」

伝達側が、省略なしに描いた絵を提示する労（と面積）を厭わず、学習者も絵を描く練習をするなら、専門家にも難解と言われるゲンツェン流の論理計算も、
内容的には小学生レベル
だと思います。

このこと（「絵を使えば簡単だぞ！」）をもっと過激に指摘しているのはボブ・クック〈Bob Coecke〉です。クックによれば、量子力学も絵で教えれば
幼稚園児レベル
だそうです。

• 幼稚園児のための量子力学とその周辺 2006年
• ボブ・クックの「物理系実務者のための圏論入門」 2007年
• 「物理系実務者のための圏論入門」への補遺＋檜山の戯言 2007年
• ボブ・クックの「お絵描き大好き 量子絵図主義」 2010年

クック達（Oxford Quantum Group）は、絵で計算・証明を行うソフトウェア（QuantomaticとGlobular）を開発し公開してますが、それらの描画機能はイマイチで、絵は汎用お絵かきソフト（VisioとかBlender、TeXパッケージなど）で描いているようです。

量子テレポーテーションの絵：
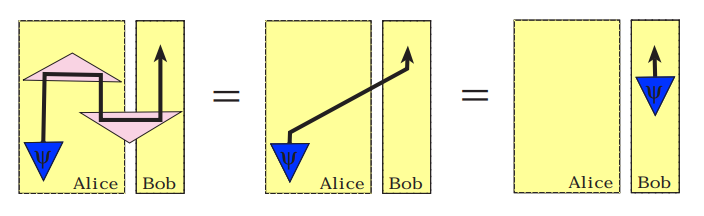*1

ロッカーでもあるクック先生の文言はけっこう“煽り”が入っているので、文字通りに「幼稚園児」は若干眉唾ですが、僕（檜山）が言っている「小学生」はたぶん可能だと思います。良いUIのソフトウェアがあれば、小学校低学年でも遊んでくれるでしょう。

*2

内容：

1. ゲンツェンのLKシーケント計算をご存知の方への注意
2. 基本リーズニングの概要
3. 基本推論
4. 基本リーズニングの絵
5. 練習問題

ゲンツェンのLKシーケント計算をご存知の方への注意

検索などでたまたまここに辿り着いた人が誤解するのも困るので、毎回この節を挿入することにします。

1. '⇒'は含意〈条件法〉の論理結合子で、'→'がシーケントの左右を区切る記号である。
2. ゲンツェンのLKシーケントでは、左辺のカンマは連言的に、右辺のカンマは選言的に解釈をする。ここでのシーケントでは、出現位置の情報を使わずに、カンマは常に連言的であり、選言的な区切り記号に縦棒'|'を使う。
3. (x∈R, n∈N) のような書き方は、集合論の命題ではなくて、自由変数の型宣言（のリスト）である。自由変数の型宣言のリストをコンテキストと呼ぶ。
4. 暗黙のコンテキストを使う場合もあるが、できるだけ、シーケント内に明示的にコンテキストを書き込むようにしている。
5. NK/NJの証明図を推論図、LK/LJの証明図をリーズニング図と呼んで区別している。両方を同時に使うことがある。推論規則は、基本推論／基本リーズニングと呼ぶ。
6. LK/LJのように、公理（基本推論）がひとつではなくて、けっこうたくさんの公理がある。その代わり、推論規則（基本リーズニング）の数を減らすようにしている。

基本リーズニングの概要

口頭で「5種類」と言ったような気がしますが、基本リーズニング〈primitive reasoning〉（システムに組み込みのリーズニング）は6種類です。「縦／横」は描画方向↓→で描く場合のことです。

番号	名前	フルスペル	一言説明
1	Comp	composition	結合、縦に繋げる
2	Prod	product	論理積（連言）的な横併置
3	Sum	sum	論理和（選言）的な横併置
4	Lamb	lambda	ラムダ抽象の論理版
5	Diam	diamond	∀限量子に関わるリーズニング
6	Squa	square	∃限量子に関わるリーズニング

Comp, Prod, Sum は2つの推論図から1つの推論図を作り出します。Lamb, Diam, Squa は1つの推論図から1つの推論図を作り出します。この他に、変数とコンテストを操作するリーズニングがあります（今回は触れない）。

リーズニングの働きに対応する演算子記号があります。lambda, diamond, squareは、演算子記号の形からの命名です。

番号	リーズニング名	演算子記号
1	Comp	;
2	Prod
3	Sum
4	Lamb	Λ （大文字ラムダ）
5	Diam	◇
6	Squa	□

このなかで、最初の4つ、Comp, Prod, Sum Lamb は、次の理由で扱いが容易です。

1. 変数・コンテストに関する操作がない（変数・コンテストを考えなくてもいい）。
2. リーズニング下段の図（出力側）から、リーズニング上段の図（入力側）を再現可能。

Diam, Squa は、次の理由で難しいです。

1. 変数・コンテストに関する操作が伴う。
2. リーズニング下段の図から、リーズニング上段の図を再現するのが困難（たいていは不可能）。

今回は、比較的に簡単な Comp, Prod, Sum Lamb だけを説明します。Lambに関しては、既に詳しく説明しています、「Lambdaリーズニングと演繹原理〈演繹定理〉 (A20)」参照。

基本推論

基本リーズニングは、与えられた推論図の組み合わせ・変形を行う操作です。素材となる推論図が（描画方向↓→なら）上段になります。では、最初の推論図はどこから持ってくるのでしょう？ “最初から在る”とみなす推論（図）を、基本推論〈primitive inference〉とか組み込み推論〈builtin inference〉と呼びます。

「シーケントとスコット・ブラケット (A10P8) // 組み込み推論を表すシーケント」に基本推論を列挙しています。

これらの基本推論には、名前が付いてます。歴史的な経緯から、ひとつの基本推論に幾つもの名前があります。例えば、プロファイルが A, A⇒B → B である基本推論は、「モーダスポネンス」、「三段論法（たぶん誤用）」、「eval（ラムダ計算から）」、「apply（ラムダ計算から）」、「ε（evalのeと、圏論の余単位から）」などと呼ばれます。

Xの恒等〈identity〉、Xの複製〈duplication〉、XとYの入れ替え〈swap〉などは、いちいち名前を書かないで、単なるワイヤー、ワイヤーの分岐、ワイヤーの交差で描きます。「スパイダーパズル (A17P10) // 汎用のスパイダー」参照。

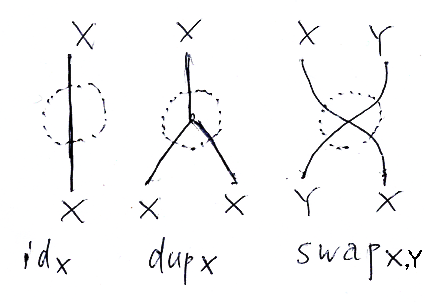
基本リーズニングの絵

単一の命題は、A, B などのラテン文字で表します。命題のリスト（連言的リスト、または選言的リスト）は、Γ, Δ などのギリシャ文字で表します。リストの項目〈要素 | 成分〉が1個の場合は、単一の命題と同一視していいので、正確に言えば：

• 単一の命題、または複数の項目を持つリストはギリシャ文字で表す。
• ギリシャ文字であっても、単一の命題かも知れない。

リストを、絵では二重線や太い線で表す人もいますが、ここでは単一の命題とリストを特に区別しないで、実線ワイヤーで描きます。

補助線、あるいは注釈線を赤で描くことにします。注釈線は、通常は省略します。ただし、

• Sumに対する注釈線（区切り線）がないと、ProdとSumの結果を区別できない。よって、Sumに対する注釈線、または注釈線に代わる何らかの目印が必要。
• Comp, Prodの注釈線（区切り線）は、なくてもよいが、ないと一意的にリーズニング図を再現することは出来なくなる。一意性を気にしないなら省略可能。
• Lambの注釈線（囲い）は、なくてもいい。

[追記]
完全に一意的な再現はやっぱり難しいなー。注釈の区切り線の長さを変えるとか、注釈として囲い枠を付けるとか、ゴチャゴチャと書き込めば一意的な再現が確かに可能ですが、そこまで注釈線を書き込むのが面倒過ぎる。
[/追記]

結合 Comp 基本リーズニング

上段の2つの推論図を縦に繋げます（あくまで、描画方向↓→での話）。左が上、右が下になります。繋いだ場所に、注釈の区切り線を横に入れます。

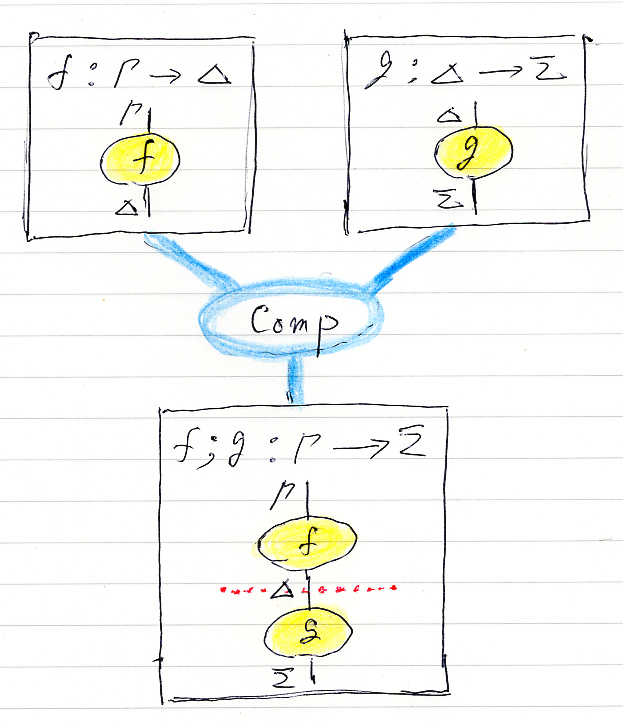
積 Prod 基本リーズニング

上段の2つの推論図を横に並べます。並べた中間に、注釈の区切り線を縦に入れます。

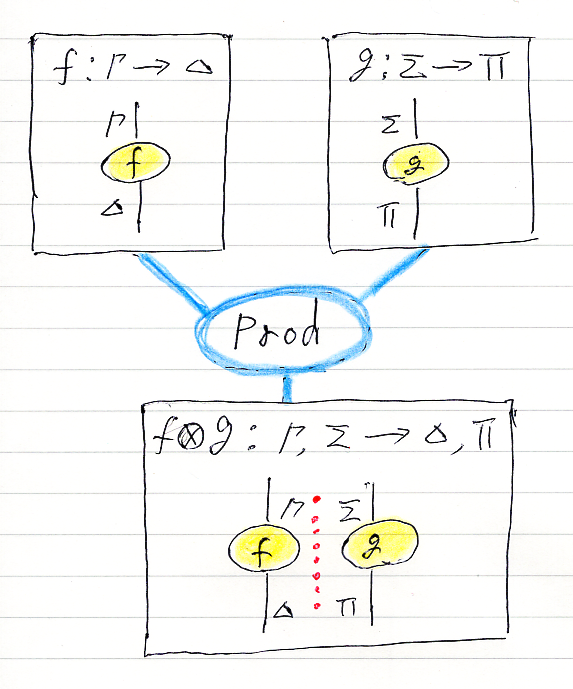
和 Sum 基本リーズニング

上段の2つの推論図を横に並べます。意味は、選言的な併置なので、積〈Prod〉とは違います。並べた中間に、注釈の区切り線を縦に実線で入れます。区切り線でなくても、積と区別するための何らかの目印が必須です。

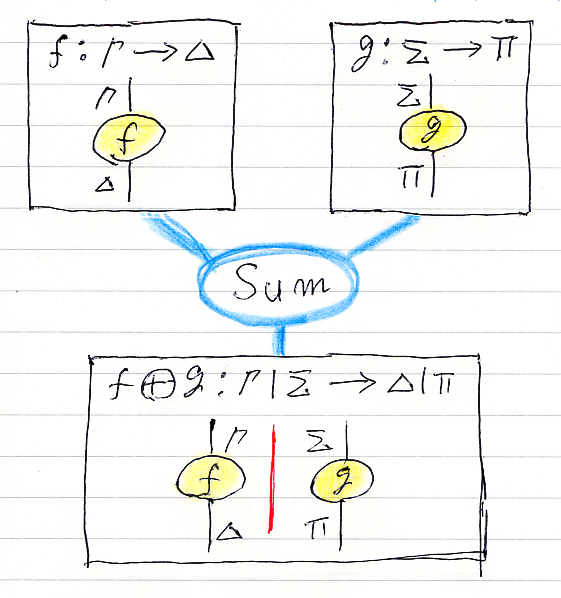
ラムダ Lamb 基本リーズニング

「Lambdaリーズニングと演繹原理〈演繹定理〉 (A20)」参照。囲いの注釈線はなくてもかまいません。とりあえず、曲げるワイヤーは一番左に限ることにします。こう制限しても、swapでワイヤーを入れ替えられるので心配は要りません。

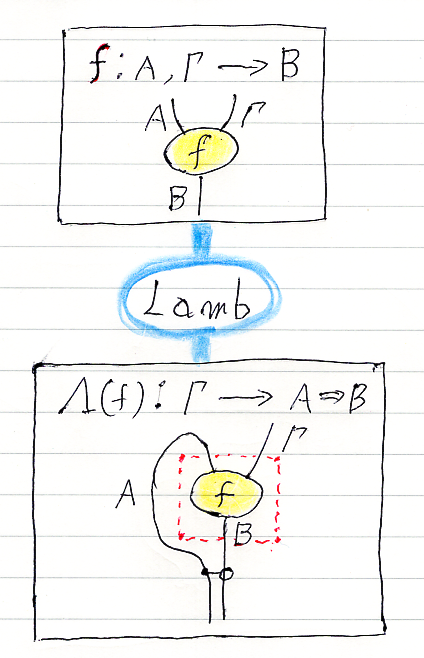
練習問題

Comp, Prod, Sum, Lamb だけしか使ってないなら、最後の推論図（出来上がり）から、構成過程であるリーズニング図が再現できます。注釈線までちゃんと描いてあれば、一意的に再現できます。

[追記]
先の追記で書いた事情で、完全に一意的な再現は難しいですね。結合律 (f;g);h = f;(g;h) の左右の違いのような差は生まれますが、それは同一視するなら、まーまー一意的です。
[/追記]

問題1： 下の推論図に対して、その構成過程であるリーズニング図を描いてください。全部乗せで、完全にグラフィカルなリーズニング図です。「全部乗せ」とは、フレーム（四角い枠）内に次を書き込むことです。

1. 推論の名前、またはテキストによる式（演算子記号を使う）
2. 推論図のプロファイル（シーケントとして書く）
3. グラフィカルな推論図

ワイヤーだけ、ワイヤーの分岐、ワイヤーの交差、ワイヤーの合流は次の記号で表します。

1. id_X
2. dup_X
3. swap_{X, Y}
4. codup_X （coは、sin, cos のcoと同じく、「相棒」を示す。）

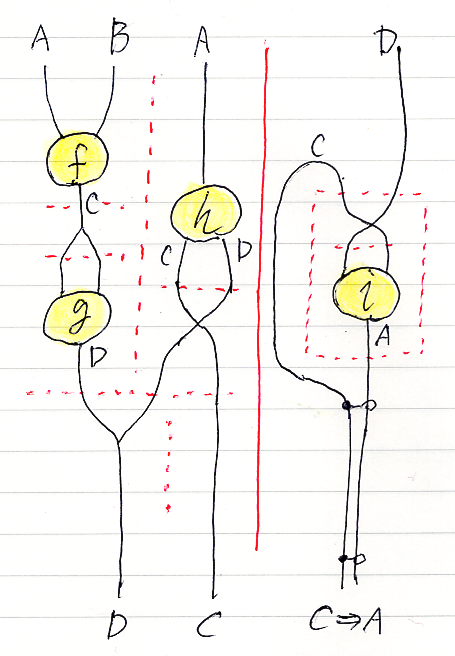
[追記]
「全部乗せで、完全にグラフィカルなリーズニング図」を描くのはムチャクチャ大変だわー。ゴメン、そこまでやんなくていいわ。真面目にやると、どの程度の労力と面積が必要かの見当がついたら、あとはテキトーに手を抜いていいです。

それと、上の図をそのままリーズニング図にすると、論理計算〈シーケント計算〉としてはちょっと具合が悪い点もありますね。解答のときに補足します。→ 解答例と修正と解説は、「問題集11「小学生でも…」の解答と補足説明 (A23R11)」
[/追記]

問題2： 完全なリーズニング図から、プロファイル（シーケント形式）だけを抜き出して、一本棒の横棒記法の図を作ってください。それが、論理の本でよくみる（例えば↓）シーケント証明図です。

*3

「ゲンツェン流のシーケント計算が分からない」理由（の多く）は、何をどう扱っているかを知らないままに省略記法だけを機械的にいじるハメになるからです。

*1:https://arxiv.org/abs/quant-ph/0510032

*2:ボブ・クック教授はミュージシャンです。

*3:画像は https://tex.stackexchange.com/questions/44582/sequent-calculus から

面積問題への対策（あるいは無策） (A21)

昨日、Lambda基本リーズニング（「含意導入規則」と呼ばれることが多い）に関して、ワイヤーベンディング描画法を説明しました。描画法を考えた当事者の意図・目的を理解しないと、「変な絵」「ワケワカメな図」になってしまいます。

描画法／記号法／表記法を考えた当事者の意図・目的で、けっこう多いのが「面積問題への対策」です。面積とは、紙面・画面の広さのことだと思ってください。グラフィカルなフル・リーズニング図は、とてもとても面積を消費するので、そのままでは描けません。そこで、より少ない面積で描ける描画法／記号法／表記法が開発されたのです。

紙のページの場合、巨大な絵の印刷は物理的に無理で、縮小すると読めなくなります。コンピュータ画面なら、スクロールやズーミング、折りたたみ／展開などにより事情は改善します。さらにアニメーションがあれば、劇的な効果があるはずです。

が、実情はツールが整備されてません。

• アニメーションとしての証明

フレーゲ（『概念記法』が1879年）に始まり、ゲンツェンのイノベーションを経た現在の論理は、よく整備されたきれいな体系になっています。にもかかわらず、適切な伝達手段（メディアとツール）がありません。貧弱な伝達手段とお粗末な手法により伝達される結果として、グチャグチャで汚い体系として受け止められる可能性があります。音響カプラを経由してYouTube動画を観ると、たぶん酷い映像になるでしょう。それと同じです（って、同じじゃない）。

悲しいかな、効果的な対策はなく、現時点で出来ることは、伝達する側も受け取る側も“根性を出す”ことだけです。手間を厭わず、広い面積の絵を何枚も提示する、自分で描いてみることです。

檜山は根性を出したくないし、根性に自信もないので、極端な面積節約は控えても、やはり手間は節約したい。

• 「アニメーションとしての証明」で言う「パラパラ漫画」方式、「紙芝居」方式で書く。
• 絵が少なめな「紙芝居」になるかも知れないが、「小説」方式（テキストのみ）にならないようには気をつける。
• 絵は、ノートに乱雑に手描きしたものをスキャンして使う。汚いけどカンベンしてね。

お約束

推論図を「全部乗せ」で描くときは、

推論図の名前またはテキストによる式 : プロファイル
（プロファイルはシーケント形式で書く）

  ここにグラフィカルな推論図
  （スパイダー＝ノード・ワイヤー図）

これは「全部乗せ」なので、名前、テキスト式、プロファイルは省略されるかも知れません。また、本体である推論図が省略されることもあります。要するに、どれも省略される可能性を持ちます。

多くの人は、一番面積をとる推論図本体を省略したがります。檜山は、他を省略しても出来るだけ本体は省略したくないと思っています。（あくまで「出来るだけ」ね。）

横棒記法に関しては：

• 原則として、推論の横棒は一本棒（'---'）、リーズニングの横棒は二本棒（'==='）。
• 両方一度に使わないときは、リーズニングでも一本棒（'---'）を使うときがある。
• 推論／リーズニングを表すラベルは、横棒の右側。ラベルも出来るだけ省略しない。（あくまで「出来るだけ」ね。）

手描きのときに一番多く使いそうな描画法は、

• 推論図はグラフィカルに（スパイダー＝ノード・ワイヤー図）として描く。
• リーズニングは横棒記法（一本棒または二本棒）として書く。

例えば（ほんとに汚えー）：

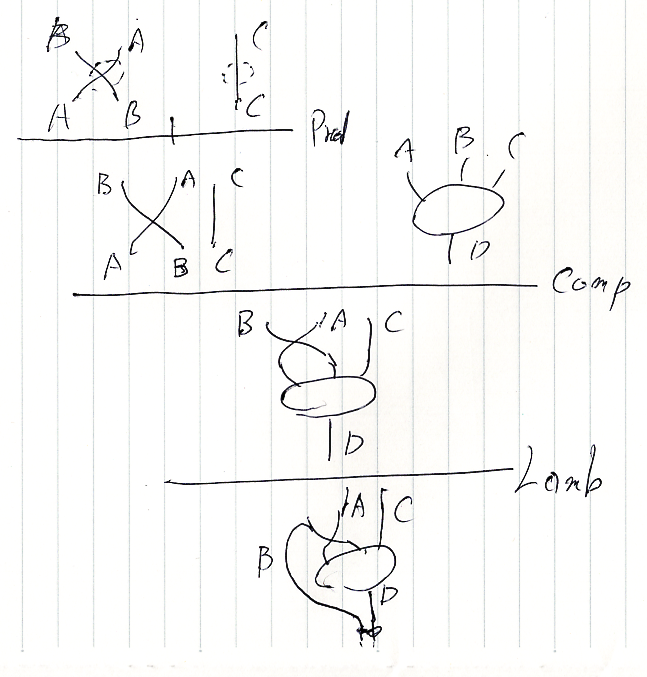
プロファイルだけ抜き出して書けば：

  B, A → A, B   C → C
 ======================= Prod
  B, A, C → A, B, C           A, B, C → D
 ============================================ Comp
      B, A, C → D
    ================= Lamb
      A, C → B⇒D

Lambdaリーズニングと演繹原理〈演繹定理〉 (A20)

Lambdaリーズニングとは、'｜'の形のワイヤーを'∩'の形にひん曲げる操作です。アンケートに「Lambdaリーズニングが分からない」とあったのですが、まー、分かりにくいでしょう。

「なんでワイヤーが曲がるのだろう？」と考えても、そりゃー分かりませんぜ。天然・自然に曲がるべき必然的理由があるとか、曲がる現象が観測できる、とかではありません*1。描画の約束事として、「ワイヤーを曲げて描こう」と人間（誰かさん）が決めたのです。なので、その約束の意図を理解する必要があります。問題は、「なぜ、あんな描き方がいいと思ったのか？」です。

内容：

1. 演繹原理〈演繹定理〉
2. フル・リーズニング図を描かないために
3. ワイヤーベンディングと留め金
4. ターンバックノードとワイヤーストレッチング

演繹原理〈演繹定理〉

演繹定理〈deduction theorem〉と呼ばれる原理があります。「定理」と呼ばれてはいますが、むしろ、演繹システムが必ず満たすべき性質、要請と捉えるべきでしょう。なので、ここでは演繹原理と呼ぶことにします（世間では「演繹定理」だけどね）。実際に定理（メタ定理）として証明（メタ証明）可能なときもあるし、演繹システムに最初から（設計段階で）この性質を組み込んでしまうこともあります。

今、A, B₁, ..., B_n （n = 1 でもよい）が仮定で、C が結論である推論Fがあったとします。スパイダー〈ノード・ワイヤー図〉で描けば下図のようです。

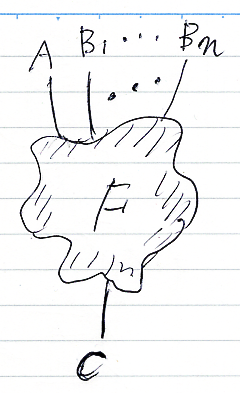
Fがグニョグニョしているのは、ものすごく複雑な推論図でも構わないからです。これは、

• A, B₁, ..., B_n から C が（推論Fで）結論できる

ということです。このことを、横書きテキストとしては、

• A, B₁, ..., B_n |-(F)→ C

と書くことにします（一時的な記法）。

A, B₁, ..., B_n |-(F)→ C という推論が認められる（やってもよい、存在する）なら、B₁, ..., B_n |-(F')→ A⇒C という推論も認めるべき、というのが演繹原理です。逆も同様なので、

• 演繹システムにおいて、A, B₁, ..., B_n |-(F)→ C という推論が認められる (⇔) B₁, ..., B_n |-(F')→ A⇒C という推論が認められる

どちらか一方だけの推論がシステム内で認められ（存在し）、もう一方は禁止されている（存在しない）なんてことがあってはいけないのです。

演繹原理に従わない演繹システムは使い物にならないことが経験上分かっているので、最初から基本リーズニング（システムに組み込みのリーズニング＝推論図の基本変形操作）に入れてしまいましょう。

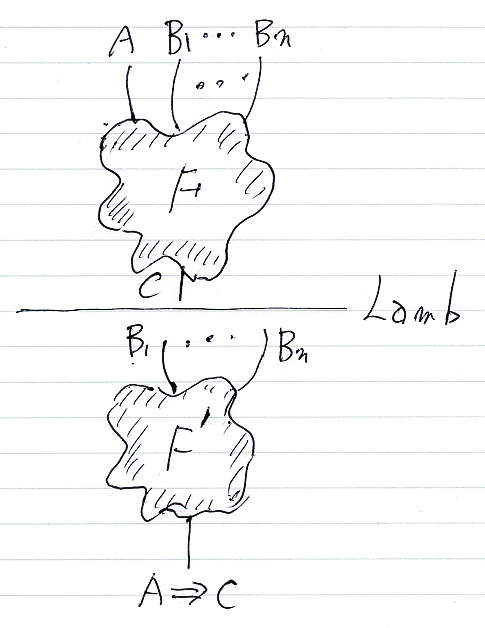
この基本リーズニングは、（カリー／ハワード対応により）ラムダ計算ではラムダ抽象に相当するので、Lambdaとネーミングしました。ネーミングで意味や機能が変わったりしません（ヒルベルトの言葉を思い出せ）。逆方向（下から上）も最初から基本リーズニングに入れてもかまいませんが、別な方法で逆向きリーズニングを有効にすることが多いかな（後述）。

今の例では、一番左のAを結論側に持ってきましたが、必ずしも左端でなくてもかまいません。例えば、

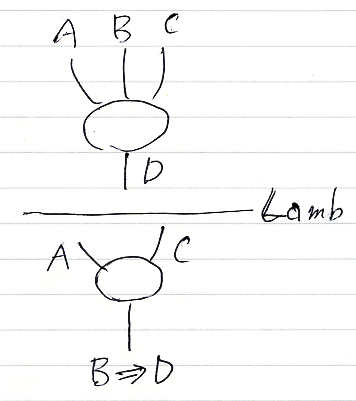
[追記]一番左にしかLambdaリーズニングを許さないとしても、ワイヤーの入れ替え（swap）操作を認めれば、入れ替えによりワイヤーを一番左に持ってこれるので、差支えはありません。[/追記]

フル・リーズニング図を描かないために

入れ子のグラフであるグラフィカルなリーズニング図をフルで描くと手間と面積がかかり過ぎます。フル・リーズニング図を描かないで済ませる工夫がいろいろされてきました。「絵図の描き方と省略法 (A16) // 省略法」にも書きましたが、基本は：

1. 最後の1枚の推論図だけで済ませる。
2. 推論図を描かずにプロファイル（シーケントとして書く）で済ませる。

ここでは、「最後の1枚」方式を考えます。ラストシーンの静止画からムービーのストーリー全体を想像せよ、ってわけです。

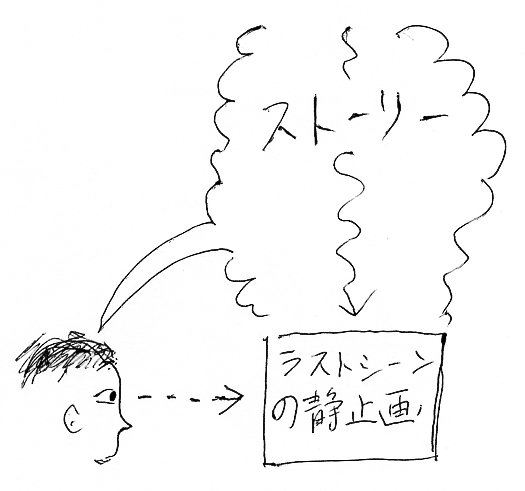
1枚の推論図に、リーズニング図を再現できるだけの情報を詰め込みます。そのためには、

• リーズニング・ステップの下段の推論図だけから、上段の推論図を再現できなくてはならない。

また、

• テキスト記法によるラベルや注釈に、できるだけ頼らない（絵だけで表現する）

ほうが望ましいです。

[追記]
現実的な話をすると、ラストシーンからムービー全体を想像するのは難しいです。ある程度練習しないと出来ないです。そして、1枚の推論図を生成するリーズニング図が一意には決まらないので、想像する人によって違ったリーズニング図が出来上がります。それら複数のリーズニング図は、同じ推論図を生成するという意味で同値なんですが、同値性の話は難しいです（面白いとも言えるが）。

それに、リーズニング図全体の情報を1枚の推論図に詰め込むので、当然ながら、ゴチャゴチャした絵になります。

そんなこんなで、僕は「最後の1枚」方式は推奨しません。「プロファイルで済ませる」方式のほうが、まだしも理解しやすいと思います。
[/追記]

さて、先の例（下に再掲）で、下段の絵だけから、しかもテキストラベルは最小にして上段の絵を再現するには、どんな絵の描き方をすればいいでしょうか？

ワイヤーベンディングと留め金

前節の問題意識で工夫・開発された描画法（絵を描くお約束）がワイヤーベンディング〈ワイヤー曲げ描画法〉です。留め金〈clasp〉を一緒に使うと直感に訴える描画が可能です。留め金を使いだしたのは、おそらく（確証はないが）ジョン・バエズ〈John Baez〉です。

下段の絵から上段の絵を再現するために、上段の絵に一切手を加えずに、そのまま下段に降ろします。しかし、上段の仮定にあったワイヤーの1本は下段で消えます。ホントに消したらダメです（再現用情報が失われる）。ワイヤーを曲げてしまえば、上段の情報を温存して、仮定（上側に突き出たワイヤー群）からは除外できます。

曲げたワイヤーは、下から出るワイヤー（上段では結論）に留め金で止めておきます。

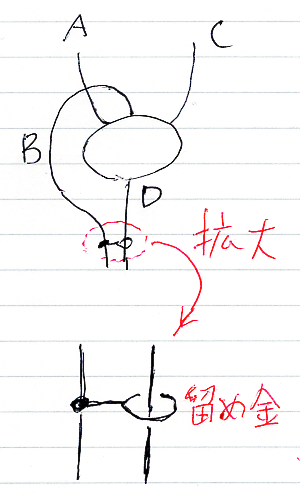
これならば、留め金を外せばすぐさま上段の絵が再現します。ワイヤーが、曲がるけど硬い、プラスチックファイバーのような素材でできてるとします。すると、留め金を外すとビヨ〜ンと戻るでしょう。

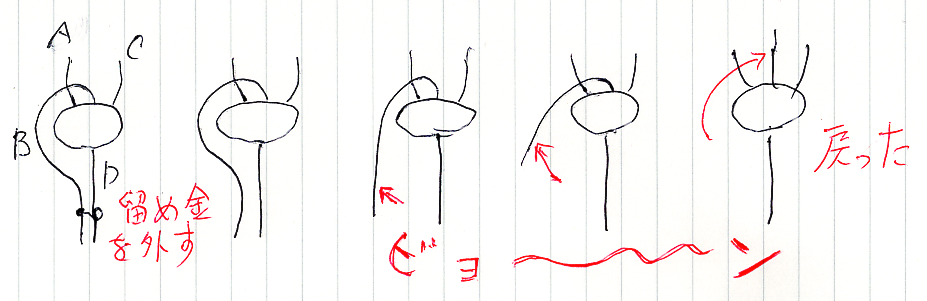
• 曲げて留め金で止める。
• 留め金を外すとビヨ〜ンと戻る。

映像的でビビッドなイメージが描けるのが、この描画法のメリットです。なお、留め金は必要に応じて何個も描きます。そうでないと、ワイヤーの併置と誤解される危険があります。

ターンバックノードとワイヤーストレッチング

留め金を外す操作を基本リーズニングに入れてもいいのですが、よく使われるのは、留め金でまとめられたワイヤーの片方をもう一度上に向かわせるターンバックノード〈turnback node〉です。

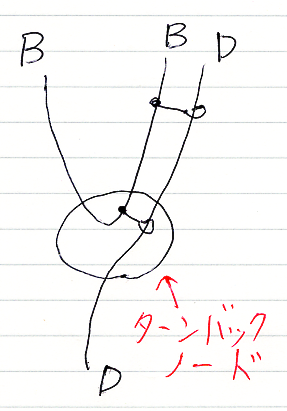
このターンバックノードは、ラムダ計算ではevalであり、論理ではモーダスポネンスになります。eval／モーダスポネンスは非常に有名な計算／推論です。古来より使われてきたeval／モーダスポネンスにより、ワイヤーを再度曲げ戻すわけです。

ラムダ抽象／演繹定理で'∩'状に曲げ、eval／モーダスポネンスで'∪'に曲げ戻すと、結局は何もしないのと同じになります。これを絵に描くと：

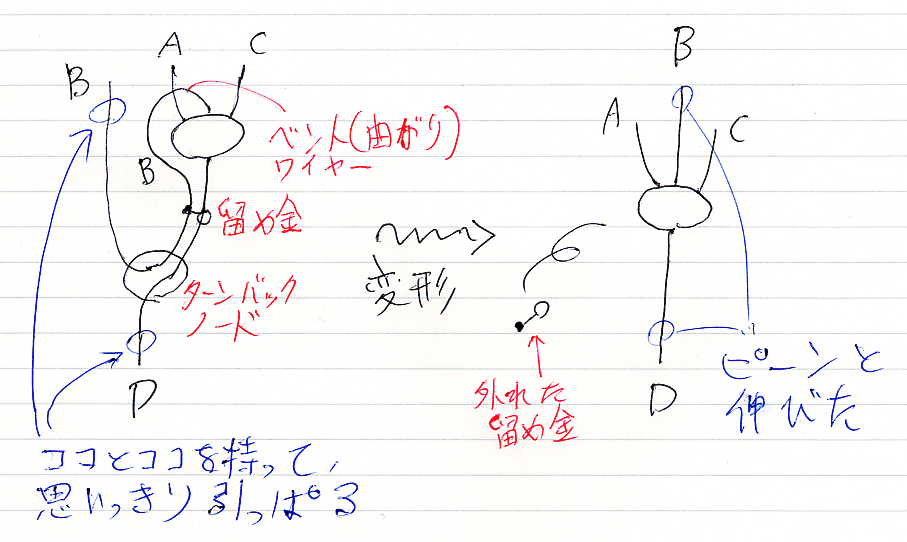
ニョロニョロに曲がったワイヤーの引き伸ばし〈ストレッチング〉は、ラムダ計算ではベータ変換〈beta reduction〉と呼ばれます。論理では推論図／リーズニング図の変形〈rewrite | move | deformation | transform〉のなかで最もポピュラーなものですが、名前はないようです。

言いたいことは、次のような推論図は無駄があるから、「∩#1 含意記号の導入」と「モーダスポネンス」は取り除いてもいい、ということです。

          #1
         ---
       A  B  C
      〜〜〜〜〜
       ナニヤラ
      〜〜〜〜〜
          C
      ---------- ∩#1 含意記号の導入
  B     B⇒C
 ---------------- モーダスポネンス
        C

ラムダ計算におけるストレッチングは、「ベータ変換」と呼ばれる次の計算規則（式の還元法）です。記号'・'がevalを表します（詳細は割愛）。

• (λx.E)・F ⇒_β E[F/x]

余談ですが、ニョロニョロを引き伸ばすという操作は、驚くほど多様な場面で登場して、双対性／随伴などの概念を統制しています。

• 本編記事から「ニョロニョロ」の検索結果： http://d.hatena.ne.jp/m-hiyama/archive?word=%A5%CB%A5%E7%A5%ED%A5%CB%A5%E7%A5%ED

紙面節約のために工夫された描画法という動機から説明したし、実際そうなんですが、「曲がったワイヤー」には、便宜的約束を超えた本質的な意味もあるようです。

---

眺めるだけでいい参考記事：

• 3年前： お絵描き証明の例
• 10年前： 紙芝居：ラムダ抽象

*1:実は、天然・自然の摂理で、あるいは数学のイデア界の法則で曲がるのかも知れません。この記事の最後の段落を参照。

定義と仕様

次のようなシーケントスタイルの定義は、

For C in Cat, D in 0Cat
For FO : C.Obj → D.Obj in Set
For FM(A, B in C.Obj) : C(A, B) → D(FO(A), FO(B)) in Set
Define
  F : C → D in Cat // F is-a-functor
  :⇔
  F = (FO, FM)
  SuchTaht
  ...
End

仕様としてまとめられる。

specification functor := {
 dom in 0Cat as C,
 cod in 0Cat as D,
 obj-part : C.Obj → C.Obj in Set as FO,
 hom-part(A, B in C) : C(A, B) → D(FO(A), FO(B)) as FH,
! laws
 ...
}

仕様と定義は同じだが、仕様のほうがモジュール化されている。

リテラチャー

リテラチャーは、セオリーのk-レイヤーの構成素 - 檜山正幸のキマイラ飼育記 メモ編で初めて出てくる概念。基本的な関係は、

• L_k = k-Lit(Σ_k+1)
• Σ_k in L_k

ここで、

1. L_kは、k次元レイヤーにいるリテラチャー
2. Σ_k+1は、(k + 1)次元レイヤーにいる特定された指標
3. k-Lit(-) は、(k + 1)-指標からk次元のリテラチャーを作り出す構成〈construction〉
4. リテラチャーとは、指標または仕様を対象とするℓ-圏。特定された指標（または仕様）は、リテラチャーから選び出す。
5. リテラチャーL_kは、ℓ-圏だが、ℓの値はハッキリしない。ℓはkに依存するかも知れないし、定数かも知れない。
6. リテラチャーは、インスティチューション用語の指標圏と同義。高次セオリー構造からインスティチューションを作るときは、リテラチャーを指標圏として使う。
7. 「アンビエントと特定されたインスタンス」の関係は「リテラチャーと特定された指標」の関係と似ている。意味論側が「アンビエント／特定インスタンス」で、構文側が「リテラチャー／特定された指標」である。
8. セオリーを指定・特定・定義するとは、すべての次元＝レイヤーに渡って、リテラチャーから指標を特定し、アンビエントからインスタンスを特定する行為をすること。
9. 次元のレイヤーと特定・生成の関係により梯子のような構造が出来る。セオリーの梯子〈ラダー〉と呼んでいいだろう。

高次射の定義の形式化

随伴に関する注意事項 - 檜山正幸のキマイラ飼育記で書いた、「構造か命題か」の問題があるので、構造としての随伴対は、adj(L -| R) と書いて、L -| R は命題として使うことにする。

ほんとは絵で描くのが良いのだが、なんとかアスキーで定義を書いてみる。ネタは、"バスケス-マルケス 2015"（https://arxiv.org/abs/1510.04724）の付録の定義群。

随伴系を対象とする2圏を 2Adj と書いて、随伴系（0-射）のあいだの射（1-射）を定義してみる。ここで：

• v⇒ ： 二重圏の2-射をストリング図で垂直方向（ペースティング図では斜め方向）に考えたもの。
• v= ： 二重圏の明示的等号である2-射（可換四角形）を垂直方向に考えたもの。
• α ←(v-inv)→β ： αとβは互いに垂直方向に逆。
• α ←(mate)→β ： αとβは互いにメイト対応している。
• L~ は、もとの論文ではオーバーライン

For L:X→C, L~:Y→D, R:C→D, R~:D→Y
Given L -| R, L~ -| R~
For J:C→D, K:X→Y, λ:: L*T v⇒ K*L~ : X→D
Given (R*K:: v= J*R~ :C→Y) ←(v-inv)→ (J*R~ v= R*K :C→Y) ←(mate)→ (λ:: L*T v⇒ K*L~ :X→D)
Define
  Ψ:adj(L -| R) → adj(L~ -| R~) in 2Adj
  :⇔
  Ψ = (J, K,λ)
End

次のように書いても同じ。

For L:X→C, L~:Y→D, R:C→D, R~:D→Y
Given L -| R, L~ -| R~
Define
  Ψ:adj(L -| R) → adj(L~ -| R~) in 2Adj
  :⇔
  Ψ = (J, K,λ)
Where
 J:C→D, K:X→Y, λ:: L*T v⇒ K*L~ : X→D
 SuchThat (R*K:: v= J*R~ :C→Y) ←(v-inv)→ (J*R~ v= R*K :C→Y) ←(mate)→ (λ:: L*T v⇒ K*L~ :X→D)
End

一応これで、随伴系のあいだの1-射 Ψ:adj(L -| R) → adj(L~ -| R~) in 2Adj は定義される。絵を描かないとピンとこないと思うが。

次に2-射 Γ::Ψ ⇒ Ψ' : adj(L -| R) → adj(L~ -| R~) in 2Adj を定義する。Ψ'の構成素は、Ψの構成素（名）にすべてダッシュを付けたやつとする。

For α::J v⇒ J':C→D, β::K v⇒ K':X→Y
Given (λ;β)*L~ = (L*β);λ' :: L*T v⇒ K'*L~ : X→D
Define
  Γ::Ψ ⇒ Ψ' : adj(L -| R) → adj(L~ -| R~) in 2Adj
  :⇔
  Γ = (α, β)
End

あるいは、

Define
  Γ::Ψ ⇒ Ψ' : adj(L -| R) → adj(L~ -| R~) in 2Adj
  :⇔
  Γ = (α, β)
Where
  α::J v⇒ J':C→D, β::K v⇒ K':X→Y
  SuchThat (λ;β)*L~ = (L*β);λ' :: L*T v⇒ K'*L~ : X→D
End

ある程度は形式化した書き方が出来る。

アイレンベルク／ムーア持ち上げとクライスリ余持ち上げ

_dRAdj_L, _dLAdj_R を随伴系の二重圏だとする。その構成素〈constituents〉は、

• 0-射は圏（または厳密2-圏の対象）
• 垂直1-射は随伴系を左関手方向で考えたもの。
• 水平1-射は関手（または厳密2-圏の射）
• 2-射は、右または左の四脚2-射

右四脚2-射、左四脚2-射というのがどうも分かりにくい。ニョロニョロ・ワイヤー（随伴系の構成素である1-射）が斜め方向だが、左斜め加群と同じ出方なら左、右斜め加群と同じ出方なら右とするか。

アイレンベルク／ムーア持ち上げと、その双対であるクライスリ余持ち上げという概念があるが、これは随伴系の二重圏の2-射の特別なものだ。自然変換が等式で与えられるもの。別な言い方をすると、ペースティング図が単なる可換図になるもの。

メイト対応で2つの二重圏を重ねて考えるとき、どちらか一方を等式的四脚2-射にできる（ある種の正規化）のだろう。二重圏のカルテットの構造は単純化するはず。

随伴系の方向反転とメイト対応という、2種の厳密対合がある。対合なので、Z₂の直積が作用している対象物になる。圏のアソシエーションとでも呼ぶべき構造かな。

単一の圏とアソシエーションの関係が面白そうだ。