このブログは、旧・はてなダイアリー「檜山正幸のキマイラ飼育記 メモ編」（http://d.hatena.ne.jp/m-hiyama-memo/）のデータを移行・保存したものであり、今後（2019年1月以降）更新の予定はありません。

今後の更新は、新しいブログ http://m-hiyama-memo.hatenablog.com/ で行います。

Lambdaリーズニングと演繹原理〈演繹定理〉 (A20)

RSS練習問題

Lambdaリーズニングとは、'｜'の形のワイヤーを'∩'の形にひん曲げる操作です。アンケートに「Lambdaリーズニングが分からない」とあったのですが、まー、分かりにくいでしょう。

「なんでワイヤーが曲がるのだろう？」と考えても、そりゃー分かりませんぜ。天然・自然に曲がるべき必然的理由があるとか、曲がる現象が観測できる、とかではありません*1。描画の約束事として、「ワイヤーを曲げて描こう」と人間（誰かさん）が決めたのです。なので、その約束の意図を理解する必要があります。問題は、「なぜ、あんな描き方がいいと思ったのか？」です。

内容：

  1. 演繹原理〈演繹定理〉
  2. フル・リーズニング図を描かないために
  3. ワイヤーベンディングと留め金
  4. ターンバックノードとワイヤーストレッチング

演繹原理〈演繹定理〉

演繹定理〈deduction theorem〉と呼ばれる原理があります。「定理」と呼ばれてはいますが、むしろ、演繹システムが必ず満たすべき性質、要請と捉えるべきでしょう。なので、ここでは演繹原理と呼ぶことにします（世間では「演繹定理」だけどね）。実際に定理（メタ定理）として証明（メタ証明）可能なときもあるし、演繹システムに最初から（設計段階で）この性質を組み込んでしまうこともあります。

今、A, B1, ..., Bn （n = 1 でもよい）が仮定で、C が結論である推論Fがあったとします。スパイダー〈ノード・ワイヤー図〉で描けば下図のようです。

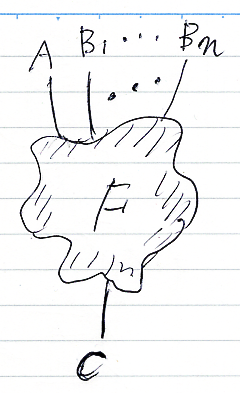
Fがグニョグニョしているのは、ものすごく複雑な推論図でも構わないからです。これは、

  • A, B1, ..., Bn から C が（推論Fで）結論できる

ということです。このことを、横書きテキストとしては、

  • A, B1, ..., Bn |-(F)→ C

と書くことにします（一時的な記法）。

A, B1, ..., Bn |-(F)→ C という推論が認められる（やってもよい、存在する）なら、B1, ..., Bn |-(F')→ A⇒C という推論も認めるべき、というのが演繹原理です。逆も同様なので、

  • 演繹システムにおいて、A, B1, ..., Bn |-(F)→ C という推論が認められる (⇔) B1, ..., Bn |-(F')→ A⇒C という推論が認められる

どちらか一方だけの推論がシステム内で認められ（存在し）、もう一方は禁止されている（存在しない）なんてことがあってはいけないのです。

演繹原理に従わない演繹システムは使い物にならないことが経験上分かっているので、最初から基本リーズニング（システムに組み込みのリーズニング＝推論図の基本変形操作）に入れてしまいましょう。

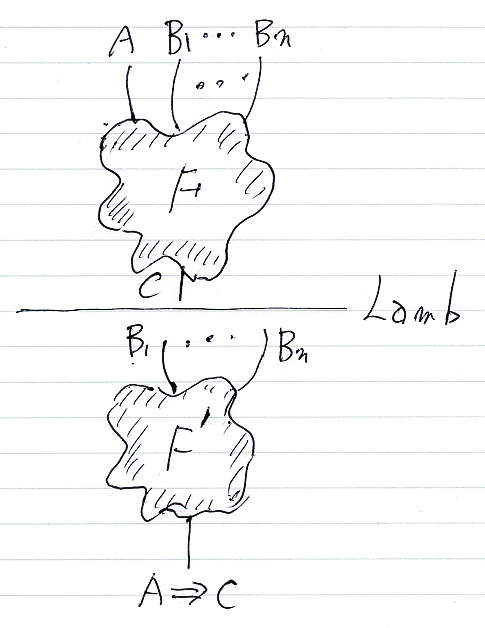
この基本リーズニングは、（カリー／ハワード対応により）ラムダ計算ではラムダ抽象に相当するので、Lambdaとネーミングしました。ネーミングで意味や機能が変わったりしません（ヒルベルトの言葉を思い出せ）。逆方向（下から上）も最初から基本リーズニングに入れてもかまいませんが、別な方法で逆向きリーズニングを有効にすることが多いかな（後述）。

今の例では、一番左のAを結論側に持ってきましたが、必ずしも左端でなくてもかまいません。例えば、

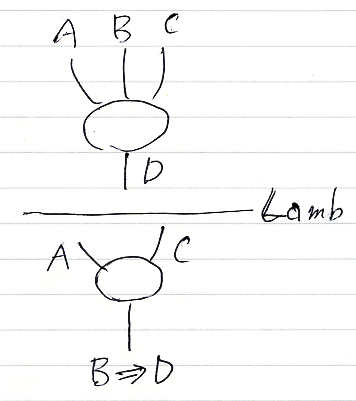
[追記]一番左にしかLambdaリーズニングを許さないとしても、ワイヤーの入れ替え（swap）操作を認めれば、入れ替えによりワイヤーを一番左に持ってこれるので、差支えはありません。[/追記]

フル・リーズニング図を描かないために

入れ子のグラフであるグラフィカルなリーズニング図をフルで描くと手間と面積がかかり過ぎます。フル・リーズニング図を描かないで済ませる工夫がいろいろされてきました。「絵図の描き方と省略法 (A16) // 省略法」にも書きましたが、基本は：

  1. 最後の1枚の推論図だけで済ませる。
  2. 推論図を描かずにプロファイル（シーケントとして書く）で済ませる。

ここでは、「最後の1枚」方式を考えます。ラストシーンの静止画からムービーのストーリー全体を想像せよ、ってわけです。

1枚の推論図に、リーズニング図を再現できるだけの情報を詰め込みます。そのためには、

  • リーズニング・ステップの下段の推論図だけから、上段の推論図を再現できなくてはならない。

また、

  • テキスト記法によるラベルや注釈に、できるだけ頼らない（絵だけで表現する）

ほうが望ましいです。

[追記]
現実的な話をすると、ラストシーンからムービー全体を想像するのは難しいです。ある程度練習しないと出来ないです。そして、1枚の推論図を生成するリーズニング図が一意には決まらないので、想像する人によって違ったリーズニング図が出来上がります。それら複数のリーズニング図は、同じ推論図を生成するという意味で同値なんですが、同値性の話は難しいです（面白いとも言えるが）。

それに、リーズニング図全体の情報を1枚の推論図に詰め込むので、当然ながら、ゴチャゴチャした絵になります。

そんなこんなで、僕は「最後の1枚」方式は推奨しません。「プロファイルで済ませる」方式のほうが、まだしも理解しやすいと思います。
[/追記]

さて、先の例（下に再掲）で、下段の絵だけから、しかもテキストラベルは最小にして上段の絵を再現するには、どんな絵の描き方をすればいいでしょうか？

ワイヤーベンディングと留め金

前節の問題意識で工夫・開発された描画法（絵を描くお約束）がワイヤーベンディング〈ワイヤー曲げ描画法〉です。留め金〈clasp〉を一緒に使うと直感に訴える描画が可能です。留め金を使いだしたのは、おそらく（確証はないが）ジョン・バエズ〈John Baez〉です。

下段の絵から上段の絵を再現するために、上段の絵に一切手を加えずに、そのまま下段に降ろします。しかし、上段の仮定にあったワイヤーの1本は下段で消えます。ホントに消したらダメです（再現用情報が失われる）。ワイヤーを曲げてしまえば、上段の情報を温存して、仮定（上側に突き出たワイヤー群）からは除外できます。

曲げたワイヤーは、下から出るワイヤー（上段では結論）に留め金で止めておきます。

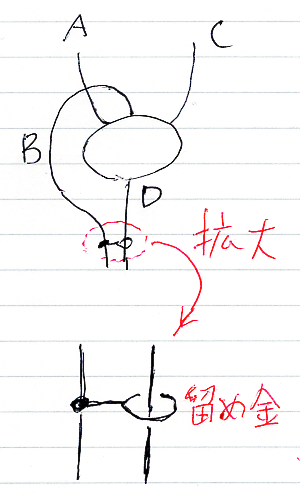
これならば、留め金を外せばすぐさま上段の絵が再現します。ワイヤーが、曲がるけど硬い、プラスチックファイバーのような素材でできてるとします。すると、留め金を外すとビヨ〜ンと戻るでしょう。


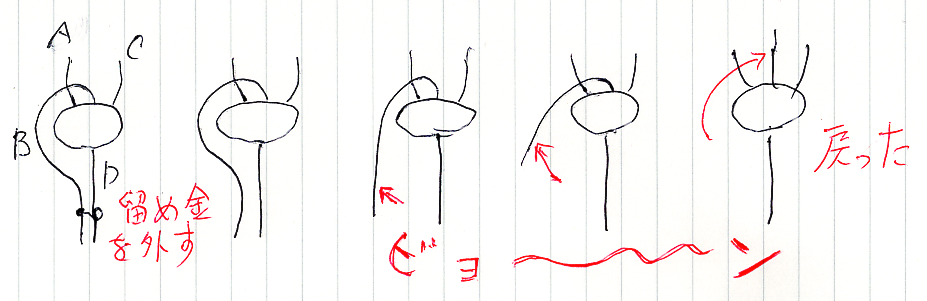
  • 曲げて留め金で止める。
  • 留め金を外すとビヨ〜ンと戻る。

映像的でビビッドなイメージが描けるのが、この描画法のメリットです。なお、留め金は必要に応じて何個も描きます。そうでないと、ワイヤーの併置と誤解される危険があります。

ターンバックノードとワイヤーストレッチング

留め金を外す操作を基本リーズニングに入れてもいいのですが、よく使われるのは、留め金でまとめられたワイヤーの片方をもう一度上に向かわせるターンバックノード〈turnback node〉です。

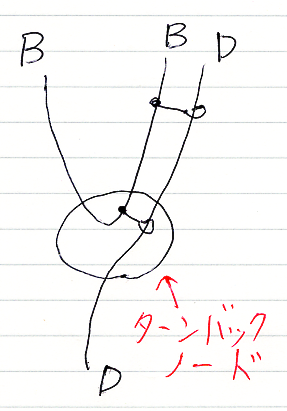
このターンバックノードは、ラムダ計算ではevalであり、論理ではモーダスポネンスになります。eval／モーダスポネンスは非常に有名な計算／推論です。古来より使われてきたeval／モーダスポネンスにより、ワイヤーを再度曲げ戻すわけです。

ラムダ抽象／演繹定理で'∩'状に曲げ、eval／モーダスポネンスで'∪'に曲げ戻すと、結局は何もしないのと同じになります。これを絵に描くと：

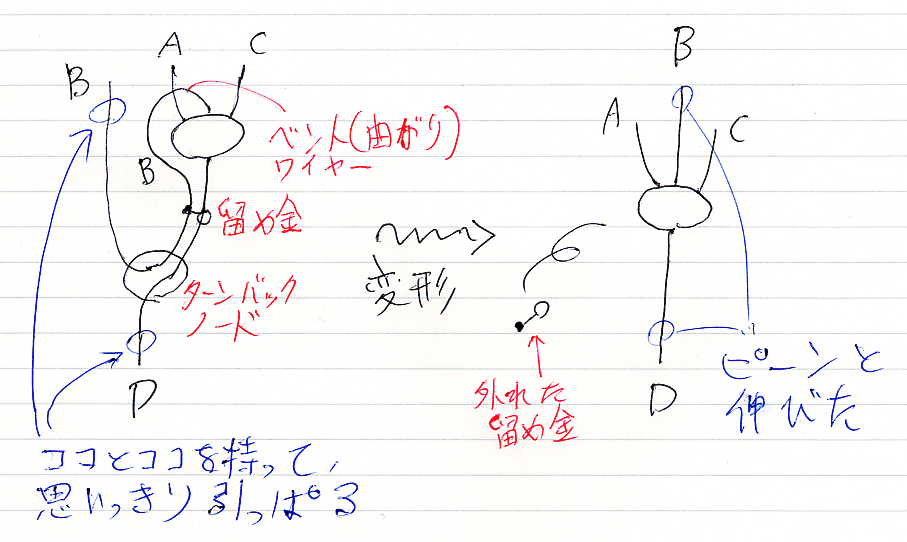
ニョロニョロに曲がったワイヤーの引き伸ばし〈ストレッチング〉は、ラムダ計算ではベータ変換〈beta reduction〉と呼ばれます。論理では推論図／リーズニング図の変形〈rewrite | move | deformation | transform〉のなかで最もポピュラーなものですが、名前はないようです。

言いたいことは、次のような推論図は無駄があるから、「∩#1 含意記号の導入」と「モーダスポネンス」は取り除いてもいい、ということです。

          #1
         ---
       A  B  C
      〜〜〜〜〜
       ナニヤラ
      〜〜〜〜〜
          C
      ---------- ∩#1 含意記号の導入
  B     B⇒C
 ---------------- モーダスポネンス
        C

ラムダ計算におけるストレッチングは、「ベータ変換」と呼ばれる次の計算規則（式の還元法）です。記号'・'がevalを表します（詳細は割愛）。

  • (λx.E)・F ⇒β E[F/x]

余談ですが、ニョロニョロを引き伸ばすという操作は、驚くほど多様な場面で登場して、双対性／随伴などの概念を統制しています。

紙面節約のために工夫された描画法という動機から説明したし、実際そうなんですが、「曲がったワイヤー」には、便宜的約束を超えた本質的な意味もあるようです。

眺めるだけでいい参考記事：

*1:実は、天然・自然の摂理で、あるいは数学のイデア界の法則で曲がるのかも知れません。この記事の最後の段落を参照。