2018-12-29

モナドの圏が17種類

モナドの圏を _σMnd_γ(K) の形で書く。σは圏のソート、γは圏の修飾子とする。

まず、修飾子は形容詞を組み合わせて作る。

形容詞記号	意味
L	左
R	右
Alg	1-射が代数的
EM	アイレンベルク／ムーア、1射が右斜め加群
Kl	クライスリ、1射が左斜め加群
S	単純、2-射が単純変換

単純変換とは限らない一般の変換＝2-射は、バイデント変換と呼ぶ。→ 弱2-圏内のモナドに関する補足：モナドが作る2-圏の多様性 - 檜山正幸のキマイラ飼育記

モナド概念を固定しても、「モナドのあいだの準同型」「モナドのあいだの準同型のあいだの準同型」という概念は一意的には決まらないようです。適用分野や目的ごとに選ぶことになるのでしょう。

ソートは、

ソート記号	意味
0	0-圏
1	1-圏
s2	厳密2-圏
ind	インデックス付き圏
coind	余インデックス付き圏

17種の一覧は次のようになる。

ソート	修飾子
0
1	LAlg, RAlg, AlgKl, AlgEM, Kl, EM
s2	AlgKl, AlgEM, SKl, SEM, SAlgKl, SAlgSE, Kl, EM
ind	L
coind	R

構成の道具として、₁Adj_L, ₁Adj_R が出てくる。

_indMnd_L in ind-Cat[₁Adj_L]
_coindMnd_R in coind-Cat[₁Adj_R]

また、1-射が左可随伴〈left-adjointable〉、右可随伴〈rightt-adjointable〉も重要な概念になる。より強く、標準的一意的に随伴の相方〈partner〉が決まっているとき、左随伴付き〈with left adjoint〉、右随伴付き〈with right adjoint〉と言う。

モナドのあいだのクライスリ準同型（左斜め加群）が、代数的とは、準同型の台1-射が右随伴付きなことである。
モナドのあいだのアイレンベルク／ムーア準同型（右斜め加群）が、代数的とは、準同型の台1-射が右随伴付きなことである。

明らかに、₁Mnd_AlgKl ⊆ ₁Mnd_Kl, ₁Mnd_AlgEM ⊆ ₁Mnd_EM 。また、

₁Mnd_AlgKl $\stackrel{\sim}{=}$ _iso ₁Mnd_AlgEM

同型関手はメイト対応（メイト転置とメイト反転置）によって与えられる。

一方、_indMnd(K)[-]:₁AdjL(K)^op→Cat は、随伴系を左関手の向きとした圏の上のインデックス付き圏である。このインデックス付き圏のグロタンディーク平坦化が ₁Mnd_LAlg(K)。

₁Mnd_LAlg(K) := Flatten(_indMnd(K)[-])

次の圏同型がある。

₁Mnd_LAlg(K) $\stackrel{\sim}{=}$ _iso ₁Mnd_AlgKl(K)

_coindMnd(K)[-] に関しても同様な同型がある。

[追記]"クリメン／ソリヴェレス 2010"（https://www.uv.es/~solivere/Articles/Kleisli%20and%20Eilenberg-Moore%20constructions%20as%20parts%20of%20biadjoint%20situations.pdf）での Mnd_alg は、monads, algebraic morphisms, and algebraic transformations の2-圏。2-圏としても定義できるが、2-射は除いて、1-圏として定義する。

インデックス付き圏、余インデックス付き圏のレベルでは、普通は2-射を考えないので、代数的準同型〈algebraic homomorphism〉は1-圏で考えれば十分だと思う。[/追記]

2018-12-29

Kock-Zöberleinの発音

リンクメモ

コック／ツーバライン

https://ja.forvo.com/search/Z%C3%B6berlein/

2018-12-28

Gurski の発音

リンクメモ

ガースキイ

https://www.youtube.com/watch?v=h3M5AMkZ1u4

2018-12-27

関手ナントカの本文記事リンク

リンクモナドセオリー論

「関手オートマトン」で検索： http://d.hatena.ne.jp/m-hiyama/searchdiary?word=%B4%D8%BC%EA%A5%AA%A1%BC%A5%C8%A5%DE%A5%C8%A5%F3
「関手データ」で検索： http://d.hatena.ne.jp/m-hiyama/searchdiary?word=%B4%D8%BC%EA%A5%C7%A1%BC%A5%BF

2018-12-20

問題集10の目的と解答と追加説明 (A19R10)

RSS練習問題

※この記事は「記事19 解答10」

問題集10とは、次の記事（の問題部分）のことです：

スパイダーパズル (A17P10)

解答だけでなく、「どうしてこのような練習をするか？」や、関連する事項の説明もします。

内容：

スパイダーパズルと演繹システム
書き方の注意
与えられたプロファイルのスパイダーを構成する
構成不可能性定理 1
構成不可能性定理 2
構成可能性定理

スパイダーパズルと演繹システム

「スパイダーパズル (A17P10)」で次のように言いました。

この記事の問題をやれば、形式化された証明や演繹システムに対して、（詳細はともかくとして）かなりの程度のイメージが持てると思います。

スパイダーパズルは、人間がルールを決めて作ったパズル（ゲーム）です。演繹システムも、人間がルールを決めて作ったパズル（ゲーム）システムです。目的や複雑さが違うだけで、メカニズムは同じです。同列に論じてかまいません。

スパイダーパズルを実際に解いたり（プロファイルに対するスパイダーを構成したり）、スパイダーパズルのシステムとしての特性を証明したりすると、次のことが実感として分かるでしょう。

パズルのシステムは、人間が恣意的に作った人工的システムである。作り方の自由度が高く、色々なバリエーションがあり得る。
パズルのシステムを調べる際に、特別な予備知識は要らない。
パズルのシステムを調べる際に、特別に難しい議論をすることはない。
だが、長く煩雑な、ときに退屈な議論を続けることはある。技量も瞬発力も必要ないが、地味な持久力が要求される。

演繹システムに対しても、同じことが言えます。なぜなら、演繹システムも、人間がルールを決めて作ったパズル（ゲーム）システムだからです。

書き方の注意

次の書き方の約束は、あまり（ほとんどかも）使っていません。

メタ論理（形式されてない通常の論理）の論理記号は丸括弧で囲む。(∧), (⇒) など。
形式化された命題である論理式は引用符で囲む。"∀x∈R.∃y∈R.(y² = x)" のように。

形式化されている／されてないを特に強調したいときは、気まぐれに使います。

与えられたプロファイルのスパイダーを構成する

構成できる／できないを先に言うと：

B, A → A ○
B, A → B ×
B, A → C ○
A → A, B ×
B → A, B ○
C → A, B ×
C, C, B → A, A ○
B, B → A, A ○

構成可能なスパイダーにはその構成図を示します。構成図の最下段にテキスト表現も添えます。×印のプロファイルを持つスパイダーが構成できないことは、後で述べる構成不可能性定理から言えます。

※注意：二本棒横棒の区切りをハッキリさせる目的で'+'を入れているところがあります。が、いつでも入っているわけではありません。後で出てくる、上段にあるスパイダーの個数が未定の構成図のときは、'+'をうまく入れることが出来ません。

B, A → A

   ☆           ☆
 ====== Ent   ======== Ent
  B  A         A  B
 ----- swap   ------ a
  A  B          A
 ===========+=========== Comp
          B  A
         ------ swap
          A  B
          ---- a
           A
 swap;a

B, A → C

  ☆            ☆
 ===== Ent    ====== Ent
  B  A         A  B
 ----- swap   ----- c
  A  B          C
 ==========+========== Comp
         B  A
        ------ swap
         A  B
        ------ c
          C
 swap;c

B → A, B

   ☆           ☆
 ====== Ent  ======= Ent
   B          B  A
 ----- b     ------ swap
  B  A        A  B
 ===========+=========== Comp
            B
         ------ b
          B  A
         ------ swap
          A  B
 b;swap

C, C, B → A, A



   ☆         ☆

 ====== Ent  ====== Ent

   C           C

  --- d       --- d

   A           A              ☆

 =========+========== Prod ====== Ent

       C    C                B

      ---d ---d             ---- id

       A    A                B             別記

 ======================+=========== Prod  〜〜〜〜

                    C   C   B             A  A  B

                   --d --d --id          --------- F

                    A   A   B              A  A

                  ===================+=============== Comp

                    C   C   B

                   --d --d --id

                    A   A   B

                   ---------- F

                      A  A

 (ddid_B);F
別記部分
  ☆          ☆

 ===== Ent  ======= Ent

   A         A  B

  --- id     ----- a

   A           A

 ==========+============ Prod

        A      A  B

 F :=  --- id ------ a

        A       A
 F := id_Aa

B, B → A, A



    別記           別記

  〜〜〜〜〜    〜〜〜〜〜

     B              B

    --- F          --- F

     A              A

   ===========+=========== Prod

          B     B

         ---F ---F

          A    A

 FF
別記部分
    ☆          ☆

  ======= Ent ======= Ent

     B         B  A

   ----- b    ------ swap

   B  A        A  B

  =========+========= Comp

           B                     ☆

         ----- b             ========== Ent

          B  A                 A  B

         ----- swap           ------ a

          A  B                   A

        ================+================ Comp

                        B

                      ----- b

                       B  A

              F :=    ----- swap

                       A  B

                      ----- a

                         A

 F :=  b;swap;a

構成不可能性定理 1

目的とする命題（非形式的な、自然言語で書かれた命題）は次です。

形が Γ → B であるプロファイルに対して、スパイダーは構成できない。ただし、Γは、A, B, C からなるリストで、B（単一のB）ではない。

スパイダー構成図を「上から見ていく方法」と「下から見ていく方法」の二種で証明してみます。この二種は、実質は同じことです。共通に使う補題があるので、それを先に示します。

共通の補題

スパイダー〈ノード・ワイヤー図 | ストリング図〉Fに関する次の条件を考える。

[条件ア] スパイダーFのプロファイルが Γ → B であり、ΓはBではない。

スパイダー F, G, H に関する次の構成図（のワンステップ）を考える。

  F   G
 ===+=== Comp
    H

このとき、次が成立する。

[補題] Hが条件アを満たすなら、FかGの少なくとも一方は条件アを満たす。

対偶をとれば、

[補題の対偶] FとGのどちらも条件アを満たさないなら、Hも条件アを満たさない。

では、補題を示す。Hは条件アを満たすとして、スパイダーにプロファイルを添えた構成図を描く。

  F:Γ→Δ   G:Δ→B
 ==========+========== Comp
        H:Γ→B

Δの形により場合分けして：

Δ = B 、つまり Gのプロファイルは B → B 。
Δ = B ではない。

場合1なら、F:Γ→B が条件アを満たす。場合2なら、G：Δ→B が条件アを満たす。オワリ。

上から見ていく方法

補題で出した条件アは引き続き参照する。

スパイダー構成図の最上段は☆である。☆に対して使用できる操作は次のいずれかである。

id, dup, swap を具体化してのEnt
a, b, c, d のEnt

それぞれの場合について：

id_B のプロファイルは B → B だが、この形は条件から除外されているので、「id, dup, swap のEnt」からは、条件アを満たすスパイダーは得られない。
「a, b, c, d のEnt」からも、条件アを満たすスパイダーは得られない。

最上段以外で登場する操作は次のいずれかである。

Prod
Comp

それぞれの場合について：

Prodにより得られたスパイダーのプロファイルの右辺リストは、長さ2以上となるので、上段が何であれ、条件アを満たすスパイダーは得られない。
補題の対偶より、Comp構成の上段のどちらも条件アを満たさないなら下段も条件アを満たさない。

以上より、どのようなスパイダー構成図でも、条件アを満たすスパイダーは出現しない。よって、条件アを満たすスパイダーは構成できない。オワリ。

下から見ていく方法

条件アを満たすスパイダーが結果（最下段）となるスパイダー構成図が存在すると仮定する（背理法の仮定）。結果を得るために使用した操作は次のいずれかである。

id, dup, swap を具体化してのEnt
a, b, c, d のEnt
Prod
Comp

それぞれの場合について（詳細は「上から見ていく方法」）：

条件アを満たすスパイダーは得られない。
条件アを満たすスパイダーは得られない。
条件アを満たすスパイダーは得られない。

したがって、結果（最下段の条件アを満たすスパイダー）は、Compによって作られる。補題より、上段左か、上段右は条件アを満たすスパイダーである。

今、上段から条件アを満たすスパイダーを選ぶ。同じ考察により、その上段から、条件アを満たすスパイダーを選ぶ。この選択は無限に行えるので、構成図は無限の高さ（上下方向のサイズ）を持つことになる。

しかし、実際は構成図は有限の高さだから、条件アを満たすスパイダーが結果となるスパイダー構成図は実は存在しない。よって、条件アを満たすスパイダーは構成できない。オワリ。

構成不可能性定理 2

目的とする命題（非形式的な、自然言語で書かれた命題）は次です。

プロファイルの形が Γ → Δ で、リストΓ内にBが出現せず、リストΔ内にBが出現するとき、このプロファイルに対してスパイダーは構成できない。

スパイダー〈ノード・ワイヤー図 | ストリング図〉Fに関する次の条件を考えます。

[条件イ] スパイダーFのプロファイルが Γ → Δ であり、リストΓ内にBが出現せず、リストΔ内にBが出現する。

条件イの否定を条件ウとします。

[条件ウ] スパイダーFのプロファイルが Γ → Δ であり、リストΔ内にBが出現するなら、リストΓ内にもBが出現する。

条件ウが条件イの否定であることがピンとこない人は、すぐ下の補足を参照してください。

[補足]

リストΓ内にBが出現することを、"B occurs in Γ" から bocc(Γ) と書くことにします。また、論理記号 (∧), (∨), (⇒), (¬) を使います。これは、記述を短縮する目的だけで、形式化した演繹システム内で考えるわけではありません。あくまで、非形式的な通常証明のなかで、短縮した記号的表現を使うだけです。別な言い方をすると；これを書いている檜山は、現実世界の人間どうしのコミュニケーションを目的として書いています。

条件イの主張は、

(¬)bocc(Γ) (∧) bocc(Δ)

これを否定すると、

(¬)( (¬)bocc(Γ) (∧) bocc(Δ) )

通常我々が現実世界で使っているド・モルガンの法則から、

bocc(Γ) (∨) (¬)bocc(Δ)

(∨)の左右を入れ替えてもいいから、

(¬)bocc(Δ) (∨) bocc(Γ)

通常我々が現実世界で使っている古典論理では、これは含意を意味するので、

bocc(Δ) (⇒) bocc(Γ)

つまり、

リストΔ内にBが出現するなら、リストΓ内にもBが出現する。

[/補足]

任意のスパイダー構成図が次の性質を持つことを示すことにします。

[性質エ] スパイダー構成図に出現するすべてのスパイダーは、条件ウを満たす。

スパイダー構成図に関する“構造帰納法”を用いて証明します。準備として、結果（最下段）をひとつ持つスパイダー構成図を場合分けします。

スパイダー構成図がノード（構成ステップ）をひとつしか持たず、それが「id, dup, swap を具体化してのEnt」の場合
スパイダー構成図がノード（構成ステップ）をひとつしか持たず、それが「a, b, c, d のEnt」の場合
スパイダー構成図の最後のノード（構成ステップ）がProdの場合
スパイダー構成図の最後のノード（構成ステップ）がCompの場合

場合1

さらに、id, dup, swap で場合分けする。X, Yは、A, B, C のどれかを表す。

      ☆
    ======= Ent
       X
F =   --- id
       X

このとき、下段のスパイダーFに関して、

出力列にBが出現する (⇒) 入力列にBが出現する

なので、条件ウを満たす。

       ☆
    ========= Ent
       X
F =  ----- dup
      X  X

このとき、下段のスパイダーFに関して、

出力列にBが出現する (⇒) 入力列にBが出現する

なので、条件ウを満たす。

        ☆
    =========== Ent
       X  Y
F =   ------ swap
       Y  X

このとき、下段のスパイダーFに関して、

出力列にBが出現する (⇒) 入力列にBが出現する

なので、条件ウを満たす。

場合2

さらに、a, b, c, d で場合分けする。

       ☆
    ========== Ent
      A  B
F =  ------ a
       A

このとき、下段のスパイダーFに関して、出力列にBは出現しないので、

出力列にBが出現する (⇒) 入力列にBが出現する

は成立して、条件ウを満たす。

       ☆
    ========== Ent
       B
F =  ------ b
      B  A

このとき、下段のスパイダーFに関して、

出力列にBが出現する (⇒) 入力列にBが出現する

なので、条件ウを満たす。

       ☆
    ========== Ent
      A  B
F =  ------ c
       C

このとき、下段のスパイダーFに関して、出力列にBは出現しないので、

出力列にBが出現する (⇒) 入力列にBが出現する

は成立して、条件ウを満たす。

       ☆
    ========== Ent
       C
F =  ----- d
       A

このとき、下段のスパイダーFに関して、出力列にBは出現しないので、

出力列にBが出現する (⇒) 入力列にBが出現する

は成立して、条件ウを満たす。

場合3

スパイダー構成図の最後のノード（構成ステップ）がProdなので、



   F:Γ→Δ   G:Σ→Π

  ==========+========== Prod 最後のノード

    FG:Γ Σ → Δ Π

下段の出力列にBが出現するには、

ΔにBが出現する
ΠにBが出現する

の少なくとも一方が成立している。

上段のF, Gが条件ウを満たすなら、

ΓにBが出現する
ΣにBが出現する

の少なくとも一方が成立している。

これらより、下段の入力列 Γ Σ にBが出現するから、スパイダー F $\otimes$ G は次（条件ウ）を満たす。

出力列にBが出現する (⇒) 入力列にBが出現する

Prod構成ノードにおいて、

上段のスパイダーが条件ウを満たすなら、下段のスパイダーも条件ウを満たす。

場合4

スパイダー構成図の最後のノード（構成ステップ）がCompなので、



   F:Γ→Δ   G:Δ→Σ

  ==========+========== Comp 最後のノード

      F;G:Γ → Σ

下段の出力列にBが出現するには、

ΣにBが出現する

上段のGが条件ウを満たすなら、

ΔにBが出現する

上段のFが条件ウを満たすなら、

ΓにBが出現する

これらより、下段の入力列ΓにBが出現する。つまり、スパイダー F;G は次（条件ウ）を満たす。

出力列にBが出現する (⇒) 入力列にBが出現する

Comp構成ノードにおいて、

上段のスパイダーが条件ウを満たすなら、下段のスパイダーも条件ウを満たす。

総括

任意のスパイダー構成図が与えられたとき、場合1と場合2の考察から、☆の直下のスパイダーは条件ウを満たす。場合3と場合4の考察から、上段が条件ウを満たすなら、下段もまた条件ウを満たす。したがって、スパイダー構成図に出現するすべてのスパイダーは条件ウを満たす。言い方を換えると、任意のスパイダー構成図は性質エを満たす。

[性質エ] スパイダー構成図に出現するすべてのスパイダーは、条件ウを満たす。

特に、結果（最下段）のスパイダーも条件ウを満たす。よって、条件ウを満たさないスパイダー（条件イを満たすスパイダー）を構成することは出来ない。

構成可能性定理

目的とする命題（非形式的な、自然言語で書かれた命題）は次です。

プロファイルの形が B → Δ で、ΔはAとCから構成されるリスト（非空でBは含まないリスト）のとき、このプロファイルに対してスパイダーは構成できる。

幾つかの準備が必要です。まず、この節で使う F, G は特定のスパイダーを表す固有名詞です。

         B
       ------ b
        B  A
 F :=  ------ swap
        A  B
       ------ a
         A


         B
       ------ b
        B  A
 G :=  ------ swap
        A  B
       ------ c
          C

F:B→A, G:B→C で、FもGも構成可能です（構成図は各自描いてみてください）。

次に、整数 2, 3, 4, ... で番号付けられたスパイダー達 H_n を定義します。

H₂ := dup_B : B → B, B
H_n+1 := dup_B;(id_B $\otimes$ H_n) : B → B, B, ..., B （右辺は(n +1)個のB）

H₂は明らかに構成可能で、H_nが構成可能ならH_n+1が構成可能なのは、次の構成図から分かります。



   ☆            別記部分

 ======= Ent    〜〜〜〜〜〜〜〜〜〜〜〜〜

    B             B  B

  ----- dup      --------------- id_BH_n

   B  B           B, B, ..., B （(n+1)個）

 ============+================================== Comp

    dup_B;(id_BH_n): B → B, B, ..., B （(n+1)個）
別記部分
  ☆          H_n の構成図

 ===== Ent  〜〜〜〜〜〜〜〜〜〜〜〜〜

   B              B

  --- id     --------------- H_n

   B          B, ..., B （n個）

 ========+=========================== Prod

   id_BH_n : B, B → B, B, ..., B （(n +1)個）

また、n個のスパイダー（n ≧ 2）から1個のスパイダーを構成する操作（構成法）として、Prod_nを定義しましょう。K₁, ..., K_n が任意のn個のスパイダーだとして、



  K₁ ・・・ K_n

 ============== Prod_n

  K₁...K_n

Prod_nからProd_n+1を構成するには、



  K₁ ・・・ K_n

 ============== Prod_n

  K₁...K_n  K_n+1

 ================== Prod

 (K₁...K_n)K_n+1

Prod₃, Prod₄ などが構成図内に出現したら、それは長い構成図の略記と思えばいいのです。（構文的マクロ展開をご存知に方は、マクロ展開だと理解してください。）構成図にProd_nが出現しても、それを長い構成図に置き換えて消去することが出来るので、Prod_nを使用しても使用しなくても、スパイダーの構成可能性に影響はありません。

ΔがAとCから構成される長さnのリストだとして、B→Δ をプロファイルに持つスパイダーの構成法を以下に述べます。

n個のスパイダー K₁, ..., K_n を次のように定義する。

リストΔのi番目の項目がAのとき、K_i = F とする。
リストΔのi番目の項目がCのとき、K_i = G とする。

K_iはFかGのどちらかで、FもGも構成可能なので、次のような構成図を作れる。



   ここにナニヤラカニヤラ

   〜〜〜〜〜〜〜

    K₁ ・・・ K_n

H_nも構成可能だったので、Prod_nを使って次の構成図を作れる。



           〜〜〜〜〜〜〜

           K₁ ・・・ K_n

 〜〜     =============== Prod_n

  H_n        K₁...K_n

 ======================= Comp

    H_n;(K₁...K_n)

H_n:B → B, ..., B（n個）、 (K₁ $\otimes$ ... $\otimes$ K_n):B, ..., B（n個） → Δ なので、これらを結合したスパイダーのプロファイルは B → Δ となる。オワリ。

2018-12-19

スパイダーの構成不可能性定理を変更 (A18)

RSS練習問題

当初（2018-12-18）、「スパイダーパズル (A17P10)」において、「次の定理を証明せよ」という問題を出しました。

構成不可能性定理：プロファイルの形が Γ → Δ で、リストΓ内に出現するBの個数が、リストΔ内に出現するBの個数より少ないとき、このプロファイルに対してスパイダーは構成できない。

この構成不可能性定理を出したのは、以下のプロファイルを持つスパイダーが構成不可能であることを示すことが目的です。

A → A, B
C → A, B

しかし、上記の定理（定理じゃないが）は、反例があって、B → B, B というプロファイルを持つスパイダーは構成できます。

     ☆
  ========= Ent
     B
   ------ dup
    B  B

間違いました。次のように変更します。

構成不可能性定理：プロファイルの形が Γ → Δ で、リストΓ内にBが出現せず、リストΔ内にBが出現するとき、このプロファイルに対してスパイダーは構成できない。

2018-12-18

スパイダーパズル (A17P10)

RSS練習問題

※この記事は「記事17 問題集10」

この記事の問題をやれば、形式化された証明や演繹システムに対して、（詳細はともかくとして）かなりの程度のイメージが持てると思います。問題の解答例は、早めに（たぶん次回）出す予定です。[追記]解答はこちら → 問題集10の目的と解答と追加説明 (A19R10)[/追記]

内容：

必要な知識とスキル
ノード・ワイヤー図のプロファイル
スパイダー
汎用のスパイダー
スパイダーの構成問題
構成可能性／構成不可能性定理
スパイダーパズル

必要な知識とスキル

ノード・ワイヤー図〈ストリング図〉について知っている必要があります（次の記事）。

ノード・ワイヤー図〈ストリング図〉 (A1)

ノード・ワイヤー図の実例や操作にある程度は慣れている必要があります。次の練習問題はやっている（やったことにより獲得できるスキルを持っている）と仮定します。

次の練習問題もやってあると望ましいです。（必須とは言わないが。）

以下もやってあれば、申し分ないです。

単純式の操作の操作 (A5P4)

ノード・ワイヤー図のプロファイル

ノード・ワイヤー図〈ストリング図〉は、↓→の描画方向で描くとして、一番上に現れるワイヤーラベルの並び〈リスト〉を入力列と呼びます。同様に、一番下に現れるワイヤーラベルの並びを出力列と呼びます。そして、「カンマで区切った入力列 → カンマで区切った出力列」という形を、ノード・ワイヤー図のプロファイル〈profile〉と呼びます。

形の上では、プロファイルはシーケントと同じ形になります。実際、シーケントはプロファイルとしても使われるのですが、今回は、シーケントを忘れても（知らなくても、思い出さなくても）いいです。

次の図（「ノード・ワイヤー図〈ストリング図〉 (A1)」で出した図）のプロファイルは、A, X → C, Y です。

  A
 ---f
  B    X
 ---g ---u
  C    Y

次の図（「整数式の構文解析木 (A4P3)」で出した図）のプロファイルは、x, y → yy + xx です。

   x           y
 ----- dup   ----- dup
  x  x        y  y
 ------ prod ------ prod
   xx         yy
  --------------- swap
   yy    xx
  ---------- sum
   yy + xx

ノード・ワイヤー図のワイヤーラベルはいくらでも複雑になりえます。ラベルが再び絵図になることもあります。例えば、「問題集1の目的と解答と追加説明重要！ (A13R1)」で出した次のノード・ワイヤー図（の横棒記法による表現）がその例です。

              ☆
            ====== Ent
             A  B       A∧B
             ----γ    -----
   ☆        A∧B        C
 ====== Ent ================= Comp
  B  A          A  B
  ----σ        -----
  A  B           C
 ===================== Comp
         B  A
        -----
          C
      ========= Lamb
          A
        ------
         B⇒C
      ========= Ins(up 1, T)
         A T
        ------
         B⇒C
      ========= Lamb
          T
       ---------
       A⇒(B⇒C)

こういう図のプロファイルは、1行のテキストではどうにもならないので、例えば、

         A∧B             T
☆, ☆, ------ ＝＝＞ ---------
          C           A⇒(B⇒C)

繰り返し言いますが、テキストでは表現しにくいものを無理にテキストで表現しようとすることで、（無駄な）難解さが生み出されています。それは承知の上で、無理に書けば：

上の図のプロファイルは、 ☆, ☆, (A∧B → C) =▷ (T → A⇒(B⇒C))

※注意：星（☆）は、何もないことを表すマーカーなので、通常は星を省略して、(A∧B → C) =▷ (T → A⇒(B⇒C)) をプロファイルとします。

矢印が三種類も出てきています。

'⇒' は、含意を表す論理記号
'→' は、横棒の上下を左右で表すための矢印
'=▷' は、プロファイルにおける入力列と出力例を区切る矢印

論理では、ほんとにイッパイ矢印が出てきます。興味があれば本編記事：

論理におけるさまざまな「矢印」達

さて次は、「問題集1の目的と解答と追加説明重要！ (A13R1)」で出した、連立方程式を解く過程の図（省略部分あり）。

         2x - 3y + 1 = x - 2
         x + y = 5
       ---------------------- Ins(-x - 1)
         2x - 3y + 1 = x - 2
         x + y = 5
         -x - 1 = -x - 1
       -------------------- Add(#1,#3)
         x - 3y = -3
         x +  y =  5
         -x - 1 = -x - 1
  ---------------------------------- Fork
   x - 3y = -3       x - 3y = -3
   x +  y =  5       x +  y =  5
   -x - 1 = -x - 1   -x - 1 = -x - 1
  〜〜〜〜〜〜〜〜   〜〜〜〜〜〜〜〜〜
  〜〜〜〜〜〜〜〜   〜〜〜〜〜〜〜〜〜
    x = 3             y = 2
   -------------------------- Merge
            x = 3
            y = 2

これのプロファイルは、次のように書けば伝わるでしょう。

上の図のプロファイルは、 {2x - 3y + 1 = x - 2, x + y = 5} → {x = 3, y = 2}

今まで出たプロファイルの書き方は、色々です。



A, X → C, Y
x, y → yy + xx
         A∧B             T

☆, ☆, ------ ＝＝＞ ---------

          C           A⇒(B⇒C)
☆, ☆, (A∧B → C) =▷ (T → A⇒(B⇒C))
{2x - 3y + 1 = x - 2, x + y = 5} → {x = 3, y = 2}

書き方というものは（困ったことには）、歴史的経緯とかその他諸々の事情で、根拠も節操もなく多様化（膨大な方言が発生）してしまいます。そのような無駄な多様性／迷惑な多様性に慣れる必要があります。記号に振り回されるのではなくて、記号を操る立場になりましょう。次の記事にトレーニング用問題があります。

基本スキルの確認と練習 (A6P5)

スパイダー

ノード・ワイヤー図のノードのことをスパイダー〈spider〉とも呼びます。ノードとスパイダーは完全に同義語です。あえて同義語を新しく導入するにはいくつかの理由があります。

「ノード」というと、グラフ理論におけるグラフのノードのように、ワイヤー（辺）から切り離した単なる点としても存在できる印象がありますが、そうではありません。ノード・ワイヤー図のノードは、ワイヤー（の一部）と分離不可能です。点やアイコンというよりは、電子デバイスを思い浮かべてください。

電子デバイスには脚が生えており、脚もデバイスの一部です。脚がないデバイスはどことも接続できません。同様に、ノード・ワイヤー図のノードには、入るワイヤーと出るワイヤーが脚としてくっついているのです。このことを強調するために、ノードをスパイダーとも呼ぶことにします。蜘蛛〈スパイダー〉の脚をもぎ取ったら死んでしまうでしょう、そんな可哀想なことをしてはいけません！

実は、用語「スパイダー」は用語「ノード・ワイヤー図」とも同義です。奇妙に感じるでしょうが。

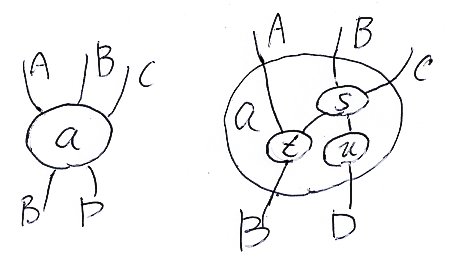
図の左のようなスパイダー a があったとします。そのプロファイルは A, B, C → B, D です。しかし、a は実際はクラスターであり、図の右のように、内部に s, t, u が入っているとします。右側は、全体として名前'a'で識別されるノード・ワイヤー図です。

ノードは、それ以上は分解できない〈原子的 | 基本 | 原始的 | アトミック | プリミティブ〉ノードとは限りません。他のノード達から構成されるクラスターかも知れません。よって、「ノード」「クラスター」「ノード・ワイヤー図」をちゃんと区別するのは不可能なのです。

用語「スパイダー」は、「ノード」「クラスター」「ノード・ワイヤー図」のどれの意味でも使用し（もともと区別がないんだし）、特に分解不可能（と想定する）ならば基本スパイダー〈primitive spider〉と呼びます。

汎用のスパイダー

ノード・ワイヤー図を描くとき、たいてい（常にとは言ってない）使ってよい汎用の基本スパイダーがあります。

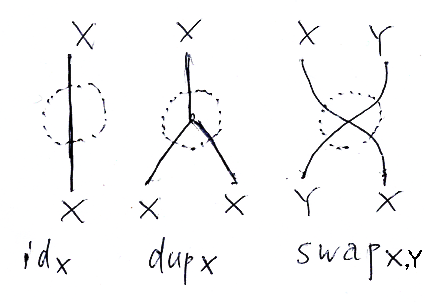
左から、

Xの恒等〈identity〉
Xの複製〈duplication〉
XとYの入れ替え〈swap〉

これらもりっぱなスパイダーですが、ノードのアイコンは描かずに、ワイヤー／ワイヤーの分岐／ワイヤーの交差として描きます。

ここで使っている文字'X', 'Y'は、具体的なワイヤーラベルではなくて、勝手なラベルに置き換えてよいパラメータです。具体的なラベルではないパラメータを持つスパイダー〈ノード・ワイヤー図〉は総称スパイダー〈総称ノード・ワイヤー図〉と呼びます。ちなみに、「汎用」も「総称」も"generic"の訳語です。

※注意： id, dup, swap以外に、discと書かれる「入力を捨ててしまう操作」もよく使われる汎用スパイダーです。id, dup, swap, discは、象形文字で、I, X, 人, ! とも書かれます。象形文字については、「整数式の構文解析木 (A4P3) // IXY記法」、「単純式の操作の操作 (A5P4) // 例題」にも象形文字が登場します。

今述べた id, dup, swap のように、最初から使ってよいと約束した総称パイダーを基本総称スパイダー〈primitive generic spider〉と呼びます。

念の為、言葉の注意をしておくと：

「汎用」と「総称」はどちらも"generic"の訳語で同義。
「基本」の代わりに、「原始」、「原子」、「組み込み」なども使う。

いちいちは注意しないでしょうが、ほとんど常に、山のような同義語・類義語があります。

スパイダーの構成問題

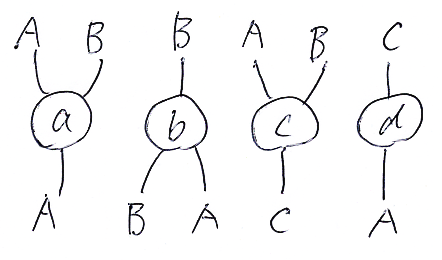
次のようなスパイダーのセット {a, b, c, d} があるとします。

これらのスパイダーを分解する気はないので、a, b, c, d は基本スパイダーと考えます。
問題： これら基本スパイダーと基本総称スパイダー（前節）を素材として、結合（演算子記号は';'）と併置（演算子記号は' $\otimes$ '）により、次のプロファイルを持つスパイダー〈ノード・ワイヤー図〉を構成してください。ただし、構成できる保証はありません。解答の形式はすぐ下の例題を見てください。

B, A → A
B, A → B
B, A → C
A → A, B
B → A, B
C → A, B
C, C, B → A, A
B, B → A, A

例題： A, B, B → A, A, B というプロファイルを持つスパイダーを構成せよ。

要求されているプロファイルを持つスパイダーを横棒記法の図で書けば：

   A  B       B
  ------ a ------ b
    A       B  A
  ---- id  ------ swap
    A       A  B

このスパイダーが構成される過程を書けば：

    ☆        ☆             ☆          ☆
  ====== Ent ===== Ent      ===== Ent  ====== Ent
   A  B        B              A         B  A
  ------ a   ----- b         --- id    ------ swap
    A         A  B            A         A  B
  =========+========= Prod  =========+========= Prod
     A  B      B                A      B  A
    ------ a ----- b           --- id ------ swap
       A      B  A              A      A  B
   ======================+======================= Comp
                  A  B       B
                 ------ a ------ b
                   A       B  A
                 ---- id  ------ swap
                   A       A  B

ここで、

Ent ： Enter -- 基本スパイダー（総称スパイダーの具体化も含む）を登場（入場）させる。
Prod ： Product -- スパイダーの併置（直積ともいう）を作る。
Comp ： Composition -- スパイダーを結合する。

併置〈直積〉を表す演算子記号' $\otimes$ 'を使ったほうが分かりやすいかも知れません。



    ☆        ☆             ☆          ☆

  ====== Ent ===== Ent      ===== Ent  ====== Ent

   A  B        B              A         B  A

  ------ a   ----- b         --- id    ------ swap

    A         A  B            A         A  B

  =========+========= Prod  =========+========= Prod

       A  B   B                  A   B  A

      ------------ ab         ---------- idswap

       A   B  A                  A   A  B

   ======================+======================= Comp

                      A  B  B

                     --------- ab

                      A  B  A

                     --------- idswap

                      A  A  B

出来たスパイダー（上の図の最下段）をテキストの式で書けば：

(a $\otimes$ b);(id $\otimes$ swap)

なお、横棒記法よりは入れ子のノード・ワイヤー図のほうが望ましいです。描くのがめんどくさいけど、圧倒的に望ましいです。是非に描いてみてください。入れ子のノード・ワイヤー図の例は、次のアンカー〈リンク〉をクリックしてください。

入れ子のノード・ワイヤー図

描き方の説明は：

絵図の描き方と省略法 (A16)

最も基本的なことは：

ノード・ワイヤー図〈ストリング図〉 (A1)

結局、この節冒頭の問題の解答は、次の3つの形式をすべて書いて（描いて）ください。

（もしあれば）目的のスパイダーのノード・ワイヤー図
目的のスパイダーを作る過程を描いた入れ子のノード・ワイヤー図
目的のスパイダーのテキスト表現

問題： 構成できるものに関しては、もうひとつ別なスパイダー（別ならなんでもいいです）も作ってください。

構成可能性／構成不可能性定理

プロファイルを勝手に指定されたときに、そのプロファイルを持つスパイダーが構成できるとは限りません。構成できないときもあります。しかし、「頑張ったけれども構成できなかった」では、構成不可能性は言えません。「これこれのタイプのプロファイルに対しては、スパイダーを構成できない」という定理を示せば構成不可能性が言えます。

一方、「これこれのタイプのプロファイルに対しては、スパイダーを必ず構成できる」という定理があれば、実際に構成しなくても構成可能性が言えます。

前節の設定で、次の定理が成立します。

構成不可能性定理：プロファイルの形が Γ → B であるプロファイルに対して、スパイダーは構成できない。ただし、Γは、A, B, C からなるリストで、B（単一のB）ではない。（[追記]←Γに関する条件が抜けていたので追記した。[/追記]）
構成不可能性定理：プロファイルの形が Γ → Δ で、リストΓ内にBが出現せず、リストΔ内にBが出現するとき、このプロファイルに対してスパイダーは構成できない。（[追記]この定理は変更しました。「スパイダーの構成不可能性定理を変更 (A18)」を参照。[/追記]）
構成可能性定理：プロファイルの形が B → Δ で、ΔはAとCから構成されるリスト（非空でBは含まないリスト）のとき、このプロファイルに対してスパイダーは構成できる。

問題： これらの定理を証明せよ。

これは、ごく普通の問題で、ごく普通の証明を書けばいいのです。形式化した命題や、形式化した証明ではなくて、今までどおり、いつもどおりの自然言語で書かれた通常の証明を要求しています。

スパイダーパズル

前々節の問題のように、プロファイルを与えて、そのプロファイルを持つスパイダーを構成する問題をスパイダーパズル〈spider puzzle〉と呼びましょう。ちょっとピクチャーパズル（ジグソーパズル）と似てます。

ピクチャーパズルと同様に、使ってよい素材〈ピース〉のストックと、組み合わせ方のルールがあります。前々節のスパイダーパズルのルールは：

id, dup, swap という総称スパイダーを具体化して素材として使ってよい。
a, b, c, d という4つのスパイダーは素材として使ってよい。
併置により組み合わせてよい。
結合により組み合わせてよい。

ルールは、いくらでもカスタマイズできます。決めるべきは：

使ってよい基本スパイダー（総称と総称ではないもの）のセット
使ってよい組み合わせ方のセット

スパイダーパズルの遊び方は、ピクチャーパズルとは違って：

出題者が、プロファイルを指定する。
解答者が、そのプロファイルを持つスパイダーを構成しようと頑張る。

当然に、解答者は最初に決めた素材と組み合わせ方の範囲内で構成を行います。ルールを守らないとダメです。

形式化された証明は、スパイダーパズルと同じ構造を持ちます。素材や組み合わせ方がもっと複雑になるだけです。人間が現実世界で行っている証明という行為を、ルールを持つパズル（ゲーム）として定式化して、それをコンピュータ上で動くソフトウェアシステムとして実現可能なほどに明確にしよう、ということです。必然的に、証明を行ったり助けたりするソフトウェアはゲームソフトに近くなります（「業務ソフトまたはゲームソフトとしてのCoq （誰も書かないCoq入門以前 2）」参照）。

*1:画像： https://www.mitsuiwa.co.jp/product/list/msview/device/ より

*2:画像： https://www.mudpuppy.com/collections/puzzles より