このブログは、旧・はてなダイアリー「檜山正幸のキマイラ飼育記 メモ編」（http://d.hatena.ne.jp/m-hiyama-memo/）のデータを移行・保存したものであり、今後（2019年1月以降）更新の予定はありません。

今後の更新は、新しいブログ http://m-hiyama-memo.hatenablog.com/ で行います。

絵図の描き方と省略法 (A16)

RSS練習問題

※この記事は「記事16」

次の問題はやってみましたか？

解答（の一例）は次の記事にあります。

引き続く次の記事も類似の問題です。

どれも、「絵図を描きましょう」という問題です。練習で描いたような絵図は、人間が目視できるだけでなく、コンピュータにとっても扱いやすいんです。コンピュータのメモリ内に展開するデータとして、ツリー構造やグラフ構造を表現することは容易です。したがって、絵図の操作（変形や組み合わせ）は、データを処理するアルゴリズムとして定式化できます。（興味があれば、「ともかくシーケントなんだから、頼むよ、皆んな (A12) // 形式化とシーケント」も参照。）

この記事では、完全な絵図とその省略（節約）図法について、オハナシとして述べます。オハナシですから、細部が理解できなくても気にすることはありません。今は、証明の形式化への（心の）準備として読んで、後でまた細部まで確認するのがよいでしょう。

内容：

  1. 絵図を完全に描く
  2. テキストによる表現
  3. 省略法

絵図を完全に描く

「ノード・ワイヤー図と横棒記法の例と練習 (A2P1)」の問題に出したノード・ワイヤー図を、ノード・ラベルである等式系も省略せずに描くと次のようでした（「問題集1の目的と解答と追加説明 重要！ (A13R1)」の図を再掲）。

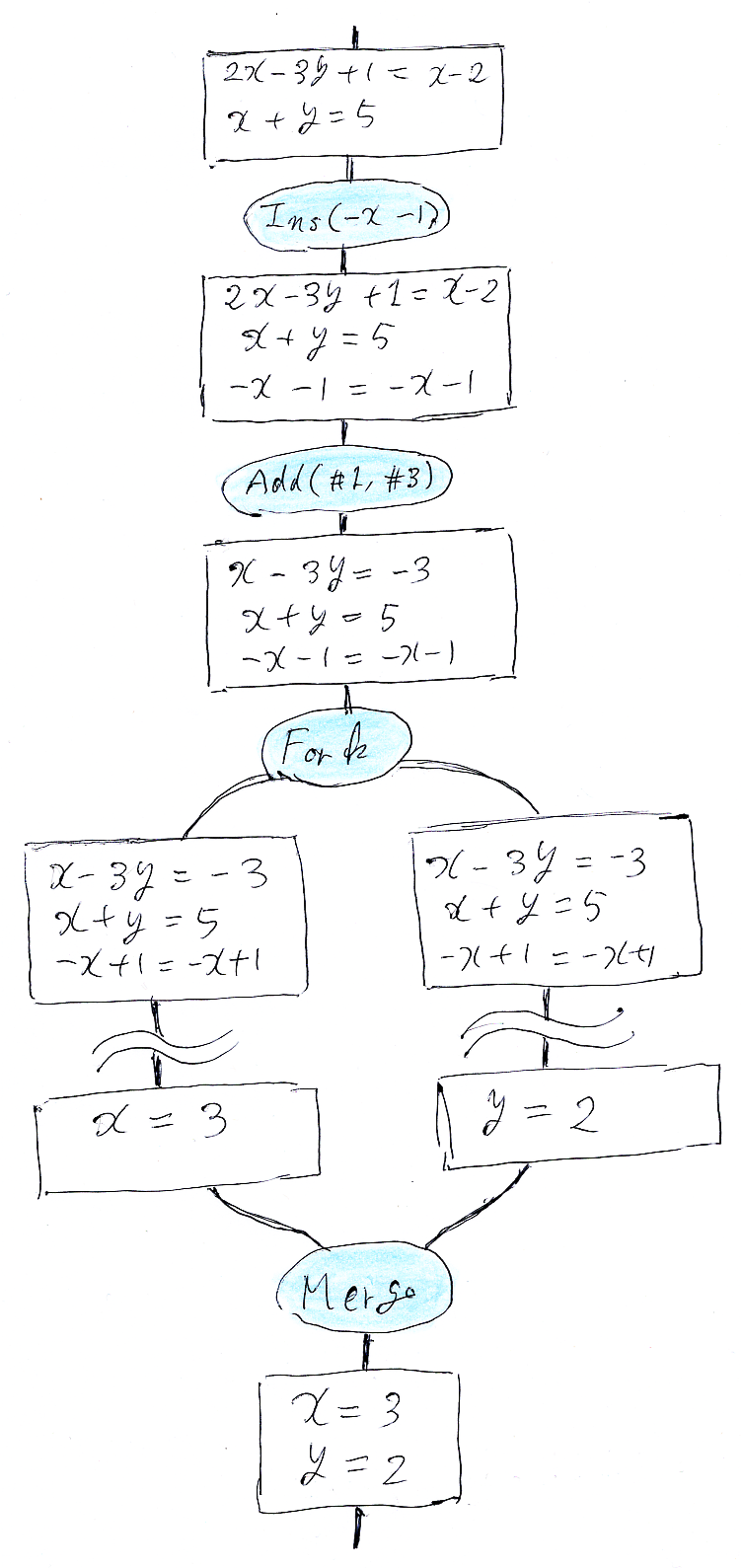
この図をテキスト（文字）でなんとか表現するには横棒記法を使います。

         2x - 3y + 1 = x - 2
         x + y = 5
       ---------------------- Ins(-x - 1)
         2x - 3y + 1 = x - 2
         x + y = 5
         -x - 1 = -x - 1
       -------------------- Add(#1,#3)
         x - 3y = -3
         x +  y =  5
         -x - 1 = -x - 1
  ---------------------------------- Fork
   x - 3y = -3       x - 3y = -3
   x +  y =  5       x +  y =  5
   -x - 1 = -x - 1   -x - 1 = -x - 1
  〜〜〜〜〜〜〜〜   〜〜〜〜〜〜〜〜〜
  〜〜〜〜〜〜〜〜   〜〜〜〜〜〜〜〜〜
    x = 3             y = 2
   -------------------------- Merge
            x = 3
            y = 2

「問題集1の目的と解答と追加説明 重要！ (A13R1)」で出したもうひとつの絵図に関して次のように書きました。

形式化された証明を分かりやすく図示するには、この程度の絵が必要になる。これでも、相当に省略していて、もっと細部を描き込むとさらに複雑になる。

同じ図を、今度は省略なしで描いてみます。

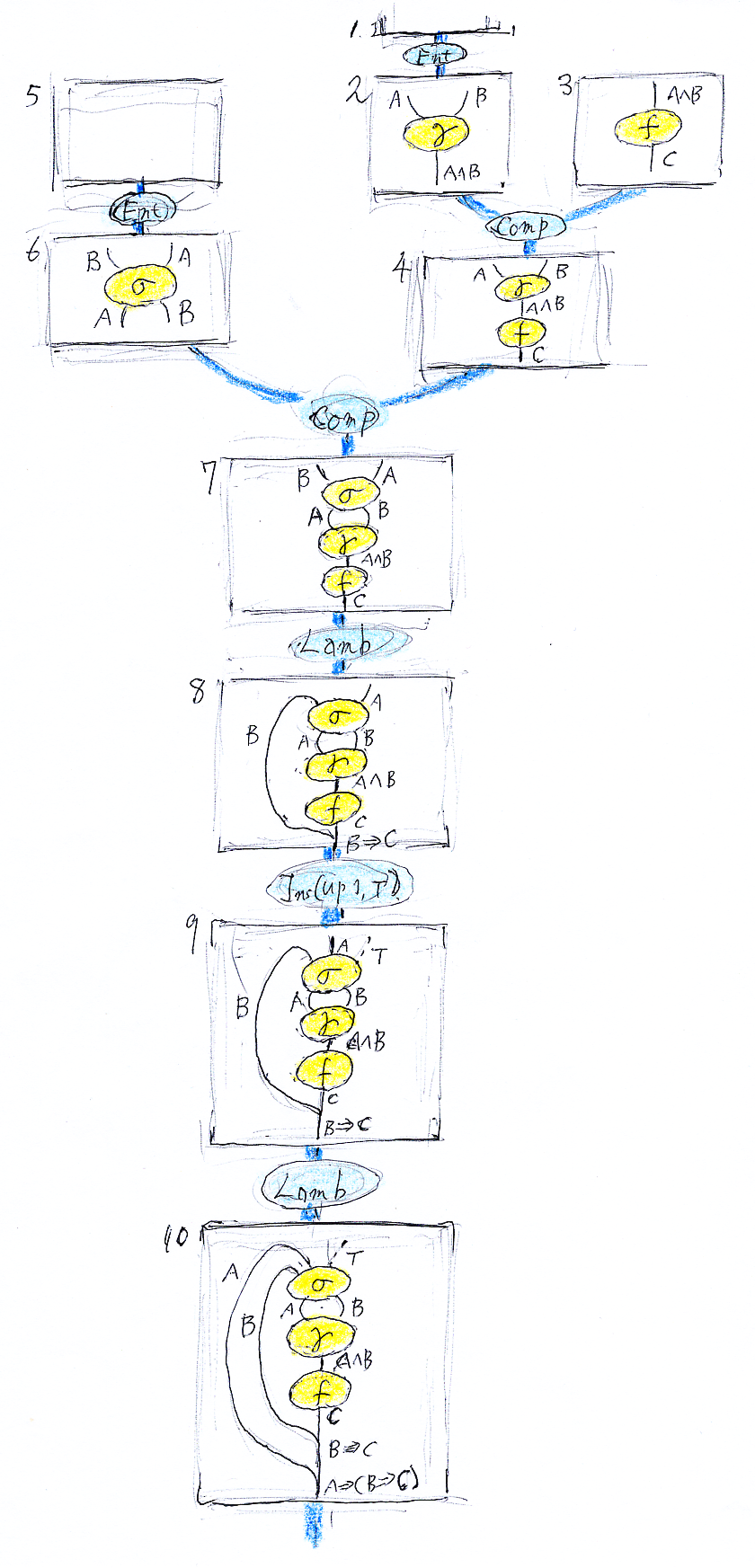
テキストによる表現

前節の図（二番目のほう）は、ワイヤーラベルとしてノード・ワイヤー図が付いているので、結果的に入れ子のノード・ワイヤー図になります。ワイヤーラベルを入れるラベルフレーム（四角い枠）内にノード・ワイヤー図が描いてあります。

8番と番号が付いたフレーム内の絵を見てみます。

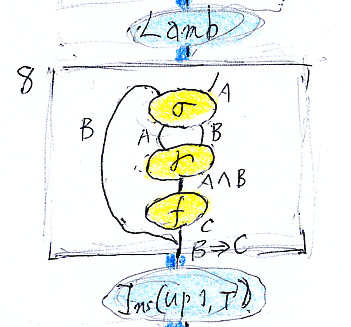
左側にBとラベルされた曲がったワイヤーがあります。この絵を、次のような横棒記法で書いては、曲がったワイヤーの情報が抜けてしまいます。

    B     A
  ---------- σ
    A     B
  ---------- γ
     A∧B
    ------- f
       C
    -------
      B⇒C

曲がったワイヤーをテキストで表現する方法はいくつかありますが（実情は、みんなそれぞれ勝手な表記を使っている）、例えば、次のようにして曲がったワイヤーを表すことができます。

   #1
  -----
    B     A
  ---------- σ
    A     B
  ---------- γ
     A∧B
    ------- f
       C
    ------- ∩(#1)
      B⇒C

上の'#1'は番号付けで、下の'∩(#1)'は、#1から出た曲がったワイヤーがここで合流することを示す目印です。この記法を使って、入れ子のノード・ワイヤー図を横棒記法にしましょう。空白のフレームは'☆'で表します。

                  ☆
               ========= Ent
                  A  B       A∧B
                 ------ γ  ------ f
    ☆            A∧B        C
 ======== Ent   ===================== Comp
  B   A                 A  B
  ------ σ            ------ γ
  A   B                 A∧B
                       ------ f
                          C
 ================================ Comp
            B  A
           ------- σ
            A  B
           ------ γ
            A∧B
           ------ f
              C
 ============================ Lamb
           #1
          ----
           B    A
          -------- σ
           A    B
          -------- γ
            A∧B
           ----- f
             C
           ----- ∩(#1)
            B⇒C
 ============================ Ins(up 1, T)
           #1
          ----
           B    A  T
          ----------- σ
           A    B
          -------- γ
            A∧B
           ----- f
             C
           ----- ∩(#1)
            B⇒C
 ============================ Lamb
           #1    #2
          ----  ---
           B     A   T
          ------------- σ
           A    B
          -------- γ
            A∧B
           ----- f
             C
           ----- ∩(#1)
            B⇒C
         --------- ∩(#2)
         A⇒(B⇒C)

イラストが使えない場合でも、省略無しで完全な入れ子横棒記法の図を使うなら、証明の形式化はかなり簡単です -- 難しくはありません。ただし、とても手間と紙面（紙の面積）を要することにはなります。

※注意： 次の図は実際は不正確で、Tが上に乗れば、もはやσではありません。σ以外のラベルを使ったほうがいいのですが、Tが乗っただけでいちいちラベルを変えるのも面倒だったので、同じσでラベルしています。これも、ことを分かりにくくする略記ではありますが。

    B    A  T
   ----------- σ
    A    B

省略法

手間と紙面を節約するために、絵図を省略して描く方法があります。しかし、省略すれば分かりにくくなります。「手間と紙面」と「分かりやすさ」はトレードオフの関係にあり、大幅な省略をした記法は難解です。

代表的な省略法は二種で：

  1. 「最後の一枚だけ」で済ます方法
  2. 「プロファイルだけ」で済ます方法

「最後の一枚」は、先の例で言えば、次の図だけを提示する方法です。

   #1    #2
  ----  ---
   B     A   T
  ------------- σ
   A    B
  -------- γ
    A∧B
   ----- f
     C
   ----- ∩(#1)
    B⇒C
 --------- ∩(#2)
 A⇒(B⇒C)

簡単な場合は「最後の一枚」だけでも何とかなりますが、過程が複雑になると、最後の一枚だけでそれに至る過程を想像するのは困難です。過程を想像するヒントとして注釈を入れたりしますが、その注釈の入れ方のルールを考えたり覚えたりする手間が増えます（本末転倒な感じ）。

フレーム内のノード・ワイヤー図のプロファイルとは、入力列と出力列の仕様です（入力列／出力列に関しては「整数式の操作 (A3P2)」）。プロファイルは、「入力列 → 出力列」という、シーケントの形になります。

先の例を、「プロファイルだけ」方式で書いてみます。

                            ☆
                      ============== Ent
      ☆               A, B → A∧B      A∧B → C
 ============== Ent   ============================== Comp
  B, A → A, B                A, B → C
 ======================================= Comp
         B, A → C
 ============================ Lamb
            A → B⇒C
 ============================ Ins(up 1, T)
         A, T → B⇒C
 ============================ Lamb
            T → A⇒(B⇒C)

入門段階では「最後の一枚」方式、より進んだ学習では「プロファイルだけ」方式が使われる傾向があります。どちらがいいか？という議論はあまり意味がありません。どちらも良くないので。

完全な絵図を実際に描いてみること、省略されても完全な絵図をイメージできるように今後トレーニングすることが重要です。

「手間と紙面 vs. 分かりやすさ」というトレードオフでは、ほとんど常に「分かりやすさ」を犠牲にして「手間と紙面」を節約する選択肢が採用されます。コストという深刻な要因があるので致し方ないのですが、論理の啓蒙と普及にとっては、大変に悲劇的な事態です。

事態が変わるには、30年、50年という時間がかかるでしょう。興味があれば、次の本編記事をどうぞ。

問題集8の解答と解説： 当たり前であることを証明する (A15R8-1)

RSS練習問題

※この記事は「記事15 解答8-1」

問題集8とは、次の記事（の問題部分）のことです：

「シーケントとスコット・ブラケット (A10P8) // 組み込み推論を表すシーケント」の解答例＋解説。


シーケント (x, y∈R), x2 = -3, x ≧ 0 → 1 + 1 = 3 を、日本語風に読み下してみます。



実数 x, y に対して、

x2 = -3, x ≧ 0 だとする。

これらから、

  1 + 1 = 3

が出る。

「何を言ってるんだ？ これは」と思うかも知れませんが、このシーケントの“正しさの度合い”はスコット・ブラケットを計算すれば分かります。日本語で考えるのは現実世界での話で、形式化された世界（モデルの世界、演繹システムの世界）での形式化された主張（＝シーケント）の正しさは、スコット・ブラケットと呼ばれる関数の関数値で測るのでした。



   〚(x, y∈R), x2 = -3, x ≧ 0 → 1 + 1 = 3〛

 = 〚x, y∈R| x2 = -3, x ≧ 0〛c ∪ 〚x, y∈R| 1 + 1 = 3〛
左辺のスコット・ブラケットと右辺のスコット・ブラケットを別々に計算する：
   〚x, y∈R| x2 = -3, x ≧ 0〛

 = 〚x, y∈R| x2 = -3〛∩〚x, y∈R| x ≧ 0〛

 = 0∩{(x, y)∈R2| x ≧ 0}

 = 0
   〚x, y∈R| 1 + 1 = 3〛

 = 0
もとの計算に戻って：
 = 〚x, y∈R| x2 = -3, x ≧ 0〛c ∪ 〚x, y∈R| 1 + 1 = 3〛

 = 0c ∪ 0

 = R2∪ 0

 = R2

このシーケントのコンテキストは、(x, y∈R) = (x∈R, y∈R) で、コンテキスト領域はR2、したがって、

  • 〚(x, y∈R), x2 = -3, x ≧ 0 → 1 + 1 = 3〛 = Dom((x∈R, y∈R)) = R2

スコット・ブラケットの値がコンテキスト領域と一致するシーケントは正しい（そう定義している）から、

  • シーケント (x, y∈R), x2 = -3, x ≧ 0 → 1 + 1 = 3 は正しい。

ここで出てきた「正しい」は完全にテクニカルタームであり、既に定義済みです。「関数が連続である」とか「ベクトル空間は有限次元である」とかと同様に「シーケントは正しい」はテクニカルな主張です。

解析学で「この関数は連続なんじゃないの？ 5,6個の点つないだグラフを見ると、そんな感じ」「いやぁ、どことなく不連続な雰囲気があるなぁ」とかの議論がナンセンスであると同様に、「このシーケントは正しいんじゃないの？ 日本語にしてみると、そんな感じ」とか「いやぁ、どことなく正しくない雰囲気があるなぁ」とかの議論はナンセンスです。定義があるんだから、定義にしたがって「正しい」（あるいは「正しくない」）を示す、それしかありません。

次に、シーケント (), 1 + 1 = 2 → 1 + 1 = 2 を考えましょう。ここで、() は空なコンテキストであり、その領域は Dom(()) = 1 です。

日本語風読み下しは：



1 + 1 = 2 だとする。

これにより、

  1 + 1 = 2

が出る。

スコット・ブラケットを計算してみると：



   〚(), 1 + 1 = 2 → 1 + 1 = 2〛

 = 〚| 1 + 1 = 2〛c ∪ 〚| 1 + 1 = 2〛

 = 1c ∪ 1

 = 0 ∪ 1

 = 1

したがって、

  • シーケント (), 1 + 1 = 2 → 1 + 1 = 2 は正しい。

シーケント (), 1 + 1 = 3 → 1 + 1 = 3 はどうでしょう？ 四の五の言わずにスコット・ブラケットを計算：



   〚(), 1 + 1 = 3 → 1 + 1 = 3〛

 = 〚| 1 + 1 = 3〛c ∪ 〚| 1 + 1 = 3〛

 = 0c ∪ 0

 = 1 ∪ 0

 = 1

より一般に、αをコンテキスト、Aを論理式として、α, A → A という形をしたシーケントはすべて正しいと思われますよね。



α に対して、

A だとする。

これにより、

  A

が出る。

これは当たり前に聞こえます。もちろん、日本語読み下しなんて当てにはならないですけど。当てになるのは、スコット・ブラケットの定義にしたがった証明（通常の証明、現実世界の数学的行為としての証明）です。やってみます。


Dom(α) = X とすると、〚α| A → A〛 は Pow(X) に値を取る。

  • 〚α| A → A〛 = 〚α|A〛c ∪ 〚α|A〛

どんな部分集合 S ⊆ Pow(X) に対しても、

  • Sc ∪ S = X

は成立するから、

  • 〚α| A → A〛 = 〚α|A〛c ∪ 〚α|A〛 = X

したがって、

  • 〚α| A → A〛 = Dom(α)

よって、シーケント α A → A は、コンテキストα、論理式Aによらずに常に正しい。

α, A → A だけでなく、α, A → T や α, A∧B → A もいかにも当たり前です。しかし、「日本語読み下しにしてみたら、当たり前に聞こえたから」なんてのは何の根拠にもなりません。そんなことではくて、通常の数学の証明として当たり前さを確認しましょう。「通常の」ですから形式化する必要はありません。自然言語で普通に証明を書けばいいのです。形式化された証明（近々定義する）は、我々人間同士のコミュニケーションに使うものではなくて、演繹システムの内部データ／内部処理のことです。

我々が、人工的な構築物である演繹システムの内部で遂行される形式化された証明を調べようとしているのは確かです。だからといって、現実世界での通常の数学的行為を捨てたり変えたりする必要はまったくありません。いつもどおり、今までどおり、普通の／通常の証明（＝メタ証明）をすればいいのです。

何度も同じことを繰り返しますが：

  1. 論理の数学的モデルは人工的なシステムであり、天然に存在しないし、神様やサンタさんがプレゼントしてもくれない。
  2. したがって、論理の数学的モデルは、人間がゼロから細部に渡って構築（定義）しなくてはならない。“数学的”モデルなのだから、構築の方法は完全に数学的であり、雰囲気的な曖昧な議論は許されない。
  3. 以上のことを我々生きている人間が現実世界で行うにあたり、今までの考え方／やり方を変える必要はない。現実世界で使っている素朴集合論と、現実世界で使っている古典論理は今まで同様に普通に使う。

問題集6の目的と解答と追加説明 その2 (A14R6-2)

RSS練習問題

※この記事は「記事14 解答6-2」

問題集6とは、次の記事（の問題部分）のことです：

「その1」は、次の記事です。

内容：

  1. 書き方の注意
  2. 限量子を含む閉論理
  3. コンテキスト付き論理式
  4. コンテキスト付き論理式（続き）
  5. コンテキストの水増し
  6. 様々な論理式を作ってみる
  7. 限量子も使ってみる

書き方の注意

次の書き方の約束は、あまり（ほとんどかも）使っていません。

  • メタ論理（形式されてない通常の論理）の論理記号は丸括弧で囲む。(∧), (⇒) など。
  • 形式化された命題である論理式は引用符で囲む。"∀x∈R.∃y∈R.(y2 = x)" のように。

形式化されている／されてないを特に強調したいときは、気まぐれに使います。

限量子を含む閉論理

前回は、「限量子を含む閉論理」の途中まででした。解答を再掲すると：

  1. 〚∀n∈N.(n ≧ 0)〛 = 1
  2. 〚∃n∈N.(n < 0)〛 = 0
  3. 〚∀n∈N.∃m∈N.(m ≧ n)〛 = 1
  4. 〚∀n∈N.∃m∈N.(m < n)〛 = 0
  5. 〚∀x∈R.∃y∈R.(y2 = x)〛 = 0
  6. 〚∀x∈R.∃y∈R.(x ≧ 0 ⇒ y2 = x)〛 = 1
  7. 〚∃y∈R.∀x∈R.(x ≧ 0 ⇒ y2 = x)〛 = 0
  8. 〚∀x∈R.∀y∈R.∃n∈N.((x ≧ 0 ∧ y > 0) ⇒ yn ≧ x)〛 = 1

3番以降は、限量子が2つ付いています。「命題と、そのコンテキスト／真理集合 (A8P6)」の追記に書いた「感情表現をタップリ混じえた日本語」に沿って考えれば、おそらく解答は得られるでしょう。

しかし、2個以上の限量子が付いた形式化された論理式の数学的解釈は、日本語としての解釈とは別に定義する必要があります。なぜなら、形式化された論理式は人工的に定めた構文的なデータに過ぎず、我々人間が意味を定義してあげないと、天然の意味などないからです。

「意味を定義してあげる」作業は、国語辞典の項目を書き下す作業ではありません。「問題集6の目的と解答と追加説明 (A14R6-1)」において、1個の限量子に対してやったのと同程度の精度の議論が必要です。が、これはちょっとめんどうなので、オプショナルな（必須ではない）別記事にします（短い解説なら、この記事の最後にあります）。

コンテキスト付き論理式

  1. (x∈R| x < 0 ∨ 1 < x)
  2. (x∈R| 0 < x ∧ x < 1)
  3. (x∈R| 0 < x ∧ 1 < x)
  4. (x∈R| x < 0 ⇒ x2 = 1)
  5. (x∈R| x2 = 1 ⇒ x < 0)
  6. (x∈R| x2 = 1 ⇒ x = 0)
  7. (x∈R| x2 = 1 ⇒ x = 1)
  8. (x∈R| x2 = 1 ⇒ (x = 1 ∨ x = -1))
  9. (x∈R| (x2 = 1 ∧ x ≧ 0) ⇒ x = 1)
  10. (x∈R| (x2 = 1 ∧ x ≧ 0) ⇒ (x = 1 ∨ x = -1))
  11. (x, y∈R| x2 + y2 = 1)
  12. (x, y∈R| x2 + y2 = 4 ∧ x + y ≧0)
  13. (x, y∈R| x2 + y2 = 4 ∧ x + y ≧ -1)
  14. (x, y∈R| x2 + y2 = 1 ∨ x + y = 0)
  15. (x, y∈R| x2 + y2 = 1 ⇒ x = 1)
  16. (x, y∈R| x = 1 ⇒ x2 + y2 = 1)
  17. (x, y∈R| (x = 1 ∧ y = 0) ⇒ x2 + y2 = 1)
  18. (x, y∈R| x2 + y2 = 1 ⇒ x + y ≦ 2)
  19. (x, y∈R| x2 + y2 = 1 ⇒ x + y ≦ 1)
  20. (x, y∈R| x2 + y2 ≦ 1 ⇒ x + y ≦ 2)
  21. (x, y∈R| x2 + y2 ≦ 1 ⇒ x + y ≦ 1)
  22. (x, y∈R| (x2 + y2 ≦ 1 ∧ x + y ≦ 0) ⇒ x + y ≦ 1)

1から10のスコット・ブラケットを図示すると次のようです。コンテキスト領域は、R = 直線 で、赤い所がスコット・ブラケットの値（真理集合）です。赤くない所は真理集合の補集合、つまり反例集合です。

実数の区間を、閉区間 [a, b] 、開区間 (a, b) のように書くと：

  1. 〚x∈R| x < 0 ∨ 1 < x〛 = (-∞, 0)∪(1, +∞)
  2. 〚x∈R| 0 < x ∧ x < 1〛 = (0, 1)
  3. 〚x∈R| 0 < x ∧ 1 < x〛 = (1, +∞)
  4. 〚x∈R| x < 0 ⇒ x2 = 1〛 = {-1}∪[0, +∞)
  5. 〚x∈R| x2 = 1 ⇒ x < 0〛 = (-∞, 1)∪(1, +∞)
  6. 〚x∈R| x2 = 1 ⇒ x = 0〛 = (-∞, -1)∪(-1, 1)∪(1, +∞)
  7. 〚x∈R| x2 = 1 ⇒ x = 1〛 = (-∞, -1)∪(-1, +∞)
  8. 〚x∈R| x2 = 1 ⇒ (x = 1 ∨ x = -1)〛 = (-∞, +∞)
  9. 〚x∈R| (x2 = 1 ∧ x ≧ 0) ⇒ x = 1〛 = (-∞, +∞)
  10. 〚x∈R| (x2 = 1 ∧ x ≧ 0) ⇒ (x = 1 ∨ x = -1)〛 = (-∞, +∞)

含意'⇒'を含む (x∈X| A⇒B) の形のコンテキスト付き論理式のスコット・ブラケットを求めるときは、いちいち悩まないで定義どおりに計算します。

  • 〚x∈X| A⇒B〛 = 〚x∈X| A〛c∪〚x∈X| B〛

例えば、"(n∈N| nは偶数 ⇒ n2は偶数)" のスコット・ブラケットならば：



    〚n∈N| nは偶数 ⇒ n2は偶数〛

  = 〚n∈N| nは偶数〛c∪〚n∈N| n2は偶数〛

  = {n∈N| nは奇数}∪{n∈N| n2は偶数}

ここで、{n∈N| nは奇数}が真理集合に入ってますが、これを真理集合に入れないと、奇数の集合は真理集合の補集合、つまり反例の集合になってしまいます。奇数が反例なのではなくて、

  • 偶数であって、その二乗は偶数ではない自然数

が反例です。

反例ではない自然数は正例、つまり真理集合＝スコット・ブラケットに入ります。コンテキスト領域（今の場合はN）の要素は、必ず正例か反例のどちらかです。「正例でも反例でもない」とか「正例でもあり反例でもある」なんて要素は在りません！ 「Yesとも言えるしNoとも言える」なんて答え方は、まったく許されないのです。

※注意： 「nは偶数」は日本語ですが、"∃k∈N.(n = 2k)" とすれば形式化された命題になります。全部を形式化した形にすると長くなるので、一部を非形式的に日本語で書く略記はしばしば使います。定式化や理論構成自体は厳密でも、説明や表現はとても雑でエエカゲンなんです。

コンテキスト付き論理式（続き）

問題11から15の図は次のようになります。13は間違っていたので、後から描きなおしています。コンテキスト領域は、R×R = R2 = 平面 で、赤い所がスコット・ブラケットの値（真理集合）です。赤くない所は真理集合の補集合、つまり反例集合です。


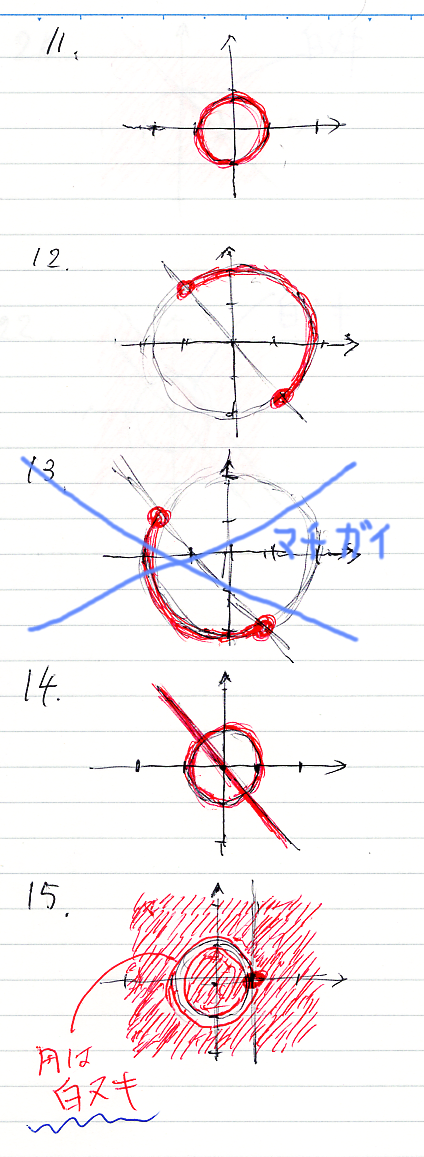
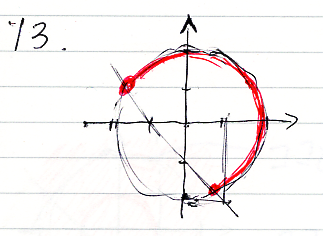
15は汚いですが、円周が白ヌキ（補集合、反例）です。が、点 (1, 0)は赤（正例）です。

続いて、16から22まで。


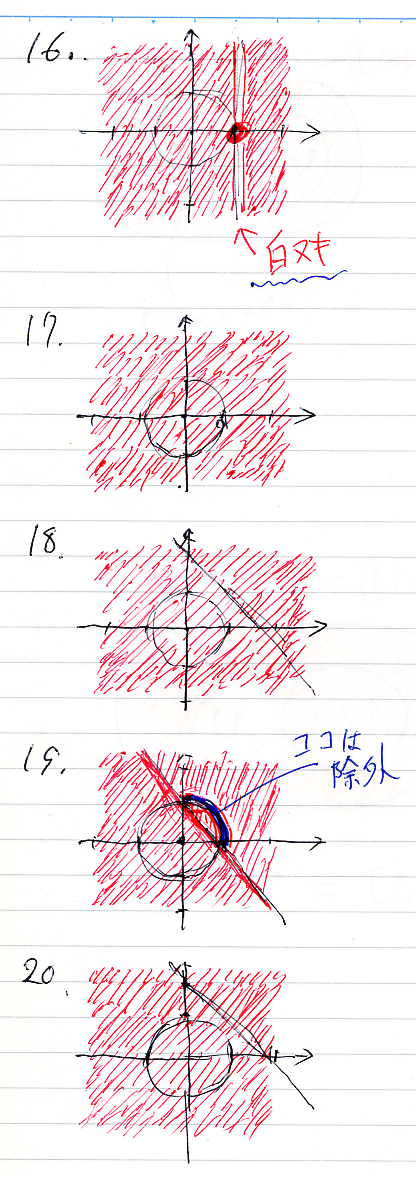
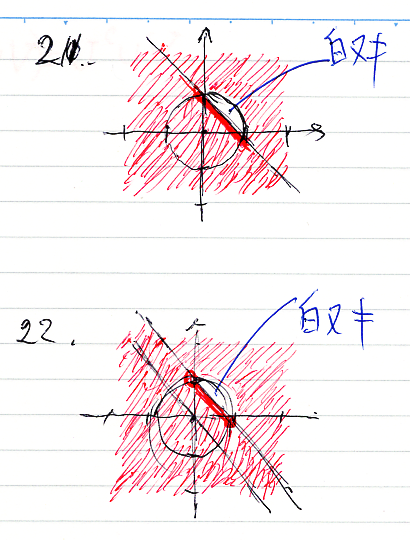
19は青で塗っちゃいましたが、白ヌキ（補集合、反例）のつもりです。

コンテキストの水増し

  1. (x, y∈R| x < 0 ∨ 1 < x)
  2. (x, y∈R| 0 < x ∧ x < 1)
  3. (x, y∈R| 0 < x ∧ 1 < x)
  4. (x, y∈R| x < 0 ⇒ x2 = 1)
  5. (x, y∈R| x2 = 1 ⇒ x < 0)
  6. (x, y∈R| x2 = 1 ⇒ x = 0)
  7. (x, y∈R| x2 = 1 ⇒ x = 1)
  8. (x, y∈R| x2 = 1 ⇒ (x = 1 ∨ x = -1))
  9. (x, y∈R| (x2 = 1 ∧ x ≧ 0) ⇒ x = 1)
  10. (x, y∈R| (x2 = 1 ∧ x ≧ 0) ⇒ (x = 1 ∨ x = -1))

もとのスコット・ブラケット（真理集合）は、直線内の区間（の寄せ集め）なので、それを上下方向に無限に伸ばした平面領域を描きます。例えば2番なら、幅1で縦方向に無限に長い帯です。

  1. (x, y∈R| 1 + 2 = 3)
  2. (x, y∈R| 1 + 2 < 3)
  3. (x, y∈R| 12 = 22)
  4. (x, y∈R| 3 ≦ 5 ∧ 3 ≦ 3)
  5. (x, y∈R| 1 + 2 < 3 ⇒ 12 = 22)
  6. (x, y∈R| 1 + 2 < 3 ∨ 12 = 22 ∨ 3 ≦ 3)
  7. (x, y∈R| (3 ≦ 5 ∧ 3 ≦ 3) ⇒ 1 + 2 < 3)
  8. (x, y∈R| (3 ≦ 5 ∨ 3 ≦ 3) ⇒ ¬(1 + 2 < 3))
  9. (x, y∈R| ¬(1 + 2 < 3) ⇒ (1 + 2 = 2))
  10. (x, y∈R| 1 + 2 = 3 ⇒ (1 + 2 < 3 ⇒ 12 = 22))
  11. (x, y∈R| ∀n∈N.(n ≧ 0))
  12. (x, y∈R| ∃n∈N.(n < 0))
  13. (x, y∈R| ∀n∈N.∃m∈N.(m ≧ n))
  14. (x, y∈R| ∀n∈N.∃m∈N.(m < n))
  15. (x, y∈R| ∀x∈R.∃y∈R.(y2 = x))
  16. (x, y∈R| ∀x∈R.∃y∈R.(x ≧ 0 ⇒ y2 = x))
  17. (x, y∈R| ∃y∈R.∀x∈R.(x ≧ 0 ⇒ y2 = x))
  18. (x, y∈R| ∀x∈R.∀y∈R.∃n∈N.((x ≧ 0 ∧ y > 0) ⇒ yn ≧ x))

もとの（水増しする前の）コンテキスト領域は1で、スコット・ブラケット（真理集合）が0か1だったので：

  1. もとのスコット・ブラケットが1ならば、平面全体
  2. もとのスコット・ブラケットが0ならば、空集合

様々な論理式を作ってみる

まず、命題パラメータ A, B, C に代入する具体的な論理式を選びます。

  • A として20番を選ぶ： (x, y∈R| 0 < x ∧ x < 1)
  • B として31番を選ぶ： (x, y∈R| x2 + y2 = 4 ∧ x + y ≧ -1)
  • C として29番を選ぶ： (x, y∈R| x2 + y2 = 1)

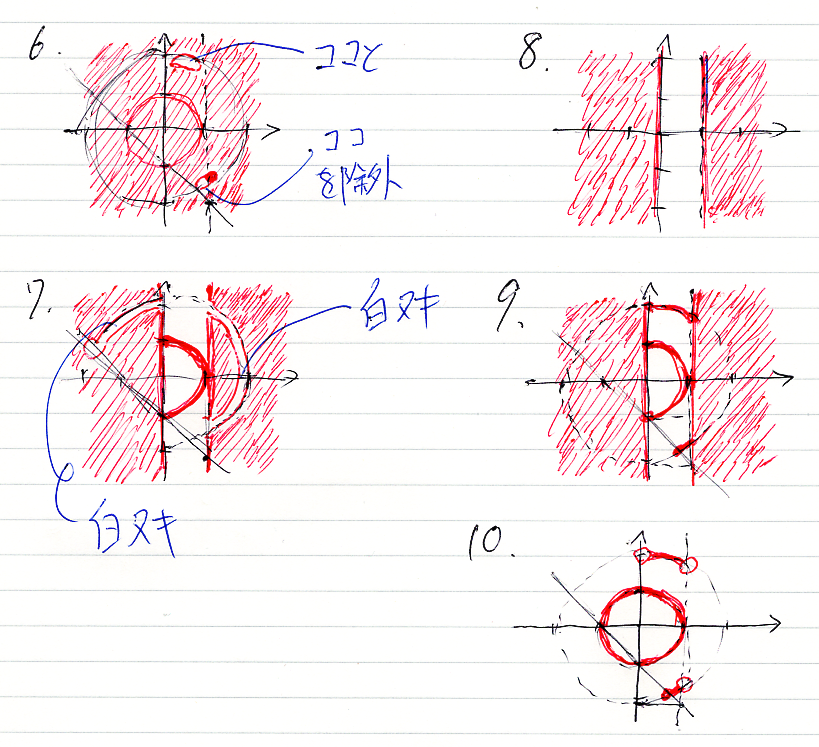
この設定で次の論理式のスコット・ブラケット（真理集合）を描きます。赤い所がスコット・ブラケットの値（真理集合）です。赤くない所は真理集合の補集合、つまり反例集合です。

  1. ¬A
  2. A∧B
  3. A∨B
  4. A⇒B
  5. A⇒¬B
  6. (A∧B)⇒C
  7. (A∨B)⇒C
  8. A⇒B∧C
  9. A⇒B∨C
  10. (A∧B)∨C

こんな(↓)感じ。描く順番がアッチャコッチャ。


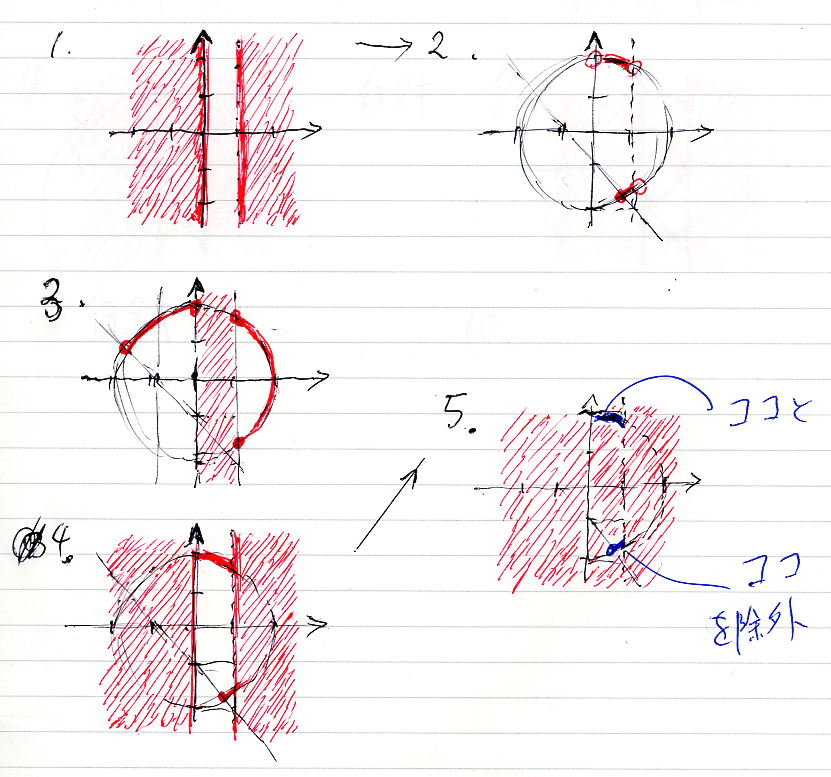
限量子も使ってみる

Aに何を選んでもあまり面白い絵にならないので絵は割愛。

  1. ∀x.A
  2. ∀y.A
  3. ∀x.∀y.A
  4. ∃x.A
  5. ∃y.A
  6. ∃x.∃y.A
  7. ∀x.∃y.A
  8. ∀y.∃x.A

一般に、限量子が付いた場合のスコット・ブラケットの描き方を説明しておきます。

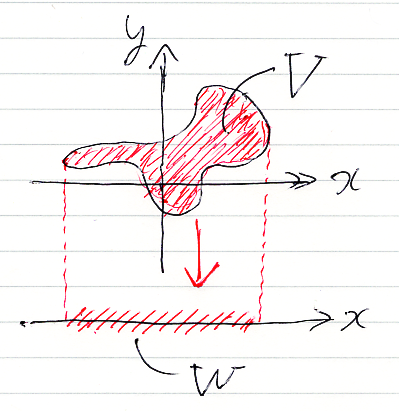
〚x∈R, y∈R| A〛は、コンテキスト領域R2内の部分集合（平面内の図形）なので、それをVと置きます。存在命題のスコット・ブラケット〚x∈R| ∃y∈R.A〛は、集合Vを射影した像です。上の図で射映像はWとなっています。

  • W = (Vの射影像) = 〚x∈R| ∃y∈R.A〛

全称命題 ∀y∈R.A に関しては、

  • ∀y∈R.A と ¬∃y∈R.¬A は論理的に同値

という結果を使って、

  • (Vcの射映像)c = 〚x∈R| ∀y∈R.A〛

これらは、∃y∈R.A と ∀y∈R.A のスコット・ブラケットを計算するときの公式（定義）と思ってもかまいません。つまり、(x∈R, y∈R| A) のスコット・ブラケットが分かれば、それから、∃y∈R.A と ∀y∈R.A のスコット・ブラケットは素朴集合論内で定義・計算が出来るわけです。

問題集6の目的と解答と追加説明 (A14R6-1)

RSS練習問題

※この記事は「記事14 解答6-1」

問題集6とは、次の記事（の問題部分）のことです：

解答だけでなく、「どうしてこのような練習をするか？」や、関連する事項の説明もします。誤解されがちなメタ論理やメタ論理記号、反例と正例の話題にも触れます。

解説も付けたらだいぶ長くなったので、今回は問題集6の途中までです。残りは引き続く記事にします。

内容：

  1. 自然言語へ翻訳しても数学的な意味はない
  2. 限量子を含まない閉論理式
  3. 限量子を含む閉論理式
  4. 反例と正例
  5. 限量子の数学的（素朴集合論的）解釈
  6. 補集合の性質、ついでに「メタ」について
  7. 限量子を含む閉論理式の解説 (途中)

自然言語へ翻訳しても数学的な意味はない

論理記号は次の表と共に導入されます。

記号 意味
∧ かつ
∨ または
¬ ではない
⇒ ならば

この表の右欄の「意味」は、自然言語（日本語）としての意味です。記号 ←→ 日本語 の翻訳が出来ても、数学的な意味は何も確定しません。

記号'∧'の数学的意味を定義するひとつの方法は、∧を {0, 1}×{0, 1}→{0, 1} という写像〈関数 | 演算〉だと解釈して、写像∧の定義を下のように与えることです。ここで、0は偽、1は真を表すとします。

∧ 0 1
0 0 0
1 0 1

他の論理記号も同様にして、写像として数学的意味を確定できます。

しかし、変数xがある場合、

  • 0 ≦ x ∧ x ≦ 1

における'∧'の意味は明らかではありません。次のような解釈があります。

  • xの値が決まれば、0 ≦ x ∧ x ≦ 1 の意味は0（偽）または1（真）として決まる。

しかし、xの値が何であるか不明で、やっぱりよく分かりません。そこでコンテキストを明示して、

  • x∈R| 0 ≦ x ∧ x ≦ 1

これなら、

  • xの値が1/2と決まれば、0 ≦ 1/2 ∧ 1/2 ≦ 1 の意味は1として決まる。
  • xの値が3と決まれば、0 ≦ 3 ∧ 3 ≦ 1 の意味は0として決まる。
  • xの値が0と決まれば、0 ≦ 0 ∧ 0 ≦ 1 の意味は1として決まる。
  • xの値が-1と決まれば、0 ≦ -1 ∧ -1 ≦ 1 の意味は0として決まる。
  • …

結果として、上記のコンテキスト付き論理式は、R→{0, 1} という写像〈関数〉を定義します。より一般には、集合Xから{0, 1}への写像 X→{0, 1} が決まります。

X→{0, 1} という写像達に対して、∧、∨、¬、⇒ という演算を定義しても、もちろんいいのですが、我々にとってより馴染みがあるのは集合演算なので、∧、∨、¬、⇒ （の数学的意味）を集合演算として定義します。写像でも集合でもどっちでもよい理由は：

  • X→{0, 1} という写像 と Xの部分集合のあいだには1：1の対応がある。
  • （すぐ上と同じことだが）写像の集合 Map(X, {0, 1}) と Xのベキ集合 Pow(X) は集合として同型であり、標準的な同型写像がある。
  • 標準的な同型写像は、f |→ {x∈X| f(x) = 1} という対応と、S |→ λx∈X.(if(x∈S) then 1 else 0 end) という対応（互いに逆）で与えられる。

※ λx∈X.(…) は、「… という式で定義される関数」の意味です。

そんな事情で、(x∈R| 0 ≦ x ∧ x ≦ 1) というコンテキスト付き論理式は、Rのベキ集合 Pow(R) の要素（＝Rの部分集合）により意味付けられ、論理記号 ∧、∨、¬、⇒ も、Pow(R)において定義された集合演算（∪, ∩ など）として解釈されます。コンテキスト（の領域）が別な集合Xなら、Pow(X)の集合演算を使います。

以上の内容をまとめると：

  • 〚x∈X| A〛 = {x∈X| A}
  • 〚x∈X| A∧B〛 = 〚x∈X| A〛∩〚x∈X| B〛
  • 〚x∈X| A∨B〛 = 〚x∈X| A〛∪〚x∈X| B〛
  • 〚x∈X| ¬A〛 = 〚x∈X| A〛c （右肩のcは補集合をとることを表す）
  • 〚x∈X| A⇒B〛 = 〚x∈X| A〛c ∪〚x∈X| B〛

これでやっと、論理記号 ∧、∨、¬、⇒ を数学的に議論できる準備ができました。

「記号'∧'は『かつ』の意味です」という説明は、もちろん必要だし、最初はこう言って導入すべきです。が、記号'∧'の数学的意味については何ひとつ規定してないので、論理の数学的モデルの構築には、これっぽっちも役に立ちません -- 形式的には何も言ってなかったのです。

限量子を含まない閉論理式

0を空集合として、1 = {0}, Pow(1) = {0, 1} とします。0は偽を意味し、Fとも書きます。1は真を意味し、Tとも書きます。混乱の恐れがないなら、0を0, 1を1とも書きます。ほとんどの場合、0と0とF、1と1とTを区別しません -- こういうイイカゲンさ、ちゃらんぽらんさは、論理では当たり前のことなので、神経質になるのはやめましょう。

スコット・ブラケット（の値）を求めるときに使う公式（定義）を、コンテキストを省略して繰り返すと：

  • 〚A∧B〛 = 〚A〛∩〚B〛
  • 〚A∨B〛 = 〚A〛∪〚B〛
  • 〚¬A〛 = 〚A〛c （右肩のcは補集合をとることを表す）
  • 〚A⇒B〛 = 〚A〛c ∪〚B〛

記号 '⇒' を集合演算の意味でもオーバーロードして使うことにします。

  • （なんかの親集合の）部分集合 V, W に対して、 V⇒W := Vc ∪ W

この書き方を使うと：

  • 〚A⇒B〛 =〚A〛⇒〚B〛

左側の'⇒'は論理結合子、右側の'⇒'は集合演算です。こういうオーバーロード（記号の流用、多義的使用）は良くない（実害がある）習慣ですが、記号が足りないので現実には多用されます。ちゃらんぽらんで、悪いこともやってしまう、のが論理のやり口です。

では解答。一部（7番以降）は計算過程も示します。以下の論理式の場合、（記述が省略されているが）変数の変域を示すコンテキストは空。コンテキスト領域は1。したがって、スコット・ブラケットの値は0または1。念の為ここでは、0, 1 ではなくて 0, 1 を使います。

  1. 〚1 + 2 = 3〛 = 1
  2. 〚1 + 2 < 3〛 = 0
  3. 〚12 = 22〛 = 0
  4. 〚3 ≦ 5 ∧ 3 ≦ 3〛 = 1
  5. 〚1 + 2 < 3 ⇒ 12 = 22〛 = 1
  6. 〚1 + 2 < 3 ∨ 12 = 22 ∨ 3 ≦ 3〛 = 1
  7. 〚(3 ≦ 5 ∧ 3 ≦ 3) ⇒ 1 + 2 < 3〛 = 0
  8. 〚(3 ≦ 5 ∨ 3 ≦ 3) ⇒ ¬(1 + 2 < 3)〛 = 1
  9. 〚¬(1 + 2 < 3) ⇒ (1 + 2 = 2)〛 = 0
  10. 〚1 + 2 = 3 ⇒ (1 + 2 < 3 ⇒ 12 = 22)〛 = 1

計算過程：



7.

   〚(3 ≦ 5 ∧ 3 ≦ 3) ⇒ 1 + 2 < 3〛

 = 〚3 ≦ 5 ∧ 3 ≦ 3〛⇒〚1 + 2 < 3〛

 = (〚3 ≦ 5〛∩〚3 ≦ 3〛)⇒〚1 + 2 < 3〛

 = (1∩1)⇒0

 = 1⇒0

 = 1c∪0

 = 0∪0

 = 0
8.

   〚(3 ≦ 5 ∨ 3 ≦ 3) ⇒ ¬(1 + 2 < 3)〛

 = 〚3 ≦ 5 ∨ 3 ≦ 3〛⇒〚¬(1 + 2 < 3)〛

 = (〚3 ≦ 5〛∪〚3 ≦ 3〛)⇒〚1 + 2 < 3〛c

 = (1∪1)⇒0c

 = 1⇒1

 = 1c∪1

 = 0∪1

 = 1
9.

   〚¬(1 + 2 < 3) ⇒ (1 + 2 = 2)〛

 = 〚1 + 2 < 3〛c⇒〚1 + 2 = 2〛

 = 0c⇒0

 = 1⇒0

 = 1c∪0

 = 0∪0

 = 0
10.

   〚1 + 2 = 3 ⇒ (1 + 2 < 3 ⇒ 12 = 22)〛

 = 〚1 + 2 = 3 ⇒ (1 + 2 < 3 ⇒ 12 = 22)〛

 = 〚1 + 2 = 3〛⇒〚1 + 2 < 3 ⇒ 12 = 22〛

 = 〚1 + 2 = 3〛⇒(〚1 + 2 < 3〛⇒〚12 = 22〛)

 = 1⇒(0⇒0)

 = 1⇒1

 = 1

空なコンテキストの領域が1であることは、あまり深く考え込まないで、便宜的な約束だと思って受け入れましょう。この約束を受け入れれば、二値真偽値 {T, F} と、命題の真理集合（命題の外延、解集合、集合の内包的記法、デカルト解析幾何の意味での図形などと同じ）を、スコット・ブラケットにより統一的に扱うことができます。「便宜的」と言いましたが、この約束は実際は極めて整合的です。

限量子を含む閉論理式

解答を先に：

  1. 〚∀n∈N.(n ≧ 0)〛 = 1
  2. 〚∃n∈N.(n < 0)〛 = 0
  3. 〚∀n∈N.∃m∈N.(m ≧ n)〛 = 1
  4. 〚∀n∈N.∃m∈N.(m < n)〛 = 0
  5. 〚∀x∈R.∃y∈R.(y2 = x)〛 = 0 [追記 date="2018-12-07"]←間違っていた、修正しました。[/追記]
  6. 〚∀x∈R.∃y∈R.(x ≧ 0 ⇒ y2 = x)〛 = 1
  7. 〚∃y∈R.∀x∈R.(x ≧ 0 ⇒ y2 = x)〛 = 0
  8. 〚∀x∈R.∀y∈R.∃n∈N.((x ≧ 0 ∧ y > 0) ⇒ yn ≧ x)〛 = 1

これらの真偽値を理解するひとつの方法は、「命題と、そのコンテキスト／真理集合 (A8P6)」の追記に書いた「感情表現をタップリ混じえた日本語」に沿って考える方法です。

自然言語に基づく直感的理解も重要で、決して悪いものではありません。ですが、スコット・ブラケットは素朴集合論に基づいて定義されている関数なので、素朴集合論の観点からも理解しておいたほうがいいでしょう（次節以降／次回以降）。

反例と正例

反例という言葉はよく知られています。反例と対になる言葉はなんでしょう？ それは「例」です。しかし、「例」では、一般的な事例と区別が付かないので、テクニカルタームとして「正例」と呼ぶことにします。

コンテキスト付き論理式 (x∈X| A) があったとき、

  • 集合Xの特定の要素aが正例だとは、論理式Aの変数xにaを代入した後のスコット・ブラケット（の値） 〚A'〛 が1になること。A'は、Aの変数xにaを代入した後の閉論理式。
  • 集合Xの特定の要素aが反例だとは、論理式Aの変数xにaを代入した後のスコット・ブラケット（の値） 〚A'〛 が0になること。A'は、Aの変数xにaを代入した後の閉論理式。

正例集合は真理集合と同じであり、反例集合は真理集合の補集合です。また言葉が増えてしまいましたが、同じ意味です。

我々は、変数を持つ命題（＝コンテキスト付き命題）を、その正例や反例を通して理解します。つまり、命題の真理集合や、真理集合の補集合を使って考えるのです。“真理集合＝スコット・ブラケット”による“意味のモデリング”が、人間の思考とかけ離れているわけでもないでしょ。

限量子の数学的（素朴集合論的）解釈

限量された〈限量子付きの | quantified〉論理式とコンテキスト付き論理式は、相互に関連していて、切り離して議論は出来ません。

限量された論理式 ∀x∈X.P、∃x∈X.P のスコット・ブラケット（の値）を求めるには、限量子を外してコンテキストに換えた (x∈X| P) のスコット・ブラケットを先に求める必要があります。

  1. 〚∀x∈X.P〛 = 1 (⇔) 〚x∈X| P〛 = X
  2. 〚∀x∈X.P〛 = 0 (⇔) 〚x∈X| P〛 ≠ X
  3. 〚∃x∈X.P〛 = 1 (⇔) 〚x∈X| P〛 ≠ 0
  4. 〚∃x∈X.P〛 = 0 (⇔) 〚x∈X| P〛 = 0

ここで、記号 '(⇔)' は、メタな（つまり、普通の、形式化されてない）論理的同値の記号です。テクニカルタームとしての「正しい」と、テクニカルタームとしての「正例」を使って述べれば：

  1. ∀x∈X.P が正しい (⇔) (x∈X| P) が正しい
  2. ∀x∈X.P が正しくない (⇔) (x∈X| P) が正しくない
  3. ∃x∈X.P が正しい (⇔) (x∈X| P) が正例を持つ
  4. ∃x∈X.P が正しくない (⇔) (x∈X| P)が正例を持たない

テクニカルタームとしての「反例」「正例」を使えば：

  1. ∀x∈X.P が正しい (⇔) (x∈X| P) が反例を持たない
  2. ∀x∈X.P が正しくない (⇔) (x∈X| P) が反例を持つ
  3. ∃x∈X.P が正しい (⇔) (x∈X| P) が正例を持つ
  4. ∃x∈X.P が正しくない (⇔) (x∈X| P)が正例を持たない

限量された〈限量子付き〉の命題は、限量子を取り外したコンテキスト付き命題の、正しさの程度（＝スコット・ブラケットの値）を要約した表現と捉えられます。

補集合の性質、ついでに「メタ」について

正例の集合と反例の集合は、互いに補集合になっています。補集合は次の性質を持ちます。V, W をXの部分集合として：

  • V∪Vc = X
  • (Vc)c = V
  • (V∩W)c = Vc∪Vc
  • (V∪W)c = Vc∩Vc

これら補集合の性質は、排中律、二重否定、ド・モルガンの法則という論理法則の集合バージョンです。我々は、これらの論理法則とその集合バージョンを疑ったりしないし、平気で使います。他の数学の分野でも平気で使っているのだから、当然の話です。

そのことと、形式化された演繹システム内で、排中律、二重否定、ド・モルガンの法則などが成立するかどうかはまったくの別問題です。演繹システムは、我々が新しく作り出す（ソフトウェアプログラムと同様な）人工的構築物なので、下手に作れば期待される性質を持ちません。バグだらけのシステムだってありえます。

次の二文は、まったく別なことを述べています。メタ論理（我々が通常使っている形式化されてない論理）記号は丸括弧で包む規則で書きます。

  • メタ論理（我々が通常使っている形式化されてない論理）において、ド・モルガンの法則 (¬)(A(∧)B) (⇔) (¬)A(∨)(¬)B が成立しているし、既に平気で使っている。
  • 我々が構築した演繹システムSは、形式化されたド・モルガンの法則 "¬(A∧B) ⇔ ¬A∨¬B" を（なんらかのメカニズムにより）正しいと判断できる。

二番目の主張は、メタ命題（演繹システムSに関する普通の命題）であり、メタ論理（普通の論理）を使ってメタ証明（普通に証明）すべき事項です。

限量子を含む閉論理式の解説 (途中まで)

1. ∀n∈N.(n ≧ 0)

今まで述べたことから、次のような（メタな）同値性があります。

  • ∀n∈N.(n ≧ 0) が正しい (⇔) (n∈N| n ≧ 0) が反例を持たない
  • ∀n∈N.(n ≧ 0) が正しい (⇔) (n∈N| n ≧ 0) の反例集合が空
  • ∀n∈N.(n ≧ 0) が正しい (⇔) (n∈N| n ≧ 0) の正例集合がN
  • 〚∀n∈N.(n ≧ 0)〛 = 1 (⇔) 〚n∈N| n ≧ 0〛 = N

あるいは、

  • ∀n∈N.(n ≧ 0) が正しくない (⇔) (n∈N| n ≧ 0) が反例を持つ
  • ∀n∈N.(n ≧ 0) が正しくない (⇔) (n∈N| n ≧ 0) の反例集合が空ではない
  • ∀n∈N.(n ≧ 0) が正しくない (⇔) (n∈N| n ≧ 0) の正例集合がNではない
  • 〚∀n∈N.(n ≧ 0)〛 = 0 (⇔) 〚n∈N| n ≧ 0〛 ≠ N

これら同値な判定基準のどれを使ってもいいですが、例えば、「n ≧ 0 がN内で反例を持たない」ことから、〚∀n∈N.(n ≧ 0)〛 = 1 です。

2. ∃n∈N.(n < 0)
  • ∃n∈N.(n < 0) が正しい (⇔) (n∈N| n < 0) が正例を持つ
  • ∃n∈N.(n < 0) が正しい (⇔) (n∈N| n < 0) の正例集合が空ではない
  • ∃n∈N.(n < 0) が正しい (⇔) (n∈N| n < 0) の反例集合がNではない
  • 〚∃n∈N.(n < 0)〛 = 1 (⇔) 〚n∈N| n < 0〛 ≠ 0

あるいは、

  • ∃n∈N.(n < 0) が正しくない (⇔) (n∈N| n < 0) が正例を持たない
  • ∃n∈N.(n < 0) が正しくない (⇔) (n∈N| n < 0) の正例集合が空
  • ∃n∈N.(n < 0) が正しくない (⇔) (n∈N| n < 0) の反例集合がN
  • 〚∃n∈N.(n < 0)〛 = 0 (⇔) 〚n∈N| n < 0〛 = 0

前問と同じく、どれで判断しても 〚∃n∈N.(n < 0)〛 = 0 。


中途半端な場所ですが、続きは別な記事にします。続き → 問題集6の目的と解答と追加説明 その2 (A14R6-2) - 檜山正幸のキマイラ飼育記 メモ編

問題集1の目的と解答と追加説明 重要！ (A13R1)

RSS練習問題

※この記事は「記事13 解答1」

「だ・である調」から「です・ます調」に変更します。

問題集1とは、次の記事（の問題部分）のことです：

解答だけでなく、「どうしてこのような練習をするか？」や、関連する事項の説明もします。

内容：

  1. この問題は重要
  2. 解答
  3. 形式化された証明のだいたい

この問題は重要

「ノード・ワイヤー図と横棒記法の例と練習 (A2P1)」の問題は、証明の形式化の準備として最も重要な問題です。もしまだやってなかったら、是非にやってみてください。

「ノード・ワイヤー図と横棒記法の例と練習 (A2P1)」にも書いておいたように、こういう練習をしておかないと、証明の形式化がまったくピンと来ないでしょう。

形式化とは、我々生きている人間が現実世界で扱っているモノや行っているコトを、コンピュータでも扱えるデータやコンピュータでも実行できるアルゴリズムとして再定義することです。（次も参照。）

形式化された証明とは、ある種のデータをある種の基本コマンドだけで操作していく一連の過程です。コンピュータで動く演繹システムは、そのような過程を遂行することにより、人間の知的行為である証明をシミュレートします。ソフトウェアシステムではなくて、理論的に構築された概念的演繹システムでも事情は同じです。

我々は、演繹システムの挙動や能力を外から観測して調べるのですが、内部動作をある程度は自分で経験しておかないと、何の実感も湧かないでしょう。例えば、掛け算を遂行する電子回路の仕組みを理解するとき、自分自身はまったく掛け算した経験がないと無理がありますよね。

それと、竹内外史先生の言葉を思い出しましょう。

  • [論理／数学基礎論を]理解するに多大な煩わしさを経なければならない。

この「多大な煩わしさ」を事前に実感し、煩わしさに対する慣れと耐性を身につけるようにしましょう。

以下に解答です。解答の後に、より具体的な説明が書いてあります。

解答

Ins, Del, Fork, Merge, Add, Mult の操作だけを用いて、二元連立一次方程式 {2x - 3y + 1 = x - 2, x + y = 5} を解け。

解き方は色々ありますし、それらに優劣はありません。ここに書くのはあくまで一例です。

方針としては、2つの流れに分岐して、左側の流れでxを求め（yを消去し）、右側の流れでyを求めます（xを消去します）。テキストで書くのを楽にするため、左側と右側の操作が同じになるようにしました。中間で使った不要な等式を消して、最後に合流します。

「ノード・ワイヤー図と横棒記法の例と練習 (A2P1)」の最後の追記で述べたような略記を使います。

(1) 2x - 3y + 1 = x - 2
(2) x + y = 5
-------- Ins(-x - 1)
(1), (2)
(3) -x = -x
-------- Add(#1,#3)
(1) x - 3y = -3
(2) x +  y =  5
(3)
-------- Fork
(1),(2),(3)           (1),(2),(3)
-------- Ins(3)       -------- Ins(-1)
(1),(2),(3)           (1),(2),(3)
(4) 3 = 3             (4) -1 = -1
-------- Mult(#2, #-1)-------- Mult(#2, #-1)
(1) x - 3y = -3       (1) x - 3y = -3
(2) 3x + 3y = 15      (2) -x - y = -5
(3),(4)               (3),(4)
-------- Add(#1, #2)  -------- Add(#1, #2)
(1) 4x = 12           (1) -4y = -8
(2),(3),(4)           (2),(3),(4)
-------- Ins(1/4)     -------- Ins(-1/4)
(1) 4x = 12           (1) -4y = -8
(2),(3),(4)           (2),(3),(4)
(5) 1/4 = 1/4         (5) -1/4 = -1/4
-------- Mult(#1, #-1)-------- Mult(#1, #-1)
(1) x = 3             (1) y = 2
(2),(3),(4),(5)       (2),(3),(4),(5)
-------- Del(#-1)     -------- Del(#-1)
(1),(2),(3),(4)       (1),(2),(3),(4)
-------- Del(#-1)     -------- Del(#-1)
(1),(2),(3)           (1),(2),(3)
-------- Del(#-1)     -------- Del(#-1)
(1),(2)               (1),(2)
-------- Del(#-1)     -------- Del(#-1)
(1) x = 3             (1) y = 2
-------- Merge
(1) x = 3
(2) y = 2
横棒記法による図をノード・ワイヤー図にせよ。

描画方向は、先の横棒記法の図をそのまま写し取った↓→（上から下、左から右）です。


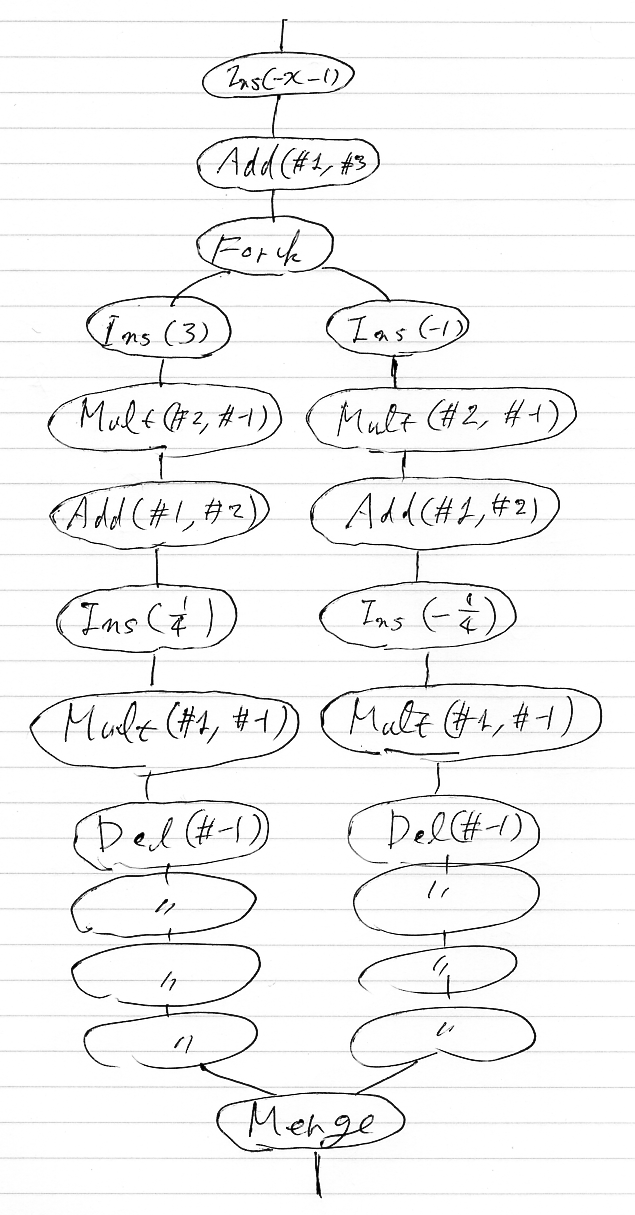
前問のノード・ワイヤー図を、すべての描画方向（↑→, ↑←, ↓→, ↓←, →↑, →↓, ←↑, ←↓）で描いてみよ。

この解答は省略しますが、このテのトレーニングが必要なことは、次の記事をザッと眺めてみてください。内容を理解する必要はありません。眺めるだけ。

前問のノード・ワイヤー図をテキスト記法で表現せよ。
  • Ins(-x - 1);Add(#1,#3);Fork;(Ins(3)\otimesIns(-1));(Mult(#2, #-1)\otimesMult(#2, #-1));(Add(#1, #2)\otimesAdd(#1, #2));(Ins(1/4)\otimesIns(-1/4));(Mult(#1, #-1)\otimesMult(#1, #-1));(Del(#-1)\otimesDel(#-1));(Del(#-1)\otimesDel(#-1));(Del(#-1)\otimesDel(#-1));(Del(#-1)\otimesDel(#-1));Merge

[追記 date="2018-12-07"]↑最後のMergeが抜けていたので追加。[/追記]

ひとつの図に対するテキスト記法も、ひと通りではありません。図のクラスター分割〈ブラケティング〉により、対応するテキスト記法も変わります。このことについては、「ノード・ワイヤー図〈ストリング図〉 (A1) // グルーピング〈ブラケティング〉と描き換え」をもう一度見てください。

もし可能なら、…

これは実際にやってみる話。「自分以外の人」の代わりに「時間がたった自分」でやってみるとよいでしょう。

解き方（出来上がる図）は一通りではない。違った解き方も考えよ。

唯一の正解はないので、他もやってみてください。

適当な二元連立一次方程式に対して、上の問題群と同じ作業を行え。

必要があれば追加の練習をしましょう。

形式化された証明のだいたい

二元連立一次方程式 {2x - 3y + 1 = x - 2, x + y = 5} を解く一連の過程を図示したノード・ワイヤー図〈ストリング図〉では、等式系（縦に等式を並べたもの）をラベルするのは煩雑なので省略しました。省略しないで、等式系も記入すると次のようになります。

四角の枠は、ノードではなく、ワイヤーラベルを記入するための枠です。これを、ラベルフレーム、または単にフレームと呼びます。ノードは水色に塗ってあります。

ノードラベルがテキストではなくて再びノード・ワイヤー図であれば、例えば（単なる一例）、次のような図になるでしょう。

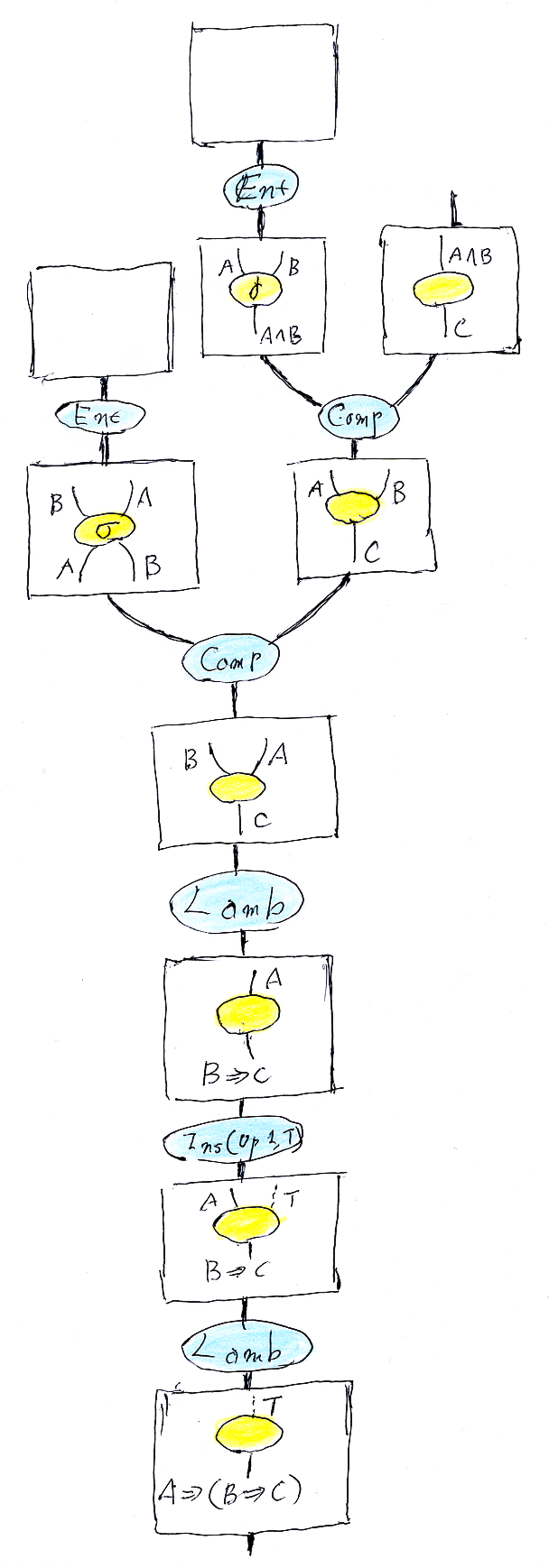
今、この図を理解する必要はありません。しかし、次のことは知っておいてください。

  • 形式化された証明を分かりやすく図示するには、この程度の絵が必要になる。これでも、相当に省略していて、もっと細部を描き込むとさらに複雑になる。
  • 良心的な著者・編集者・出版社が、十分なゼニ（予算）をかければ、このような絵をふんだんに使った教科書を作れるだろう。
  • さらに十分なゼニ（予算）があれば、ラベルフレームをアニメーションのフレームとした、マルチスクリーン（同時に複数のシーンを映し出す）アニメーションムービーを制作できるだろう。
  • さらにもっとゼニ（予算）があれば、アニメーションムービーの制作環境や対話的な再生環境（プレイヤー）も作れるだろう。
  • 現実には、それだけの手間・コストをかけることは、ほぼ不可能。

次善の策として、横棒記法を使ってみます。

  1. ラベルフレーム内の黄色のノードは一本棒の横線にする。
  2. 水色のノードは二本棒の横線にする。
  3. 何も描いてない白いフレームは☆で示す。
              ☆
            ====== Ent
             A  B       A∧B
             ----γ    -----
   ☆        A∧B        C
 ====== Ent ================= Comp
  B  A          A  B
  ----σ        -----
  A  B           C
 ===================== Comp
         B  A
        -----
          C
      ========= Lamb
          A
        ------
         B⇒C
      ========= Ins(up 1, T)
         A T
        ------
         B⇒C
      ========= Lamb
          T
       ---------
       A⇒(B⇒C)

入れ子の内側の横棒記法の図をシーケント形式（「シーケントに親しもう (A11P9)」参照）に直せば、横幅が広がりますが、縦方向は節約できます。

                                  ☆
                         ================== Ent
         ☆               A, B -(γ)→ A∧B   A∧B → C
 ================== Ent =============================== Comp
  B, A -(σ)→ A, B          A,  B → C
 ======================================== Comp
      B, A → C
     ============ Lamb
      A → B⇒C
     ============ Ins(up 1, T)
      A, T → B⇒C
     ================= Lamb
       T → A⇒(B⇒C)

さらに実際に使われている図では：

  1. 一本棒をもう使ってないので、二本棒を一本棒にする。
  2. ☆のようなマーカーは置かないで空白にする。
  3. → の左にTだけがあるときは、何も書かない。（この規則は、リストの種類を明示的に示す我々の流儀では使えない。）

他にも、絵の情報（幾何的／グラフ理論的な情報）を、イラストなしの通常文字組版で印刷可能にするための工夫が色々とあります。しかし、そのような制約と工夫（苦し紛れの方便）が、本来は簡単なものを、非常に煩雑にしてしまっている事実があります。興味があれば、次の本編記事も参照してください。

ともかくシーケントなんだから、頼むよ、皆んな (A12)

RSS練習問題

※この記事は「記事12」

シーケントは論理の中核的な概念であり、演繹システムを構成するにしろ、意味論を考察するにしろ、シーケントを基本的対象物とみなすことなる（そうするのが、現状では最良の選択肢だと思われる）。

「シーケントとは何であるか？」という問に、「シーケントとはシーケントである」と答えるのが最も正確で安全なんだけど、それじゃー身も蓋もない。不正解さと誤解される危険を免れないが、シーケント周辺の余計な話を書いておく。「ちゃんとロンリする」際の必須のツールであるシーケントで挫折されては困るから。

※ 今回、練習問題はありません。が、問題意識についてはたくさん書いてます。

内容：

  1. ゲンツェンのLKシーケント計算をご存知の方への注意
  2. 定理記述としてのシーケント
  3. 形式化とシーケント
  4. 演繹システムへの意志を持ち続けること
  5. シーケントから、その先へ

ゲンツェンのLKシーケント計算をご存知の方への注意

検索などでたまたまここに辿り着いた人が誤解するのも困るので、毎回この節を冒頭に置くことにする。

  1. '⇒'は含意〈条件法〉の論理結合子で、'→'がシーケントの左右を区切る記号である。
  2. ゲンツェンのLKシーケントでは、左辺のカンマは連言的に、右辺のカンマは選言的に解釈をする。ここでのシーケントでは、出現位置の情報を使わずに、カンマは常に連言的であり、選言的な区切り記号に縦棒'|'を使う。
  3. (x∈R, n∈N) のような書き方は、集合論の命題ではなくて、自由変数の型宣言（のリスト）である。自由変数の型宣言のリストをコンテキストと呼ぶ。
  4. 暗黙のコンテキストを使う場合もあるが、できるだけ、シーケント内に明示的にコンテキストを書き込むようにしている。

定理記述としてのシーケント

シーケントの用途としては、まずは定理の記述に使えることは分かるだろう。

例えば、因数分解できれば2次方程式が解けることの根拠は、次の“定理”だと言えるだろう。



実数 a, b に対して、

実数 x に対して、

(x - a)(x - b) = 0 だとする。

これらから

  x = a

または

  x = b

が出る。

英語風だと、



For a, b∈R

For x∈R

Given (x - a)(x - b) = 0

Holds

  x = a

Or

  x = b

End

そしてシーケントは：

  • (a, b∈R), (x∈R), (x - a)(x - b) = 0 → x = a | x = b

自然数の引き算は出来るときと出来ないときがあるが、出来るのは次の“定理”があるからだろう。



自然数 n, m に対して、

n ≦ m だとする。

これらから

  ∃k∈N.(n + k = m)

が出る。

英語風だと、



For n, m∈N

Given n ≦ m

Holds

  ∃k∈N.(n + k = m)

End

そしてシーケントは：

  • (n, m∈N), n ≦ m → ∃k∈N.(n + k = m)

2次方程式の判別式が正ならば、（異なる）2つの解が存在することを主張する“定理”なら、いきなりシーケントで：

  • (a, b, c∈R), ¬(a = 0), b2 - 4ac > 0 → ∃s, t∈R.( ¬(s = t) ∧ (as2 + bs + c = 0) ∧ (at2 + bt + c = 0) )

フェルマー／ワイルズの“定理”なら：

  • (n∈N), n ≧ 3 → ¬∃x, y, z∈N.(xn + yn = zn)

形式化とシーケント

「命題」「定理」「証明」などの言葉は、現実世界で生きた人間が行う行為・活動としての数学のなかで使われる言葉である。現実世界で生きた人間が行う数学的行為・活動の一部をコンピューターで動作するソフトウェアシステムで実現しようとすると、「命題」「定理」「証明」などを、コンピューターが処理可能なデータとコンピューターが実行可能なアルゴリズムとして記述しなくてはならない。

我々現実世界に生活している人間達の言葉・概念を、コンピューターが扱えるナニカとして再定義する行為を形式化〈formalize〉と呼ぶ。「命題」に関しては、論理記号を使った論理式として満足できる形式化が出来ている。よって、「命題」という言葉は、コンピューターが扱えるナニカとしての意味でも使ってよい。

前節で「“定理”」という書き方をしていたが、これには理由がある。そう、形式化が済んでない。現時点において、

  • 形式化された命題 → 論理式として形式化が済んでいる
  • 形式化された定理 → よく分からない
  • 形式化された証明 → よく分からない

シーケントは、構文的形式〈syntactic form〉としては文句なく定義されている〈well-defined〉。命題と命題のリスト（連言的リストと選言的リスト）が定義されているなら、リストを左右に並べた形式がシーケントなのだから、文句の付けようがない。コンピューターが扱えるデータとしてシーケントを実装することも容易だ。興味ある人のために（ない人はスキップ）、TypeScriptによる*1データ型定義を書いておこう。

// 論理式
// それなりに複雑なツリー構造になる
// めんどくさいから省略
type Formula = /* ダミーとして文字列、うそぴょーん */string;

// 単一の型宣言
type TypeDecl = {
    varName: string,
    typeName: string// 本格的にしたいなら、型名ではなくて type expression
};

// コンテキスト ＝ 型宣言のリスト(配列ともいう)
type Context = Array<TypeDecl>;

// 連言的(conjunctive)か選言的(disjunctive)かの識別マーク
enum Junctive {
    CONJ,
    DISJ
};

// 連言的か選言的かマークされた、
// コンテキストと論理式が混じったリスト
// シーケントの左辺はこの形
type MarkedMixedList = {
    // 識別マーク
    mark: Junctive,
    // コンテキストと論理式が混じったリスト
    mixedList: Array<Context | Formula>
};

// 連言的か選言的かマークされた、
// 論理式のリスト
// シーケントの右辺はこの形
type MarkedList = {
    // 識別マーク
    mark: Junctive,
    // 論理式のリスト
    list: Array<Formula>
};

// シーケント
type Sequent = {
    left: MarkedMixedList,
    right: MarkedList
};

「シーケントとはシーケントである」とは、シーケントと呼ばれる構文形式に我々生きている人間がどのような思い〈感情〉を抱くかに関係なく、演繹システムが扱うデータとして文句なく定義されている〈well-defined〉のだから、それでいいだろう、ということだ。

シーケントの形式的定義については、次の記事を参照。

「シーケントとは定理の記述形式である」は、人間に対する説明としては悪くないが、演繹システム内における形式化された定理がよく分かんない現状では、形式的には（演繹システムに関する話題としては）なにごとも言ってない。演繹システムの外の世界＝我々が生きているこの世界における、雰囲気的・気分的な人間同士でしか通用しない他愛も無い語りに過ぎない。

演繹システムへの意志を持ち続けること

我々の目的は、演繹システムの外の世界＝我々が生きているこの世界における、雰囲気的・気分的な人間同士でしか通用しない他愛も無い語りを繰り広げることではない。人工的な演繹システムを構成し、その性質・能力を調べることである。この目的のために、心理的な状態を整備するために、人間同士のコミュニケーションとして、目的に至る手段として、他愛も無い語りを繰り広げることはあるだろうし、実際、今、それをしている。

演繹システムをどう作ろうか？ 演繹システムはどんな性質・能力を持つんだろうか？ という話では、雰囲気的・気分的な他愛も無い語りは何の意味も持たない。完全に形式化された正確な議論だけをし続けなくてはならない。これはけっこうシンドイ作業なのだ。

シンドイので、馴染みがあり楽ちんな我々が生きているこの世界における、雰囲気的・気分的な人間同士でしか通用しない他愛も無い語りへと逃げたい誘惑にかられる。あるいは、いつのまにか雰囲気的・気分的な他愛も無い語りをしてしまう。

例えば、「x + y ≧ 0」という命題は正しいだろうか？ 「正しくない気がする」としたら、正しくない根拠は何か？ 実際には正しくないのではなくて、単に解釈ができない。変数x, y の変域を明示して、

  • (x, y∈N) → x + y ≧ 0

なら正しい。しかし、

  • (x, y∈R) → x + y ≧ 0

なら正しくない。だが、条件（仮定）を足して、

  • (x, y∈R), x ≧ 0, y ≧ 0 → x + y ≧ 0

なら正しい。

今出したシーケント (x, y∈R), x ≧ 0, y ≧ 0 → x + y ≧ 0 が正しい理由・根拠が「正しいような気がするから」だとしたら、「俺は正しくないよう気がするから正しくないぞ」に対抗できない。

数理的な議論において、素朴集合論を信頼し、素朴集合論の内部で正当化できることは認めようというコンセンサスは得られている。「正しいような気がするから」ではなくて、テクニカルタームとしての「正しい」として、素朴集合論の内部で正当化できる定義と計算法を提示できるならば、もはや雰囲気的・気分的な語りではなくて、数理的な議論の一部になる。

実際に、命題の形式化であるところの論理式に対して、その正しさ（の程度）を出力する関数としてスコット・ブラケットを定義して、スコット・ブラケットの値により「正しさ」は定義している。論理式は構文的対象物〈syntactic object〉であり、その全体は（素朴集合論で認められる）集合となり、スコット・ブラケットはその集合を域〈domain〉として、適当な集合Xのベキ集合Pow(X)を余域〈codomain〉とする関数である（Xはコンテキストの領域なので、コンテキストに応じてXも変化する）。

素朴集合論で認められる集合、写像、集合演算、集合の比較などを使って「正しさ」を定義したのなら、その「正しさ」概念は、「素朴集合論の内部で正当化できることは認めようというコンセンサス」のもとで正当かつ正確な意味を持ち、雰囲気的・気分的な語りではなくなる。

我々が、演繹システムを、理論的な構築物として、あるいは実際にコンピューターで動くソフトウェアとして実現しようとするとき、その入力データや内部処理データが何であるかが分からないでは話にならない。そこで、論理式、論理式のリスト、シーケントなどを、「素朴集合論の内部で正当化できることは認めようというコンセンサス」に合致する形で定義する必要があった。

仮に我々が、演繹システムを作ったとして、その挙動が期待通りかどうかをテストするとき、「システムの応答が期待通りか、期待外れか」を、システムの外部にいる我々が判断できなかったらどうにもならない。「なんか、うまく動いているような気がする」「いや、どうも奇妙な感じが俺はする」じゃ埒が明かない。その話を昨日「シーケントに親しもう」の後半でした。

シーケントから、その先へ

シーケント概念を十分に説明したわけではないが、シーケントという構文的対象物を定義して、ベキ集合に値をとる関数であるスコット・ブラケットも定義する必要性・必然性があったことは、ある程度は同意いただけたろう。

しかし、「定理」も「証明」も形式化が全然出来てない。現時点では、「定理」「証明」などの言葉はインフォーマルに（人間同士のコミュニケーションにおいて雰囲気的・気分的に）しか使えない。今後、「定理」や「証明」を形式的に扱うためのデータ構造やアルゴリズム（処理方式）を、「素朴集合論の内部で正当化できることは認めようというコンセンサス」に合致する形で定義していくことになる。雰囲気的・気分的な語りでお茶を濁すわけにはいかない。

※注意： 実際には、「定理」「証明」という言葉は形式化しないかも知れない。理由は、形式化された定理、形式化された証明の意味があまりにもバラバラ色々すぎるので、使わないのが無難と思われるから。「推論」「リーズニング」という言葉を選んで形式化すると思う、たぶん。

*1:TypeScriptの型定義構文は、かつて僕等が作っていた某システムの構文とあまりにも似ていて、僕には書きやすい。

シーケントに親しもう (A11P9)

RSS練習問題

※この記事は「記事11 問題集9」

記号的表現に対して「自然言語（日本語や英語）による読み下しが出来ないと馴染めない」という事情も当然だから、シーケントの読み下し練習をする。そして、「“シーケントの正しさ”を正しく判断する／判断できる」とはどういうことか？ を（できれば）納得して欲しい。問題を解きながらストーリーを追い、出来るだけリアルにシリアスに状況をイメージしてくださいな。

他の練習問題をする前に、この記事をザッと読んだほうがいいかも知れない。
[追記]続きの記事があります。

[/追記]

内容：

  1. ゲンツェンのLKシーケント計算をご存知の方への注意
  2. シーケントを読み下そう
  3. 疑問文を作ろう
  4. その疑問文に、誰がどのように答えるのか？
  5. 演繹システムの格付け作業はどう行うか？

ゲンツェンのLKシーケント計算をご存知の方への注意

検索などでたまたまここに辿り着いた人が誤解するのも困るので、毎回この節を冒頭に置くことにする。

  1. '⇒'は含意〈条件法〉の論理結合子で、'→'がシーケントの左右を区切る記号である。
  2. ゲンツェンのLKシーケントでは、左辺のカンマは連言的に、右辺のカンマは選言的に解釈をする。ここでのシーケントでは、出現位置の情報を使わずに、カンマは常に連言的であり、選言的な区切り記号に縦棒'|'を使う。
  3. (x∈R, n∈N) のような書き方は、集合論の命題ではなくて、自由変数の型宣言（のリスト）である。自由変数の型宣言のリストをコンテキストと呼ぶ。
  4. 暗黙のコンテキストを使う場合もあるが、できるだけ、シーケント内に明示的にコンテキストを書き込むようにしている。

シーケントを読み下そう

左辺が連言的リストで右辺が唯一つの論理式からなるシーケントだけを扱う。この形だけでも実用性は十分にある。この種のシーケントの形は、α1, ..., αn をコンテキスト、Γ1, ..., Γn を連言的リストとして、

  • α1, Γ1, ..., αn, Γn → B

例えば、

  • (n∈N), ∃k∈N.(n = 2k), n ≦ 10, (a∈R), (x∈R), T → ∃y∈R.(yn = a2)

この例では：

  1. コンテキスト α1 に相当するのは、コンテキスト (n∈N)
  2. 連言的リスト Γ1 に相当するのは、連言的リスト ∧(∃k∈N.(n = 2k), n ≦ 10)
  3. コンテキスト α2 に相当するのは、コンテキスト (a∈R)
  4. 連言的リスト Γ2 に相当するのは、空な連言的リスト ∧()
  5. コンテキスト α3 に相当するのは、コンテキスト (x∈R)
  6. 連言的リスト Γ3 に相当するのは、（長さが1の）連言的リスト ∧(T)
  7. 命題 B に相当するのは、命題 ∃y∈R.(yn = a2)

冒頭に書いた制限「左辺が連言的リストで右辺が唯一つの論理式からなるシーケントだけを扱う」から、リストは常に連言的なので、単にリストと書いたら連言的リストとする。つまり、カンマは論理ANDと解釈してよい。

シーケントを、英語ベースの自然言語風の書き方にするルールは：

  1. コンテキストの前に For を付ける。
  2. 左辺に登場する論理式のリストの前に Given を付ける。
  3. 矢印の代わりに Holds で区切る。
  4. 右辺の論理式を書いて、End で終わる。
  5. 空コンテキストや空リストに関する記述は省略してよい。



For α1

Given Γ1

 …

For αn

Given Γn

Holds

  B

End

実例：



For n∈N

Given ∃k∈N.(n = 2k), n ≦ 10

For a∈R

For x∈R

Given T

Holds

 ∃y∈R.(yn = a2)

End

シーケントを、日本語ベースの自然言語風の書き方にするルールは：

  1. コンテキストは、「型 変数名 に対して、」と書く。変数が複数あるときは、「型1 変数名1 と 型2 変数名2 に対して、」のように「と」で繋ぐ。
  2. 左辺に登場する論理式のリストの後に 「だとする。」を付ける。
  3. 矢印の代わりに 「これらより、」で区切る。「ら」が不自然なときは「これより、」でもよい。
  4. 右辺の論理式を書いて、「が出る。」 で終わる。
  5. 空コンテキストトや空リストに関する記述は省略してよい。



自然数 n に対して、

∃k∈N.(n = 2k), n ≦ 10 だとする。

実数 a に対して、

実数 x に対して、

T だとする。

これらより、

 ∃y∈R.(yn = a2)

が出る。

英語風／日本語風に書いたシーケントが内容的に正しいか正しくないかはとりあえず置いといて、形としては、定理のステートメント〈主張〉のように読めるだろう。

問題： 以下にあげるシーケントに対して、α1, Γ1, ..., αn, Γn, B に相当する部分がどんなコンテキスト、リスト、論理式であるかを明確にせよ（先の例のように）。
問題： 以下にあげるシーケントを、英語ベースの自然言語風の書き方に直せ。英語として多少不自然になるのは致し方ない。
問題： 以下にあげるシーケントを、日本語ベースの自然言語風の書き方に直せ。日本語として多少不自然になるのは致し方ない。

シーケント：

  1. (x∈R, y∈R), x ≧ 0, y ≧ 0 → x + y ≧ 0
  2. (x∈R, y∈R), x ≧ 0, y ≦ 0, (n∈N), T → xn + yn ≧ 0
  3. (x∈R, y∈R), (n∈N) → xn + yn ≧ 0
  4. (x∈R, y∈R), x ≧ 0, y ≦ 0, (n∈N), ∃k∈N.(n = 2k) → xn + yn ≧ 0
  5. (x∈R, y∈R), (n∈N), ∃k∈N.(n = 2k) → xn + yn ≧ 0
  6. (x∈R, y∈R, n∈N), ∃k∈N.(n = 2k) → xn + yn ≧ 0
  7. (x∈R, y∈R, n∈N) → ∃k∈N.(n = 2k) ⇒ xn + yn ≧ 0
  8. (x∈R, y∈R) → ∀n∈N.(∃k∈N.(n = 2k) ⇒ xn + yn ≧ 0)

疑問文を作ろう

Aが命題のとき、「Aは正しいか？」という疑問文は意味を持つ。シーケントは、定理のステートメントを形式化したものと考えよう。すると、シーケントψに対して「ψは正しいか？」という疑問文も意味を持つだろう -- 誰かが、ψ（で表現される）ステートメントを主張したとき、「彼の主張は正しいか？」という疑問文は意味を持つのだから。

この状況にリアリティを持たせるために、シーケントが正しいかどうかを問う疑問文を実際に作ってみる。

英語風：

  1. 英語ベースの自然言語風の書き方の場合は、シーケント（の英語風表現）全体を引用符で囲む。
  2. Is "……" correct? という疑問文を作る。

日本語風：

  1. 日本語ベースの自然言語風の書き方の場合は、シーケント（の日本語風表現）全体を鉤括弧で囲む。
  2. 「……」は正しいか？ という疑問文を作る。

例：



英語風：

Is "For n∈N Given ∃k∈N.(n = 2k), n ≦ 10 For a∈R For x∈R Given T Holds  ∃y∈R.(yn = a2) End" correct?



日本語風：

「自然数 n に対して、∃k∈N.(n = 2k), n ≦ 10 だとする。実数 a に対して、実数 x に対して、T だとする。これらより、 ∃y∈R.(yn = a2) が出る。」は正しいか？

問題: 前節の8個のシーケントに対して、そのシーケントは正しいか？ という疑問文を英語風／日本語風で作成せよ。

その疑問文に、誰がどのように答えるのか？

コンテキストは α, β など、単一の論理式は A, B など、論理式のリスト（ここでは連言的リスト）は Γ〈大文字ガンマ〉, Δ〈大文字デルタ〉などで表す。シーケントは小文字ギリシャ文字の後のほう、ψ〈小文字プサイ〉, φ〈小文字ファイ〉 などを使う。ふー、文字種が足りない。

シーケントψが与えられたとき、「ψは正しいか？」という疑問文に誰が答えるかに関して、ニ通りのケースを想定する。

  • ケース1: 我々、現実世界に生きている人間、私（檜山）やあなたが答える。
  • ケース2: ソフトウェアシステムが答える。

ケース2、ソフトウェアシステム（架空のものかも知れない）に答えさせることを考える。シーケント（のデータ）を入力すると、それが正しいかどうかを判断して答えるソフトウェアシステムが10種あるとする。それぞれ S1, S2, ..., S10 とする。

ソフトウェアシステムに入力するために、1000個のシーケントを準備する。ψ1, ψ2, ..., ψ1000 としよう。

ソフトウェアシステムの優劣を格付けするために次の基準を設ける。

  1. 1000個のシーケントすべての正しさを正しく判定した場合は「優」ランクとする。
  2. 1000個のシーケントのうち950個以上の正しさを正しく判定した場合は「良」ランクとする。
  3. 1000個のシーケントのうち800個以上の正しさを正しく判定した場合は「可」ランクとする。
  4. 1000個のシーケントのうち800個未満の正しさしか正しく判定できなかった場合は「不可」ランクとする。

ソフトウェアシステムではなくて、中にいる小人さんや妖精さんが答えてくれるシステムでもかまわない。要は、現実世界に生きて暮らしている我々人間以外が判断主体となる人工的または仮想的（おとぎ話的）なシステムならよい。

演繹システムの格付け作業はどう行うか？

10個の演繹システム（ソフトウェアシステム、または小人さん・妖精さんの世界）S1, S2, ..., S10 を格付けしよう。もし「優」ランクのシステムがあれば、それは実用に耐えるだろう。「良」ランクでも使えなくはない（けっこう間違うが）。「可」でもいい人がいるかも知れない。「不可」は間違えすぎだ。

格付けのテストが終わると（終わればね）、例えば（例えばね）次のような結果が出るかもしれない。

  • S1 不可
  • S2 可
  • S3 不可
  • S4 良
  • S5 不可
  • S6 不可
  • S7 不可
  • S8 優
  • S9 可
  • S10 不可

演繹システム達が出す結果を我々人間が評価するためには、事前に1000個のシーケントの正しさを我々人間が知っていなくてはならない。そうでないなら格付けできない。ここで、ケース1がどうしても必要になる。

  • ケース1: 我々、現実世界に生きている人間、私（檜山）やあなたが答える。

次の1000個の疑問文に、現実世界に生きている我々人間が先に答えを出しておく必要がある。

  • Is "ψ1" correct?
  • Is "ψ2" correct?
  • Is "ψ3" correct?
  • ...
  • Is "ψ999" correct?
  • Is "ψ1000" correct?

現実世界に生きている我々人間が判断する方法とは、つまり、いつもどおりに普通に数学を使って判断することである。集合やら写像やらをいつもどおりに普通に利用して考えるだろう。霊感に頼ったり、サイコロを振っては決めないはず。

人工的または仮想的な演繹システムを調べる前に、「シーケントの正しさ」という概念を、現実世界に生きている我々人間が雰囲気ではなく確実に理解できる形で普通に定義しておく必要がある。演繹システム達は我々の評価（格付け）の対象であり、事前に信用できる保証など何もない。だから、次の“普通の定義”がある。

  • シーケントψが正しい とは ψのスコット・ブラケット（の値）〚ψ〛が、ψのコンテキストαの領域 Dom(α) と一致することである。

ここで出てくるスコット・ブラケットは、特殊な括弧記号を使っているが、普通の方法で定義可能な関数である。例えば、Scottのような関数名を使ってもよい（凹レンズ括弧を使うのは単なる習慣だから）。

スコット・ブラケット、あるいは関数Scottの定義は以下のとおりである。

与えられたシーケントψのコンテキストを左端にまとめる（シーケントの正規化）。まとめた後のψ'は

  • α, Γ → B

という形にできる。αはコンテキスト、Γは論理式のリスト、Bは論理式である。与えられたシーケントψ、正規化されたシーケントψ'に対して、

  • Scott(ψ) := Scott(ψ')
  • Scott(ψ') = 〚ψ'〛 = 〚α, Γ → B〛 := 〚α| Γ〛c ∪〚α| B〛

ここで：

  1. ψ'は α, Γ → B という正規化後のシーケントのこと。
  2. Scottはスコット・ブラケットの関数名
  3. 〚α| Γ〛は、コンテキストαのもとでの論理式のリストΓのスコット・ブラケット
  4. 右肩のcは部分集合の補集合をとる集合演算
  5. ∪は、部分集合の合併をとる集合演算
  6. 〚α| B〛は、コンテキストαのもとでの論理式Bのスコット・ブラケット

上の定義内で論理式のリストに対するスコット・ブラケットが必要になるが：

  • 〚α| Γ〛 = 〚α| A1, ..., An〛 := 〚α| A1〛∩ ... ∩〚An〛

ここで：

  1. 〚α| A1〛は、コンテキストαのもとでの論理式A1のスコット・ブラケット
  2. 〚α| An〛は、コンテキストαのもとでの論理式Anのスコット・ブラケット。その他も同じ。
  3. ∩は、部分集合の共通部分をとる集合演算

結局、単一の論理式に対するスコット・ブラケットに帰着される。その基本的な場合のスコット・ブラケットは、

リンク先の問題を解くときは、経験と直感に頼ってもよい。が、単一の論理式に対するスコット・ブラケットの定義を、普通の数学内で厳密に書くことができる（「正しさ」「正しさの程度」を哲学的・理念的に語ったりはしない！）。

スコット・ブラケットという関数の定義が厳密に書けることと、その関数がアルゴリズム的に計算可能なことは別問題である。数学における関数の定義は、計算手順を伴うわけではないから。

また、格付けテスト用のデータである ψ1, ψ2, ..., ψ1000 は、我々人間が事前に正しいかどうかを確認済みでないと格付けテストに使えないが、全く勝手に与えられたシーケント φ に対して、正しいかどうかを常に我々が判定できるとは言ってない。

  • 我々人間と同じ能力を持つシステムSがあれば、Sは「優」ランクとなる。
  • 我々人間と同じ能力を持つシステムSがあれば、テストに使うシーケント数がいくら増えても、常に人間と同じ答えを出す（はず）。
  • 我々人間と同じ能力を持つ（と想定される）システムSは、事前に我々人間が確認してないシーケントφを勝手に与えられたとき、シーケントφが正しいかどうかを常に判定できるのだろうか？
  • 我々人間と同じ能力を持つ（と想定される）システムSが、勝手に与えられたシーケントψが正しいかどうかを常に判定できるのなら、我々人間もまた、勝手に与えられたシーケントが正しいかどうか判定できることになる。Sに出来て人間に出来ないはずはない。

[追記]続きの記事があります。

[/追記]