問題集6の目的と解答と追加説明 その2 (A14R6-2)
※この記事は「記事14 解答6-2」
問題集6とは、次の記事(の問題部分)のことです:
「その1」は、次の記事です。
内容:
- 書き方の注意
- 限量子を含む閉論理
- コンテキスト付き論理式
- コンテキスト付き論理式(続き)
- コンテキストの水増し
- 様々な論理式を作ってみる
- 限量子も使ってみる
書き方の注意
次の書き方の約束は、あまり(ほとんどかも)使っていません。
- メタ論理(形式されてない通常の論理)の論理記号は丸括弧で囲む。(∧), (⇒) など。
- 形式化された命題である論理式は引用符で囲む。"∀x∈R.∃y∈R.(y2 = x)" のように。
形式化されている/されてないを特に強調したいときは、気まぐれに使います。
限量子を含む閉論理
前回は、「限量子を含む閉論理」の途中まででした。解答を再掲すると:
- 〚∀n∈N.(n ≧ 0)〛 = 1
- 〚∃n∈N.(n < 0)〛 = 0
- 〚∀n∈N.∃m∈N.(m ≧ n)〛 = 1
- 〚∀n∈N.∃m∈N.(m < n)〛 = 0
- 〚∀x∈R.∃y∈R.(y2 = x)〛 = 0
- 〚∀x∈R.∃y∈R.(x ≧ 0 ⇒ y2 = x)〛 = 1
- 〚∃y∈R.∀x∈R.(x ≧ 0 ⇒ y2 = x)〛 = 0
- 〚∀x∈R.∀y∈R.∃n∈N.((x ≧ 0 ∧ y > 0) ⇒ yn ≧ x)〛 = 1
3番以降は、限量子が2つ付いています。「命題と、そのコンテキスト/真理集合 (A8P6)」の追記に書いた「感情表現をタップリ混じえた日本語」に沿って考えれば、おそらく解答は得られるでしょう。
しかし、2個以上の限量子が付いた形式化された論理式の数学的解釈は、日本語としての解釈とは別に定義する必要があります。なぜなら、形式化された論理式は人工的に定めた構文的なデータに過ぎず、我々人間が意味を定義してあげないと、天然の意味などないからです。
「意味を定義してあげる」作業は、国語辞典の項目を書き下す作業ではありません。「問題集6の目的と解答と追加説明 (A14R6-1)」において、1個の限量子に対してやったのと同程度の精度の議論が必要です。が、これはちょっとめんどうなので、オプショナルな(必須ではない)別記事にします(短い解説なら、この記事の最後にあります)。
コンテキスト付き論理式
- (x∈R| x < 0 ∨ 1 < x)
- (x∈R| 0 < x ∧ x < 1)
- (x∈R| 0 < x ∧ 1 < x)
- (x∈R| x < 0 ⇒ x2 = 1)
- (x∈R| x2 = 1 ⇒ x < 0)
- (x∈R| x2 = 1 ⇒ x = 0)
- (x∈R| x2 = 1 ⇒ x = 1)
- (x∈R| x2 = 1 ⇒ (x = 1 ∨ x = -1))
- (x∈R| (x2 = 1 ∧ x ≧ 0) ⇒ x = 1)
- (x∈R| (x2 = 1 ∧ x ≧ 0) ⇒ (x = 1 ∨ x = -1))
- (x, y∈R| x2 + y2 = 1)
- (x, y∈R| x2 + y2 = 4 ∧ x + y ≧0)
- (x, y∈R| x2 + y2 = 4 ∧ x + y ≧ -1)
- (x, y∈R| x2 + y2 = 1 ∨ x + y = 0)
- (x, y∈R| x2 + y2 = 1 ⇒ x = 1)
- (x, y∈R| x = 1 ⇒ x2 + y2 = 1)
- (x, y∈R| (x = 1 ∧ y = 0) ⇒ x2 + y2 = 1)
- (x, y∈R| x2 + y2 = 1 ⇒ x + y ≦ 2)
- (x, y∈R| x2 + y2 = 1 ⇒ x + y ≦ 1)
- (x, y∈R| x2 + y2 ≦ 1 ⇒ x + y ≦ 2)
- (x, y∈R| x2 + y2 ≦ 1 ⇒ x + y ≦ 1)
- (x, y∈R| (x2 + y2 ≦ 1 ∧ x + y ≦ 0) ⇒ x + y ≦ 1)
1から10のスコット・ブラケットを図示すると次のようです。コンテキスト領域は、R = 直線 で、赤い所がスコット・ブラケットの値(真理集合)です。赤くない所は真理集合の補集合、つまり反例集合です。

実数の区間を、閉区間 [a, b] 、開区間 (a, b) のように書くと:
- 〚x∈R| x < 0 ∨ 1 < x〛 = (-∞, 0)∪(1, +∞)
- 〚x∈R| 0 < x ∧ x < 1〛 = (0, 1)
- 〚x∈R| 0 < x ∧ 1 < x〛 = (1, +∞)
- 〚x∈R| x < 0 ⇒ x2 = 1〛 = {-1}∪[0, +∞)
- 〚x∈R| x2 = 1 ⇒ x < 0〛 = (-∞, 1)∪(1, +∞)
- 〚x∈R| x2 = 1 ⇒ x = 0〛 = (-∞, -1)∪(-1, 1)∪(1, +∞)
- 〚x∈R| x2 = 1 ⇒ x = 1〛 = (-∞, -1)∪(-1, +∞)
- 〚x∈R| x2 = 1 ⇒ (x = 1 ∨ x = -1)〛 = (-∞, +∞)
- 〚x∈R| (x2 = 1 ∧ x ≧ 0) ⇒ x = 1〛 = (-∞, +∞)
- 〚x∈R| (x2 = 1 ∧ x ≧ 0) ⇒ (x = 1 ∨ x = -1)〛 = (-∞, +∞)
含意'⇒'を含む (x∈X| A⇒B) の形のコンテキスト付き論理式のスコット・ブラケットを求めるときは、いちいち悩まないで定義どおりに計算します。
- 〚x∈X| A⇒B〛 = 〚x∈X| A〛c∪〚x∈X| B〛
例えば、"(n∈N| nは偶数 ⇒ n2は偶数)" のスコット・ブラケットならば:
〚n∈N| nは偶数 ⇒ n2は偶数〛
= 〚n∈N| nは偶数〛c∪〚n∈N| n2は偶数〛
= {n∈N| nは奇数}∪{n∈N| n2は偶数}
ここで、{n∈N| nは奇数}が真理集合に入ってますが、これを真理集合に入れないと、奇数の集合は真理集合の補集合、つまり反例の集合になってしまいます。奇数が反例なのではなくて、
- 偶数であって、その二乗は偶数ではない自然数
が反例です。
反例ではない自然数は正例、つまり真理集合=スコット・ブラケットに入ります。コンテキスト領域(今の場合はN)の要素は、必ず正例か反例のどちらかです。「正例でも反例でもない」とか「正例でもあり反例でもある」なんて要素は在りません! 「Yesとも言えるしNoとも言える」なんて答え方は、まったく許されないのです。
※注意: 「nは偶数」は日本語ですが、"∃k∈N.(n = 2k)" とすれば形式化された命題になります。全部を形式化した形にすると長くなるので、一部を非形式的に日本語で書く略記はしばしば使います。定式化や理論構成自体は厳密でも、説明や表現はとても雑でエエカゲンなんです。
コンテキスト付き論理式(続き)
問題11から15の図は次のようになります。13は間違っていたので、後から描きなおしています。コンテキスト領域は、R×R = R2 = 平面 で、赤い所がスコット・ブラケットの値(真理集合)です。赤くない所は真理集合の補集合、つまり反例集合です。
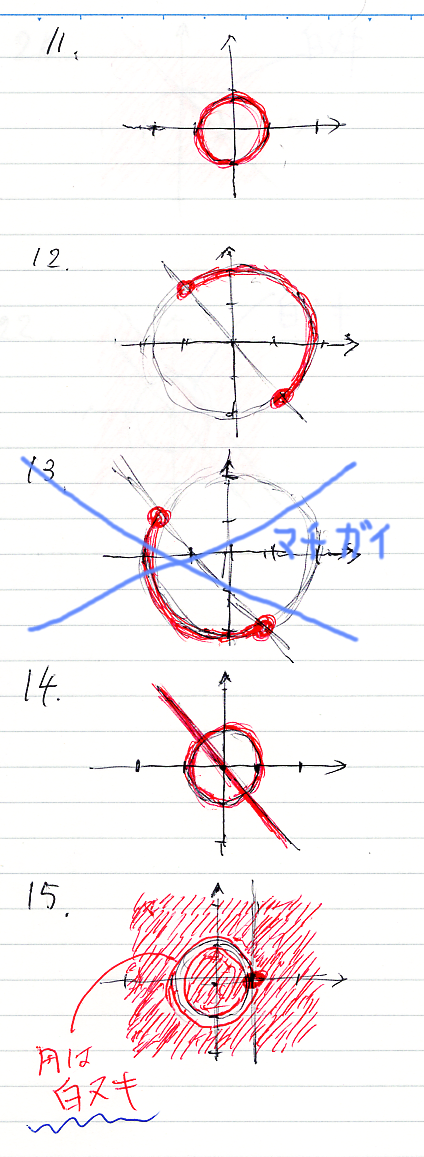
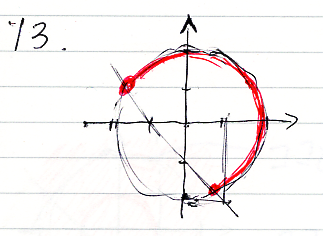
15は汚いですが、円周が白ヌキ(補集合、反例)です。が、点 (1, 0)は赤(正例)です。
続いて、16から22まで。
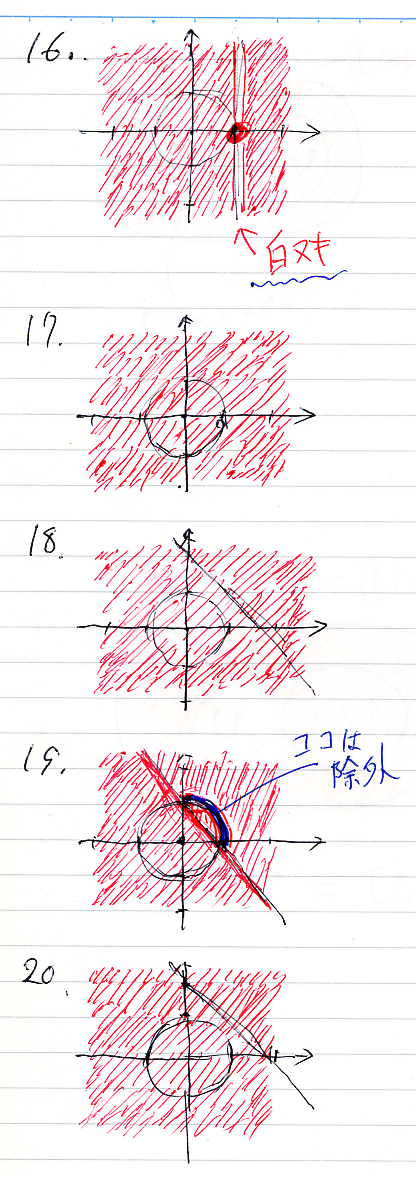
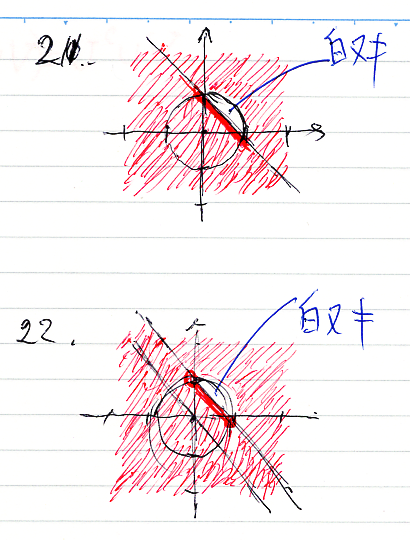
19は青で塗っちゃいましたが、白ヌキ(補集合、反例)のつもりです。
コンテキストの水増し
- (x, y∈R| x < 0 ∨ 1 < x)
- (x, y∈R| 0 < x ∧ x < 1)
- (x, y∈R| 0 < x ∧ 1 < x)
- (x, y∈R| x < 0 ⇒ x2 = 1)
- (x, y∈R| x2 = 1 ⇒ x < 0)
- (x, y∈R| x2 = 1 ⇒ x = 0)
- (x, y∈R| x2 = 1 ⇒ x = 1)
- (x, y∈R| x2 = 1 ⇒ (x = 1 ∨ x = -1))
- (x, y∈R| (x2 = 1 ∧ x ≧ 0) ⇒ x = 1)
- (x, y∈R| (x2 = 1 ∧ x ≧ 0) ⇒ (x = 1 ∨ x = -1))
もとのスコット・ブラケット(真理集合)は、直線内の区間(の寄せ集め)なので、それを上下方向に無限に伸ばした平面領域を描きます。例えば2番なら、幅1で縦方向に無限に長い帯です。
- (x, y∈R| 1 + 2 = 3)
- (x, y∈R| 1 + 2 < 3)
- (x, y∈R| 12 = 22)
- (x, y∈R| 3 ≦ 5 ∧ 3 ≦ 3)
- (x, y∈R| 1 + 2 < 3 ⇒ 12 = 22)
- (x, y∈R| 1 + 2 < 3 ∨ 12 = 22 ∨ 3 ≦ 3)
- (x, y∈R| (3 ≦ 5 ∧ 3 ≦ 3) ⇒ 1 + 2 < 3)
- (x, y∈R| (3 ≦ 5 ∨ 3 ≦ 3) ⇒ ¬(1 + 2 < 3))
- (x, y∈R| ¬(1 + 2 < 3) ⇒ (1 + 2 = 2))
- (x, y∈R| 1 + 2 = 3 ⇒ (1 + 2 < 3 ⇒ 12 = 22))
- (x, y∈R| ∀n∈N.(n ≧ 0))
- (x, y∈R| ∃n∈N.(n < 0))
- (x, y∈R| ∀n∈N.∃m∈N.(m ≧ n))
- (x, y∈R| ∀n∈N.∃m∈N.(m < n))
- (x, y∈R| ∀x∈R.∃y∈R.(y2 = x))
- (x, y∈R| ∀x∈R.∃y∈R.(x ≧ 0 ⇒ y2 = x))
- (x, y∈R| ∃y∈R.∀x∈R.(x ≧ 0 ⇒ y2 = x))
- (x, y∈R| ∀x∈R.∀y∈R.∃n∈N.((x ≧ 0 ∧ y > 0) ⇒ yn ≧ x))
もとの(水増しする前の)コンテキスト領域は1で、スコット・ブラケット(真理集合)が0か1だったので:
- もとのスコット・ブラケットが1ならば、平面全体
- もとのスコット・ブラケットが0ならば、空集合
様々な論理式を作ってみる
まず、命題パラメータ A, B, C に代入する具体的な論理式を選びます。
- A として20番を選ぶ: (x, y∈R| 0 < x ∧ x < 1)
- B として31番を選ぶ: (x, y∈R| x2 + y2 = 4 ∧ x + y ≧ -1)
- C として29番を選ぶ: (x, y∈R| x2 + y2 = 1)
この設定で次の論理式のスコット・ブラケット(真理集合)を描きます。赤い所がスコット・ブラケットの値(真理集合)です。赤くない所は真理集合の補集合、つまり反例集合です。
- ¬A
- A∧B
- A∨B
- A⇒B
- A⇒¬B
- (A∧B)⇒C
- (A∨B)⇒C
- A⇒B∧C
- A⇒B∨C
- (A∧B)∨C
こんな(↓)感じ。描く順番がアッチャコッチャ。
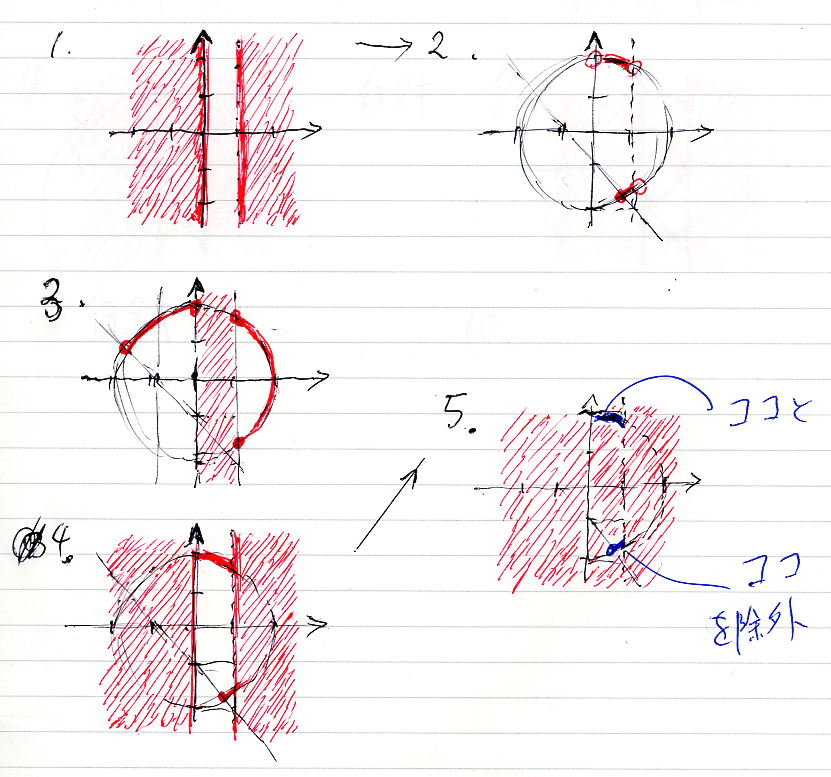
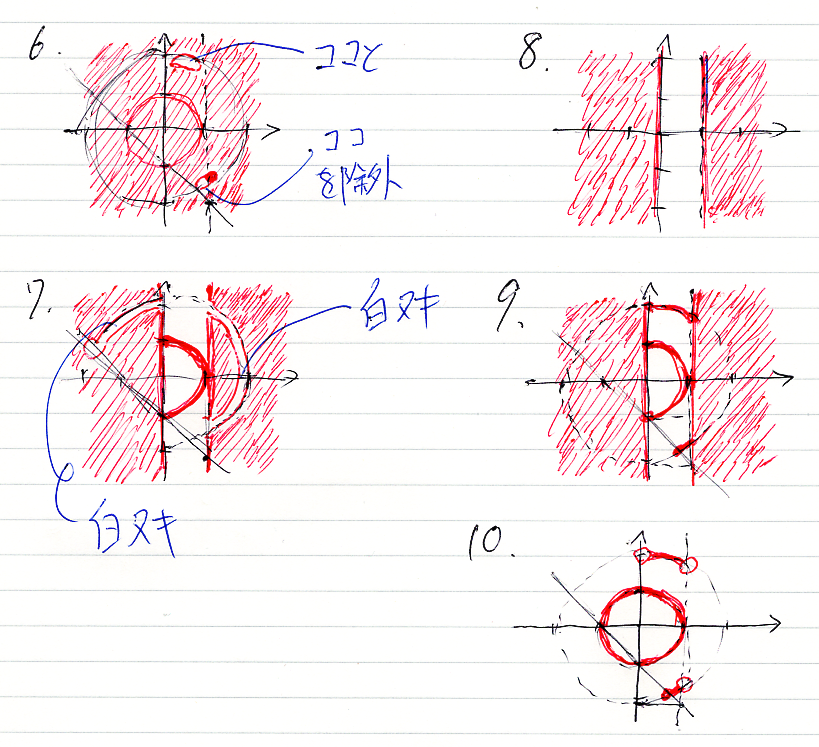
限量子も使ってみる
Aに何を選んでもあまり面白い絵にならないので絵は割愛。
- ∀x.A
- ∀y.A
- ∀x.∀y.A
- ∃x.A
- ∃y.A
- ∃x.∃y.A
- ∀x.∃y.A
- ∀y.∃x.A
一般に、限量子が付いた場合のスコット・ブラケットの描き方を説明しておきます。
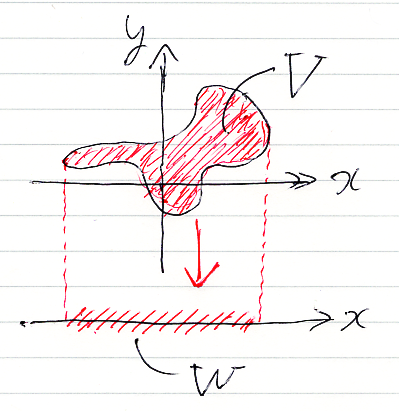
〚x∈R, y∈R| A〛は、コンテキスト領域R2内の部分集合(平面内の図形)なので、それをVと置きます。存在命題のスコット・ブラケット〚x∈R| ∃y∈R.A〛は、集合Vを射影した像です。上の図で射映像はWとなっています。
- W = (Vの射影像) = 〚x∈R| ∃y∈R.A〛
全称命題 ∀y∈R.A に関しては、
- ∀y∈R.A と ¬∃y∈R.¬A は論理的に同値
という結果を使って、
- (Vcの射映像)c = 〚x∈R| ∀y∈R.A〛
これらは、∃y∈R.A と ∀y∈R.A のスコット・ブラケットを計算するときの公式(定義)と思ってもかまいません。つまり、(x∈R, y∈R| A) のスコット・ブラケットが分かれば、それから、∃y∈R.A と ∀y∈R.A のスコット・ブラケットは素朴集合論内で定義・計算が出来るわけです。