絵図の描き方と省略法 (A16)
※この記事は「記事16」
次の問題はやってみましたか?
解答(の一例)は次の記事にあります。
引き続く次の記事も類似の問題です。
どれも、「絵図を描きましょう」という問題です。練習で描いたような絵図は、人間が目視できるだけでなく、コンピュータにとっても扱いやすいんです。コンピュータのメモリ内に展開するデータとして、ツリー構造やグラフ構造を表現することは容易です。したがって、絵図の操作(変形や組み合わせ)は、データを処理するアルゴリズムとして定式化できます。(興味があれば、「ともかくシーケントなんだから、頼むよ、皆んな (A12) // 形式化とシーケント」も参照。)
この記事では、完全な絵図とその省略(節約)図法について、オハナシとして述べます。オハナシですから、細部が理解できなくても気にすることはありません。今は、証明の形式化への(心の)準備として読んで、後でまた細部まで確認するのがよいでしょう。
内容:
- 絵図を完全に描く
- テキストによる表現
- 省略法
絵図を完全に描く
「ノード・ワイヤー図と横棒記法の例と練習 (A2P1)」の問題に出したノード・ワイヤー図を、ノード・ラベルである等式系も省略せずに描くと次のようでした(「問題集1の目的と解答と追加説明 重要! (A13R1)」の図を再掲)。
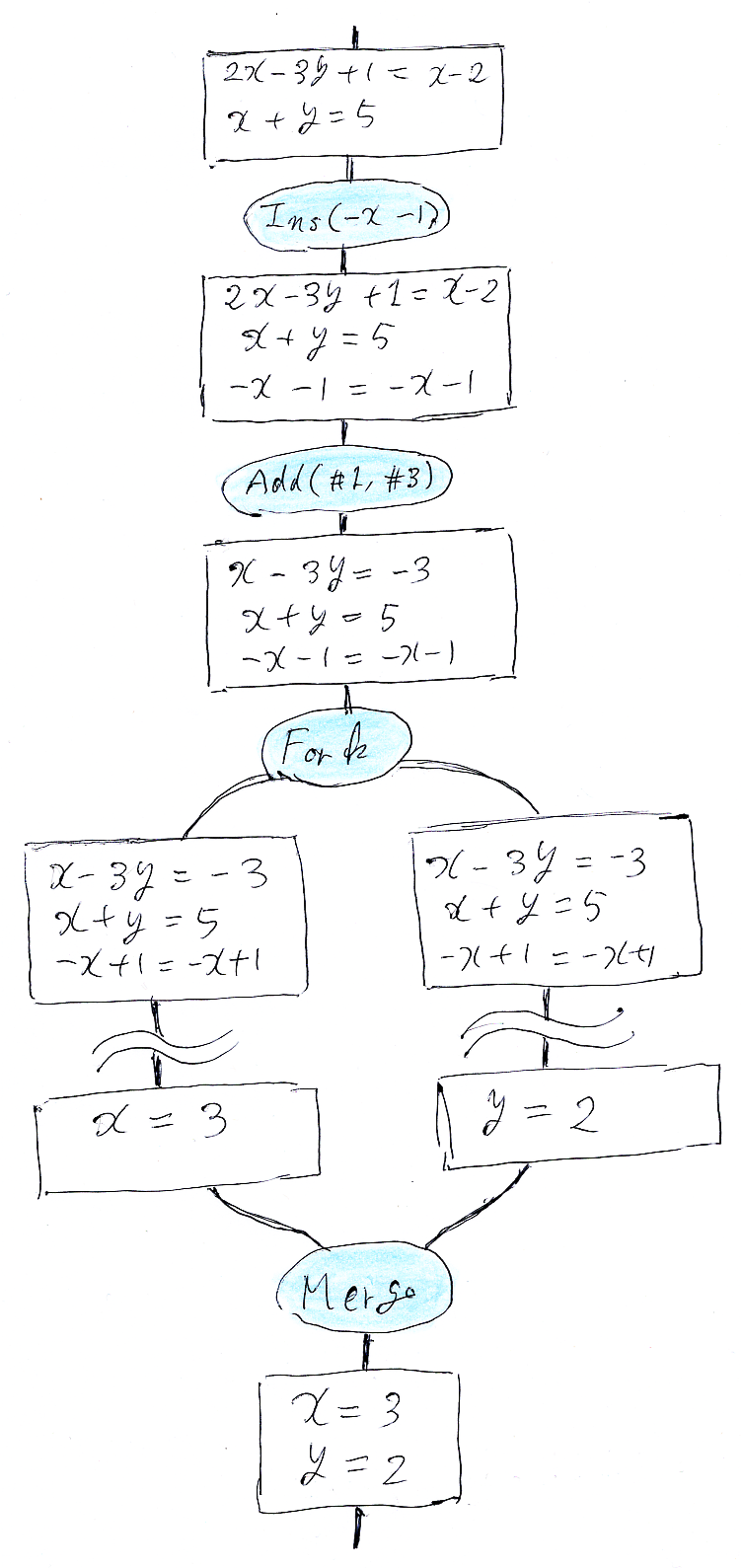
この図をテキスト(文字)でなんとか表現するには横棒記法を使います。
2x - 3y + 1 = x - 2
x + y = 5
---------------------- Ins(-x - 1)
2x - 3y + 1 = x - 2
x + y = 5
-x - 1 = -x - 1
-------------------- Add(#1,#3)
x - 3y = -3
x + y = 5
-x - 1 = -x - 1
---------------------------------- Fork
x - 3y = -3 x - 3y = -3
x + y = 5 x + y = 5
-x - 1 = -x - 1 -x - 1 = -x - 1
〜〜〜〜〜〜〜〜 〜〜〜〜〜〜〜〜〜
〜〜〜〜〜〜〜〜 〜〜〜〜〜〜〜〜〜
x = 3 y = 2
-------------------------- Merge
x = 3
y = 2「問題集1の目的と解答と追加説明 重要! (A13R1)」で出したもうひとつの絵図に関して次のように書きました。
形式化された証明を分かりやすく図示するには、この程度の絵が必要になる。これでも、相当に省略していて、もっと細部を描き込むとさらに複雑になる。
同じ図を、今度は省略なしで描いてみます。
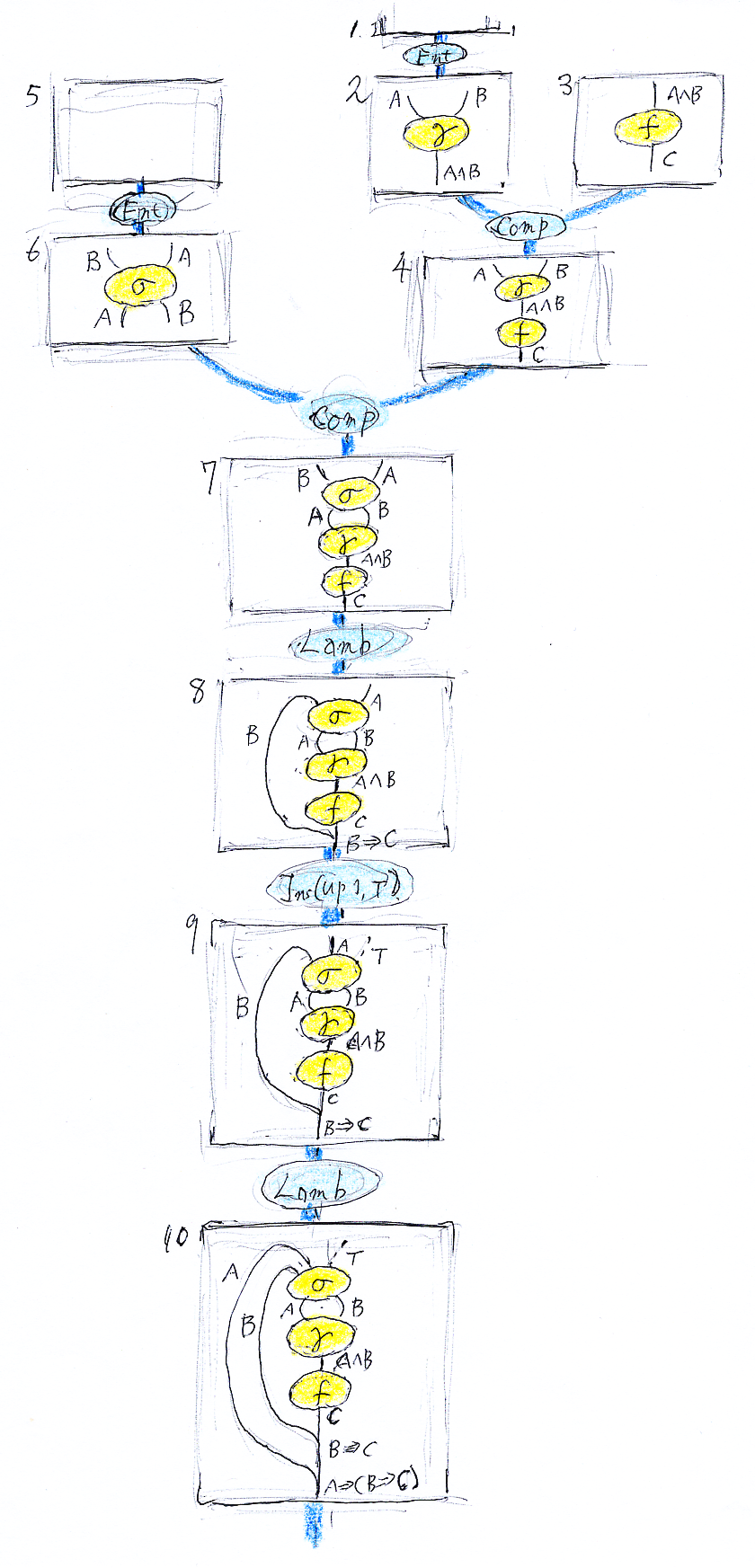
テキストによる表現
前節の図(二番目のほう)は、ワイヤーラベルとしてノード・ワイヤー図が付いているので、結果的に入れ子のノード・ワイヤー図になります。ワイヤーラベルを入れるラベルフレーム(四角い枠)内にノード・ワイヤー図が描いてあります。
8番と番号が付いたフレーム内の絵を見てみます。
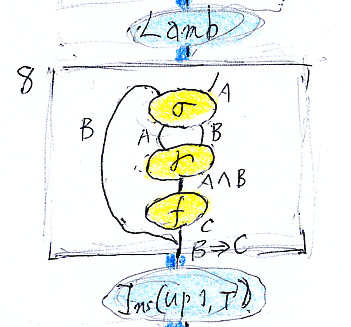
左側にBとラベルされた曲がったワイヤーがあります。この絵を、次のような横棒記法で書いては、曲がったワイヤーの情報が抜けてしまいます。
B A
---------- σ
A B
---------- γ
A∧B
------- f
C
-------
B⇒C曲がったワイヤーをテキストで表現する方法はいくつかありますが(実情は、みんなそれぞれ勝手な表記を使っている)、例えば、次のようにして曲がったワイヤーを表すことができます。
#1
-----
B A
---------- σ
A B
---------- γ
A∧B
------- f
C
------- ∩(#1)
B⇒C上の'#1'は番号付けで、下の'∩(#1)'は、#1から出た曲がったワイヤーがここで合流することを示す目印です。この記法を使って、入れ子のノード・ワイヤー図を横棒記法にしましょう。空白のフレームは'☆'で表します。
☆
========= Ent
A B A∧B
------ γ ------ f
☆ A∧B C
======== Ent ===================== Comp
B A A B
------ σ ------ γ
A B A∧B
------ f
C
================================ Comp
B A
------- σ
A B
------ γ
A∧B
------ f
C
============================ Lamb
#1
----
B A
-------- σ
A B
-------- γ
A∧B
----- f
C
----- ∩(#1)
B⇒C
============================ Ins(up 1, T)
#1
----
B A T
----------- σ
A B
-------- γ
A∧B
----- f
C
----- ∩(#1)
B⇒C
============================ Lamb
#1 #2
---- ---
B A T
------------- σ
A B
-------- γ
A∧B
----- f
C
----- ∩(#1)
B⇒C
--------- ∩(#2)
A⇒(B⇒C)イラストが使えない場合でも、省略無しで完全な入れ子横棒記法の図を使うなら、証明の形式化はかなり簡単です -- 難しくはありません。ただし、とても手間と紙面(紙の面積)を要することにはなります。
※注意: 次の図は実際は不正確で、Tが上に乗れば、もはやσではありません。σ以外のラベルを使ったほうがいいのですが、Tが乗っただけでいちいちラベルを変えるのも面倒だったので、同じσでラベルしています。これも、ことを分かりにくくする略記ではありますが。
B A T
----------- σ
A B省略法
手間と紙面を節約するために、絵図を省略して描く方法があります。しかし、省略すれば分かりにくくなります。「手間と紙面」と「分かりやすさ」はトレードオフの関係にあり、大幅な省略をした記法は難解です。
代表的な省略法は二種で:
- 「最後の一枚だけ」で済ます方法
- 「プロファイルだけ」で済ます方法
「最後の一枚」は、先の例で言えば、次の図だけを提示する方法です。
#1 #2
---- ---
B A T
------------- σ
A B
-------- γ
A∧B
----- f
C
----- ∩(#1)
B⇒C
--------- ∩(#2)
A⇒(B⇒C)簡単な場合は「最後の一枚」だけでも何とかなりますが、過程が複雑になると、最後の一枚だけでそれに至る過程を想像するのは困難です。過程を想像するヒントとして注釈を入れたりしますが、その注釈の入れ方のルールを考えたり覚えたりする手間が増えます(本末転倒な感じ)。
フレーム内のノード・ワイヤー図のプロファイルとは、入力列と出力列の仕様です(入力列/出力列に関しては「整数式の操作 (A3P2)」)。プロファイルは、「入力列 → 出力列」という、シーケントの形になります。
先の例を、「プロファイルだけ」方式で書いてみます。
☆
============== Ent
☆ A, B → A∧B A∧B → C
============== Ent ============================== Comp
B, A → A, B A, B → C
======================================= Comp
B, A → C
============================ Lamb
A → B⇒C
============================ Ins(up 1, T)
A, T → B⇒C
============================ Lamb
T → A⇒(B⇒C)入門段階では「最後の一枚」方式、より進んだ学習では「プロファイルだけ」方式が使われる傾向があります。どちらがいいか?という議論はあまり意味がありません。どちらも良くないので。
完全な絵図を実際に描いてみること、省略されても完全な絵図をイメージできるように今後トレーニングすることが重要です。
「手間と紙面 vs. 分かりやすさ」というトレードオフでは、ほとんど常に「分かりやすさ」を犠牲にして「手間と紙面」を節約する選択肢が採用されます。コストという深刻な要因があるので致し方ないのですが、論理の啓蒙と普及にとっては、大変に悲劇的な事態です。
事態が変わるには、30年、50年という時間がかかるでしょう。興味があれば、次の本編記事をどうぞ。