整数式の構文解析木 (A4P3)
※この記事は「記事4 問題集3」
ノード・ワイヤー図〈ストリング図〉の解説は:
これより前に行うべき練習は:
今回も、「整数式の操作」で定義した整数式を扱う。諸々の定義や記法も、「整数式の操作」から引き継ぐ。整数式の構文解析木〈parse tree〉を紹介し、その応用として、整数式の構成過程〈construction process〉をふたつの部分に分ける。
構文解析木は、単に練習問題の題材ではない。符号化/コンパイルを定義する際に、構文解析木が本質的に使われる。木〈ツリー〉は、最も重要なデータ構造と言ってよい。
内容:
- 構文解析木
- 練習問題: 構文解析木
- 構文解析木から横棒記法の図へ
- 練習問題: 横棒記法
- 式の構成図と構文解析木
- 練習問題: 構成図
- セットアップと演算子導入
- 練習問題: セットアップと演算子導入
- IXY記法
- 練習問題: IXY記法
構文解析木
式 2x と -z を次のような図に描くことがある。
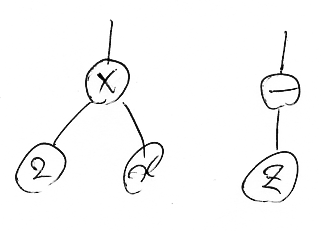
2x は 2×x なので、掛け算の二項演算子 × を上の位置に描いて、その下に 2 と x をぶら下げる。同様に、単項演算子である -(マイナス記号、負号)を上の位置に描いて、その下に z をぶら下げれば、-z の図。
このような描き方のルールを繰り返し適用すると、(2x + -z) + 10 は次の図で表現できる。
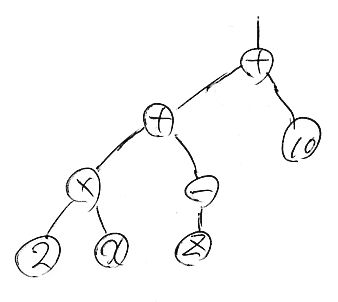
このような図を整数式の構文解析木〈parse tree〉と呼ぶ。
構文解析木はノード・ワイヤー図の一種で:
- 末端のノードラベルは、非負整数か変数の文字。
- 末端以外のノードラベルは演算子記号(+, ×, -)。
- ワイヤーラベルは書かなくてよい。書きたいなら、注釈として中間の式(部分式、subexpression)を書いてもよい。(参考:型つき〈typed〉の式では、ワイヤーラベルに型を書く。)
- 描画方向は ↑→ 。
練習問題: 構文解析木
次の整数式の構文解析木を描け。
- a + (2b + -1)
- ((2x + -z) + 10) + (a + (2b + -1))
- (6 + a)t
- -(xx)
- (6 + a)t + -(xx)
- y2 + x2
- x + -x
- (x2 + 2(xy)) + y2
- (a + b) + c
- a + (b + c)
- ((a + b) + c)(a + (b + c))
- 2s2 + -(2s) + -2
構文解析木を描く練習問題は、自分でいくらでも作れるので、必要があれば追加の問題をやって、概念と描き方に慣れる。
構文解析木から横棒記法の図へ
構文解析木はノード・ワイヤー図なので、横棒記法の図に描き換えることができる。構文解析木の描画方向が↑→なので、横棒記法の図も↑→で描くことにする。つまり、段を下から上に昇るように読む。慣れ親しんだ上から下ではないので注意。ただし、上から下に向かって“分解していく”とは読める。
描き換えの方法は次図の例を見れば明らかだろう。
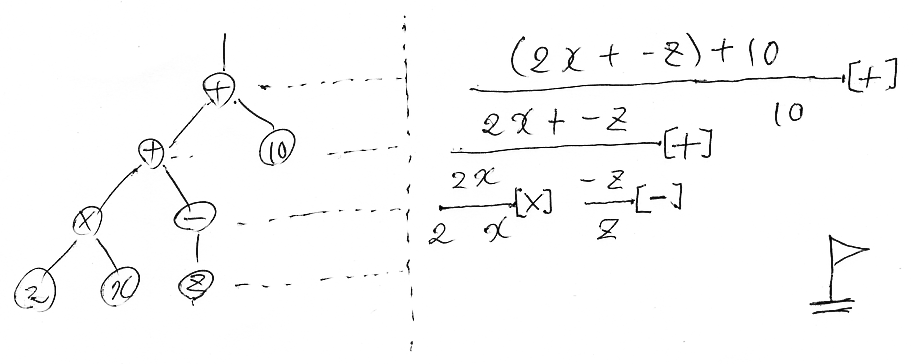
演算子記号の'-'と横棒の'-'がまぎれないように、演算子は角括弧で囲むことにした。
(2x + -z) + 10
---------------------[+]
2x + -z 10
---------------[+]
2x -z
------[×] -----[-]
2 x z練習問題: 横棒記法
「練習問題: 構文解析木」の整数式を、すべて横棒記法の図で描け。描画方向は↑→。
式の構成図と構文解析木
「整数式の操作」で描いたような、整数式がどのようにして組み立てられるかを示した図を、式の構成図〈construction diagram〉と呼ぶことにする。構成の際に使われる基本操作は、sum, prod, opp, dup, swap, id である。
式の構文解析木は、次の変形で式の構成図になる。
- 描画方向を、↑→ から ↓→ に変更する。
- ラベルを、'+'から'sum', 'prod'から'×', '-'から'opp' へと書き換える。
構文解析木では、dup, swap, id 操作は使われない。
練習問題: 構成図
「練習問題: 構文解析木」、「練習問題: 横棒記法」で描いた構文解析木を、描画方向とラベルを変更することにより、構成図に描き換えよ。 図法は、ノード・ワイヤー図でも横棒記法の図でもどっちでも(あるいは両方描いても)よい。以下、図法の指定がないときは、好きにしてよい。
セットアップと演算子導入
「整数式の操作」において、x, y |→| y2 + x2 という入出力を持つ構成図として次の図を挙げた。
x y ----- dup ----- dup x x y y ------ prod ------ prod xx yy --------------- swap yy xx ---------- sum yy + xx
この図の描画方向とラベルを変更してみる。
yy + xx ----------[+] yy xx ---------------[swap] xx yy ------[×] ------[×] x x y y -----[dup] -----[dup] x y
swap, dup が混じっているので、構文解析木にはならない。yy + xx の構文解析木は、
yy + xx ------------[+] yy xx ----[×] ----[×] y y x x
構文解析木の入出力は、y, y, x, x |→| y2 + x2 なので、入出力が食い違っている。この違いを解消するには、x, y |→| y, y, x, x という構成図を作ればよい。例えば、次の図がその例である(描画方向が↑→であることに注意)。
y y x x -----[dup] -----[dup] y x -------------[swap] x y
入出力が x, y |→| y, y, x, x であるような構成図では、dup, swap, id しか使わない。dup, swap, idだけで構成された構成図をセットアップ〈setup〉の構成図と呼ぶことにする。
一方、構文解析木から作られる構成図は、演算子(+, ×, -)を導入していくので、演算子導入〈operator introduction〉の構成図と呼ぶことにする。
今までの考察から、整数式の構成図は、セットアップの構成図の後に、演算子導入の構成図(構文解析木)を繋げた形に出来ることが分かった。
yy + xx ------------[+] yy xx ----[×] ------[×] 演算子導入 y y x x 〜〜〜〜〜〜〜〜〜〜 -----[dup] -----[dup] セットアップ y x -------------[swap] x y
練習問題: セットアップと演算子導入
次のような入力列/出力列を持つような構成図を、セットアップの構成図の後に、演算子導入の構成図(構文解析木)を繋げた形で描け。描画方向は↑→とする。
- x |→| x + -x
- x, y, 2 |→| (x2 + 2(xy)) + y2
- a, b, c |→| (a + b) + c
- a, b, c |→| a + (b + c)
- c, b, a |→| ((a + b) + c)(a + (b + c))
- s, 2 |→| 2s2 + -(2s) + -2
- y, x |→| x + y, x + -y
- s, t, 2 |→| 2s2 + -(2s) + -2, 2t2 + -(2t) + -2
IXY記法
構成図のセットアップ部分では、dup, swap, id しか使わない。この3種の操作を1文字に短縮表記する。
- idを I と書く。
- swapを X と書く。
- dupを Y と書く。
これらの1文字は象形文字(意味はすぐ分かる)として使う。
テキスト記法において、例えば idid
dup は短く I
I
Y と書ける。さらに、
は省略可能として、IIY と書く。(swap
id);(id
swap);(id
id
dup) は、XI;IX;IIY と書けるが、';'の代わりに'
'を使うと:
- IIY
IX
XI
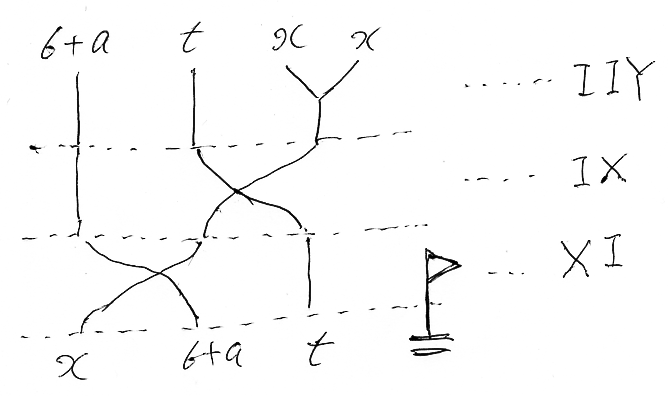
この書き方は次の図とマッチしている。この図は、x, 6 + a, x |→| 6 + a, t, x, x というセットアップを記述している。
練習問題: IXY記法
「練習問題: セットアップと演算子導入」で出来たセットアップ部を、IXY記法と''によりテキストで表現せよ。