単純式の操作の操作 (A5P4) - (保存用) 檜山正幸のキマイラ飼育記メモ編

※この記事は「記事5 問題集4」

ノード・ワイヤー図〈ストリング図〉の解説は：

ノード・ワイヤー図〈ストリング図〉

これより前に行うべき練習は：

今回は、式の操作を表す横棒記法の図やノード・ワイヤー図を、さらに操作する（変形する）。過去の定義や記法はチャラにしてるところもあるし、引き継いでいるところもある。

内容：

式の定義
式の操作
練習問題：操作の図示
練習問題：テキストによる表現からの図示
選択範囲〈セレクション〉
式の操作の操作とは
基本操作〈基本変形〉
例題
練習問題：ノード・ワイヤー図の変形

式の定義

ここで考える式は、次の構成素から組み立てられるものに限る。今までとはまた違った「式」の定義になる。

変数。変数の文字（名前）は何を使ってもよい（自由）。
掛け算記号 × 。
演算の優先順を示す括弧。丸括弧のみ。

次の注意事項がある。

掛け算の記号×は省略してよい。x×y は xy と書いてよい。
xyz を使ってもよい。xyz は、(xy)z の略記と考える。ただし、xyz = (xy)z と x(yz) は区別する（別な式とみなす）。
累乗の記法を使ってよい。yy は y² と書いてよい。y³ も使ってよい。y³ は、y²y = (yy)y の略記と考える。ただし、y³ = y²y と yy² は区別する（別な式とみなす）。

今まで出てきた式に比べて単純なので単純式〈simple expression | simple term〉とも呼ぶ。

式の操作

前節で定義した式（単純式）に対して、以下に述べるような操作を考える。操作の説明とともに、横棒記法も説明する。A, B などは式を表す文字（「メタ変数」と呼んだりする）。

掛け算（積） product

A, B が2つの式のとき、AとBを掛け算した式を作る操作を prod と書く。

例：操作の前（2つの式を横に並べている）

xy   yz^3

これらの式に対して、prod を行う。

例：操作の後

(xy)(yz^3)

これを、横棒記法を用いて、次のように書く。

  xy   yz^3
 ----------- prod
  (xy)(yz^3)

一般的には、

  A   B
 ------- prod
   AB

複製 duplication

Aが式のとき、同じAを2つにして横に並べる操作を dup と書く。

   A
 ------ dup
  A  A

入れ替え swap

A, B が2つの式のとき、AとBの並び順を入れ替える操作を swap と書く。

  A  B
 ------ swap
  B  A

何もしない identity

Aが式のとき、何もしないことを id と書く。

  A
 --- id
  A

練習問題：操作の図示

入力列／出力列は以前に定義したものとして、次のような入力列／出力列を持つような図（横棒記法の図、またはノード・ワイヤー図）を描け。

x |→| x³
x |→| x⁴ （x⁴ は、x²x² ではないことに注意）
x |→| x², x³, x⁴
a, b |→| (ab)²(ba)³
a, b, c |→| abc, a(bc)
概念や書き方に慣れるために、幾つか（必要なだけ）同様な作業を行え。

“横棒記法の図←→ノード・ワイヤー図の相互描き換え”、“描画方向の変更”なども以前の説明と同様、概念や書き方／描き方に慣れるまで、トレーニングとしての作業は自主的に行う。

練習問題：テキストによる表現からの図示

絵ではなく、文字（もちろん記号文字を含む）を普通に並べたものをテキストと呼ぶ。横棒記法の図、またはノード・ワイヤー図をテキストで表現する方法は既に述べた。以下に入力列とテキスト表現を示すので、それから図（横棒記法の図、またはノード・ワイヤー図）を描け。

入力列： a, b
テキスト表現： (dup $\otimes$ id);(id $\otimes$ dup $\otimes$ id);(prod $\otimes$ prod);prod
入力列： a, b
テキスト表現： ( (dup;(dup $\otimes$ id);(prod $\otimes$ id);prod) $\otimes$ id );prod
入力列： a, b
テキスト表現： (id $\otimes$ dup);(swap $\otimes$ id);(swap $\otimes$ id);(id $\otimes$ prod);prod
入力列： a, b
テキスト表現： (id $\otimes$ dup);(prod $\otimes$ id);prod
入力列： a, b
テキスト表現： (id $\otimes$ id);(id $\otimes$ dup);(swap $\otimes$ id);(id $\otimes$ swap);(swap $\otimes$ id);(id $\otimes$ prod)
入力列： a, b
テキスト表現： (id $\otimes$ dup);(swap $\otimes$ id);(id $\otimes$ swap);(id $\otimes$ prod)
入力列： a, b, c
テキスト表現： (swap $\otimes$ id);(swap $\otimes$ id);(id $\otimes$ prod)
入力列： a, b, c
テキスト表現： (prod $\otimes$ id);prod

[追記]

練習問題の3修正：

誤： (id $\otimes$ dup);(swap $\otimes$ id);(swap $\otimes$ id)(id $\otimes$ prod);prod
正： (id $\otimes$ dup);(swap $\otimes$ id);(swap $\otimes$ id);(id $\otimes$ prod);prod

[/追記]

やってみて分かるように、入力列が指定されなくても図（横棒記法の図、またはノード・ワイヤー図）を描ける。

選択範囲〈セレクション〉

図（横棒記法の図、またはノード・ワイヤー図）において、その一部分を「この部分」と指し示したいことがある。手描きの絵では、枠線で囲んで「この部分」を示せるが、テキストによる表現ではなかなかに困難。

苦肉の策で、二重鉤括弧を使うことにする。

次の図において、

   x
 ------ dup
  x  x         a    x
 ------ prod  --------- swap
   xx          x    a
 ------ id   --------- prod
   xx            xa
 --------------------- swap
  xa      xx
 ------------ prod
  (xa)(xx)

特定の部分を囲むために次のように書く。

『 x
 ------ dup
  x  x         a    x
 ------ prod  --------- swap
   xx          x    a
 ------ id   --------- prod
   xx      』    xa
 --------------------- swap
  xa      xx
 ------------ prod
  (xa)(xx)

この『』を使う書き方で指し示された図の一部分とは、

   x
 ------ dup
  x  x
 ------ prod
   xx
 ------ id
   xx

'『'が範囲四角形の左上、'』'が範囲四角形の右下を示す。指し示したい範囲が四角形でないときはうまくいかない。テキスト記法の限界だからしょうがない。ノード・ワイヤー図に対して、フリーハンドで枠線を描けるならば、自由な指定ができる。

二重鉤括弧で囲まれた部分を選択範囲〈セレクション | selection〉と呼ぶ。選択範囲を自由に指定するにはノード・ワイヤー図を使う。横棒記法の図では無理がある。

注意：項書換え系〈term rewriting system〉の用語では、選択範囲をリデックス〈redex〉と呼ぶ。無理に日本語にするなら、redex＝可簡約項＝可縮約項。

式の操作の操作とは

式（ここでは単純式）に対する操作過程は、横棒記法の図／ノード・ワイヤー図によって表現できる。その“式の操作”に対して“操作を加える”（変形する）ことを考える。操作対象が、横棒記法の図／ノード・ワイヤー図になる。

まず、基本操作（基本変形）を定義し、与えられた横棒記法の図／ノード・ワイヤー図の選択範囲に基本操作を施すことで“式の操作の操作”が定義される。

基本操作〈基本変形〉

A, B などは式（単純式）を表す。'-'の横棒は式への操作（swap, prodなど）を表す。'='の横棒は、“式の操作の操作”を表す。

レイアウト調整

図の変形として、交替律〈interchange law〉、エレベーター規則〈elevator rule〉などと呼ばれる変形法がある。「ノード／クラスタの位置を第一方向に沿ってズラしてもいい」という規則である。テキスト表現で書くなら：

(f $\otimes$ id_C);(id_B $\otimes$ g) と (id_A $\otimes$ g);(f $\otimes$ id_D) のあいだで相互変形してよい。

横棒記法の図なら：

   A
  ---f  C
   B   ---g
        D
 =============↓↑相互変形可能
        C
   A   ---g
  ---f  D
   B

キュリアの論説（Pierre-Louis Curien "The Joy of String Diagrams"）から、ノード・ワイヤー図〈ストリング図〉に関する説明を引用（絵だけ見れば十分）：

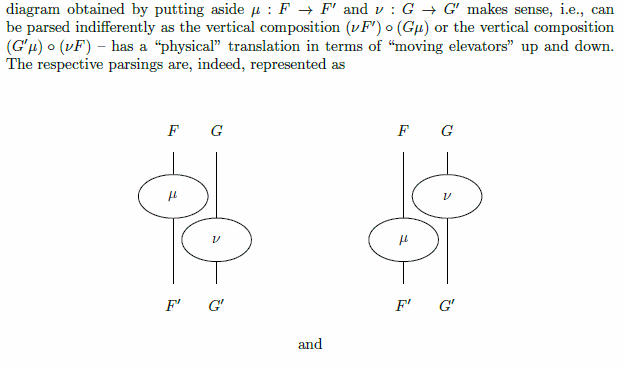
キュリアが使っている記号は：

   F
  ---μ  G
   F'   ---ν
         G'
 =============↓↑相互変形可能
         G
   F    ---ν
  ---μ  G'
   F'

手描き図や目視判断では、レイアウトの調整としてこの規則を無意識に使ってしまっていると思う。ので、あまり細かいことは言わず「レイアウト調整はしてよい」で済ませる。

idの削除 Remove Id

重要な注意：説明を横棒記法の図でしているが、ノード・ワイヤー図のほうがふさわしい。各自、ノード・ワイヤー図に描き換えて考えよ。ノード・ワイヤー図による書き方／描き方は、「例題」を参照せよ。

id操作を削除する。

     A
    ---- id
     A
 =========== RemoveId
     A

使用例：上記の基本操作を、選択範囲に対して適用する。

   a   x
  -------- prod
 『 ax
   ----- id
    ax     』
  ------- dup
  ax   ax
 =============== RemoveId
   a   x
  -------- prod
    ax
  ------- dup
  ax   ax

idの挿入 Insert Id

id操作を挿入する。idの削除と逆の操作になる。

     A
 =========== InsertId
     A
    ---- id
     A

ノード・ワイヤー図では、ワイヤーを引き伸ばすことで「idの挿入」を代替できる。

swapの繰り返しの削除 Remove Swap Swap

swapが連続して2回続くところを削除する。

   A  B
  ------ swap
   B  A
  ------ swap
   A  B
 ============= RemoveSwapSwap
   A  B

使用例：

    『  b   c
       ------- swap
        c   b
       ------- swap
  a   b      c』
  ----- prod ---id
    ab        c
 =================== RemoveSwapSwap
  a   b      c
  ----- prod ---id
    ab        c

注意：実際の計算では、swapの2回続きを挿入することがあるが、今回は扱わない。

dupの直後のswapを削除 Remove Swap

    A
  ------ dup
   A  A
  ------ swap
   A  A
 ============= RemoveSwap
    A
  ------ dup
   A  A

注意：実際の計算では、dupの直後のswapを挿入することがあるが、今回は扱わない。

3つのswapの配置を変える Change Crossing

双方向の変形なので、ChangeCrossing-1 と ChangeCrossing-2 がある。

横棒記法で表すのは辛いものがあるので、ノード・ワイヤー図に描き変えて理解せよ。

   A  B        C
  ----- swap  --- id
   B     A    C
  -- id -------- swap
   B    C      A
  ------- swap -- id
   C    B      A
 ====================== ChangeCrossing-1
   A       B  C
  --- id  ------ swap
   A    C      B
  ------- swap --- id
   C    A     B
  --id --------- swap
   C    B    A

   A       B  C
  --- id  ------ swap
   A    C      B
  ------- swap --- id
   C    A     B
  --id --------- swap
   C    B    A
 ====================== ChangeCrossing-2
   A  B        C
  ----- swap  --- id
   B     A    C
  -- id -------- swap
   B    C      A
  ------- swap -- id
   C    B      A

dupの位置を動かす Change Dup

双方向の変形なので、ChangeDup-1 と ChangeDup-2 がある。

      A
   -------- dup
   A      A
  --- dup --id
  A  A    A
 =============== ChangeDup-1
      A
   -------- dup
   A     A
  -- id ---- dup
  A    A   A

      A
   -------- dup
   A     A
  -- id ---- dup
  A    A   A
 =============== ChangeDup-2
      A
   -------- dup
   A      A
  --- dup --id
  A  A    A

prodの位置を動かす Change Prod

双方向の変形なので、ChangeProd-1 と ChangeProd-2 がある。

この変形を許すことは、掛け算の結合律を使えることと同じになる。

   A  B        C
  ------ prod --- id
    AB         C
   -------------- prod
      (AB)C
 ======================= ChangeProd-1
   A      B   C
  --- id ------- prod
   A      BC
  ------------ prod
     A(BC)

   A      B   C
  --- id ------- prod
   A      BC
  ------------ prod
     A(BC)
 ======================= ChangeProd-2
   A  B        C
  ------ prod --- id
    AB         C
   -------------- prod
      (AB)C

例題

次の2つのテキストで表現されるノード・ワイヤー図を考える。

(swap $\otimes$ id);(swap $\otimes$ dup);(id $\otimes$ id $\otimes$ swap);(id $\otimes$ prod $\otimes$ id);(id $\otimes$ prod)
id $\otimes$ ( (id $\otimes$ dup);(id $\otimes$ prod);prod )

1番のノード・ワイヤー図から2番のノード・ワイヤー図に至る変形（操作の操作）を記述してみる。横棒記法で描くのは無理があるので、ノード・ワイヤー図を手描きする。次のような描画法を使っている。

式の操作過程はノード・ワイヤー図で描く。
1. 描画方向は↓→。
2. ノードはドット（点、小さな黒丸、線の交点）。
3. ノードラベルもワイヤーラベルも省略。
“式の操作過程”の操作過程は横棒記法の図で描く。
1. 描画方向は↓→。
2. 横棒は、"-------"のような一本線（二重線ではない）。
選択範囲は赤枠で囲む。
選択範囲を変形した結果は青枠で囲む。

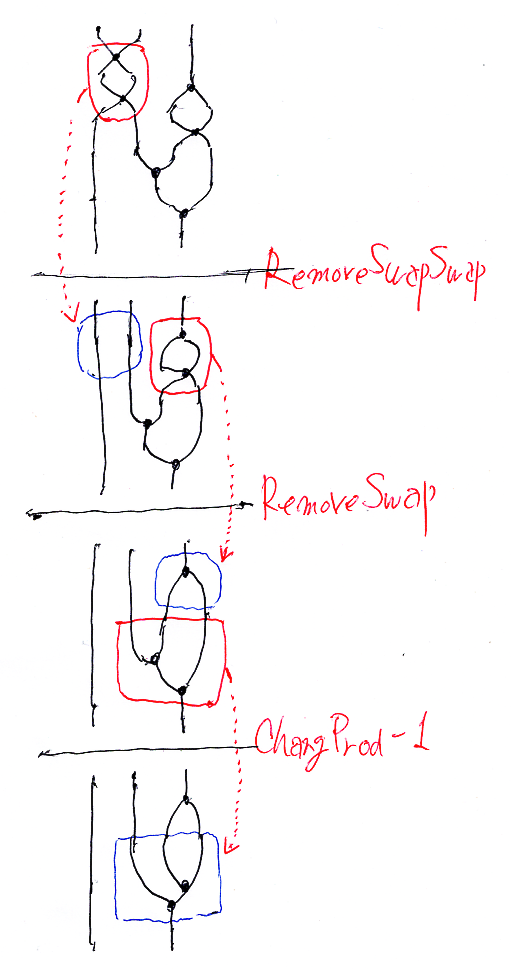
この変形過程を象形文字で書いてみる。

式の操作過程はテキスト（文字列）で書くが、象形文字を使う。
1. 描画方向は↓→。
2. id, dup, swap, prod を I, 人, X, Y と略記する（象形文字）。
3. ' $\otimes$ 'は省略して併置。あいだに空白を入れてもいい。
4. ';'の代わりに縦方向に並べる。
“式の操作過程”の操作過程は横棒記法の図で描く。
1. 描画方向は↓→。
2. 横棒は、"-------"のような一本線（二重線ではない）。
選択範囲には特に何の印もない。各自、目視で探して。

   X   I
   X  人
  I I  X
  I  Y  I
  I    Y
 ----------- RemoveSwapSwap
  I I   I
  I I  人
  I I  X
  I  Y  I
  I    Y
 ----------- RemoveSwap
  I I  I
  I I 人
  I I I I
  I  Y  I
  I    Y
 ----------- ChageProd-1
  I I  I
  I I 人
  I I I I
  I I  Y
  I   Y

余分なIを取り去れば：

  I I 人
  I I  Y
  I   Y

2次元的象形文字記法を1行のテキストに簡略化すると次のよう。2次元のレイアウト情報がなくなり、選択範囲も分からないので、解釈は極めて困難になる。

  XI;X人;IIX;IYI;IY
 ----------------------- RemoveSwapSwap
  III;II人;IIX;IYI;IY
 ----------------------- RemoveSwap
  III;II人;IIII;IYI;IY
 ----------------------- ChageProd-1
  III;II人;IIII;IIY;IY

一般的に使われている（メジャーな）記法は、組版印刷のコストなどの問題から、上記の“1行のテキスト”のような方式のことが多い。つまり、「記法が余りにも酷すぎる」のが実情。組版技術や出版コストという現実的な問題が、読者側に押し付けられて、負担を強いられる -- これが「分かりにくさ」の要因のひとつ。

レイアウト情報や選択範囲のような重要な情報が潰されてグチャグチャにされてしまった結果を、檜山は「シンボルスープ」とか「ハッシュドピクチャー」と揶揄している。例えば、上記の変形過程が、単なる等式の連鎖として書かれる可能性さえある -- ハッシュドピクチャーだ。



   (idprod)(idprodid)(ididswap)(swapdup)(swapid)

 =

   (idprod)(idprodid)(ididswap)(ididdup)(ididid)

 =

   (idprod)(idprodid)(idididid)(ididdup)(ididid)

 =

   (idprod)(ididprod)(idididid)(ididdup)(ididid)

練習問題：ノード・ワイヤー図の変形

次のそれぞれのケースで、例題にならって、1番のテキストに対応するノード・ワイヤー図から2番のテキストに対応するノード・ワイヤー図に至る変形（操作の操作）を記述せよ。

ケース1
1. (dup $\otimes$ id);(id $\otimes$ dup $\otimes$ id);(prod $\otimes$ prod);prod
2. ( (dup;(dup $\otimes$ id);(prod $\otimes$ id);prod) $\otimes$ id );prod
ケース2
1. (id $\otimes$ dup);(swap $\otimes$ id);(swap $\otimes$ id)(id $\otimes$ prod);prod
2. (id $\otimes$ dup);(prod $\otimes$ id);prod
ケース3
1. (id $\otimes$ id);(id $\otimes$ dup);(swap $\otimes$ id);(id $\otimes$ swap);(swap $\otimes$ id);(id $\otimes$ prod)
2. (id $\otimes$ dup);(swap $\otimes$ id);(id $\otimes$ swap);(id $\otimes$ prod)
ケース4
1. (swap $\otimes$ id);(swap $\otimes$ id);(id $\otimes$ prod);prod
2. (prod $\otimes$ id);prod

[追記]
ケース4を修正しました。

誤： (swap $\otimes$ id);(swap $\otimes$ id);(id $\otimes$ prod)
正：(swap $\otimes$ id);(swap $\otimes$ id);(id $\otimes$ prod);prod

ご指摘感謝＞ @koji8y さん。
[/追記]