問題集10の目的と解答と追加説明 (A19R10) - (保存用) 檜山正幸のキマイラ飼育記メモ編

※この記事は「記事19 解答10」

問題集10とは、次の記事（の問題部分）のことです：

スパイダーパズル (A17P10)

解答だけでなく、「どうしてこのような練習をするか？」や、関連する事項の説明もします。

内容：

スパイダーパズルと演繹システム
書き方の注意
与えられたプロファイルのスパイダーを構成する
構成不可能性定理 1
構成不可能性定理 2
構成可能性定理

スパイダーパズルと演繹システム

「スパイダーパズル (A17P10)」で次のように言いました。

この記事の問題をやれば、形式化された証明や演繹システムに対して、（詳細はともかくとして）かなりの程度のイメージが持てると思います。

スパイダーパズルは、人間がルールを決めて作ったパズル（ゲーム）です。演繹システムも、人間がルールを決めて作ったパズル（ゲーム）システムです。目的や複雑さが違うだけで、メカニズムは同じです。同列に論じてかまいません。

スパイダーパズルを実際に解いたり（プロファイルに対するスパイダーを構成したり）、スパイダーパズルのシステムとしての特性を証明したりすると、次のことが実感として分かるでしょう。

パズルのシステムは、人間が恣意的に作った人工的システムである。作り方の自由度が高く、色々なバリエーションがあり得る。
パズルのシステムを調べる際に、特別な予備知識は要らない。
パズルのシステムを調べる際に、特別に難しい議論をすることはない。
だが、長く煩雑な、ときに退屈な議論を続けることはある。技量も瞬発力も必要ないが、地味な持久力が要求される。

演繹システムに対しても、同じことが言えます。なぜなら、演繹システムも、人間がルールを決めて作ったパズル（ゲーム）システムだからです。

書き方の注意

次の書き方の約束は、あまり（ほとんどかも）使っていません。

メタ論理（形式されてない通常の論理）の論理記号は丸括弧で囲む。(∧), (⇒) など。
形式化された命題である論理式は引用符で囲む。"∀x∈R.∃y∈R.(y² = x)" のように。

形式化されている／されてないを特に強調したいときは、気まぐれに使います。

与えられたプロファイルのスパイダーを構成する

構成できる／できないを先に言うと：

B, A → A ○
B, A → B ×
B, A → C ○
A → A, B ×
B → A, B ○
C → A, B ×
C, C, B → A, A ○
B, B → A, A ○

構成可能なスパイダーにはその構成図を示します。構成図の最下段にテキスト表現も添えます。×印のプロファイルを持つスパイダーが構成できないことは、後で述べる構成不可能性定理から言えます。

※注意：二本棒横棒の区切りをハッキリさせる目的で'+'を入れているところがあります。が、いつでも入っているわけではありません。後で出てくる、上段にあるスパイダーの個数が未定の構成図のときは、'+'をうまく入れることが出来ません。

B, A → A

   ☆           ☆
 ====== Ent   ======== Ent
  B  A         A  B
 ----- swap   ------ a
  A  B          A
 ===========+=========== Comp
          B  A
         ------ swap
          A  B
          ---- a
           A
 swap;a

B, A → C

  ☆            ☆
 ===== Ent    ====== Ent
  B  A         A  B
 ----- swap   ----- c
  A  B          C
 ==========+========== Comp
         B  A
        ------ swap
         A  B
        ------ c
          C
 swap;c

B → A, B

   ☆           ☆
 ====== Ent  ======= Ent
   B          B  A
 ----- b     ------ swap
  B  A        A  B
 ===========+=========== Comp
            B
         ------ b
          B  A
         ------ swap
          A  B
 b;swap

C, C, B → A, A



   ☆         ☆

 ====== Ent  ====== Ent

   C           C

  --- d       --- d

   A           A              ☆

 =========+========== Prod ====== Ent

       C    C                B

      ---d ---d             ---- id

       A    A                B             別記

 ======================+=========== Prod  〜〜〜〜

                    C   C   B             A  A  B

                   --d --d --id          --------- F

                    A   A   B              A  A

                  ===================+=============== Comp

                    C   C   B

                   --d --d --id

                    A   A   B

                   ---------- F

                      A  A

 (ddid_B);F
別記部分
  ☆          ☆

 ===== Ent  ======= Ent

   A         A  B

  --- id     ----- a

   A           A

 ==========+============ Prod

        A      A  B

 F :=  --- id ------ a

        A       A
 F := id_Aa

B, B → A, A



    別記           別記

  〜〜〜〜〜    〜〜〜〜〜

     B              B

    --- F          --- F

     A              A

   ===========+=========== Prod

          B     B

         ---F ---F

          A    A

 FF
別記部分
    ☆          ☆

  ======= Ent ======= Ent

     B         B  A

   ----- b    ------ swap

   B  A        A  B

  =========+========= Comp

           B                     ☆

         ----- b             ========== Ent

          B  A                 A  B

         ----- swap           ------ a

          A  B                   A

        ================+================ Comp

                        B

                      ----- b

                       B  A

              F :=    ----- swap

                       A  B

                      ----- a

                         A

 F :=  b;swap;a

構成不可能性定理 1

目的とする命題（非形式的な、自然言語で書かれた命題）は次です。

形が Γ → B であるプロファイルに対して、スパイダーは構成できない。ただし、Γは、A, B, C からなるリストで、B（単一のB）ではない。

スパイダー構成図を「上から見ていく方法」と「下から見ていく方法」の二種で証明してみます。この二種は、実質は同じことです。共通に使う補題があるので、それを先に示します。

共通の補題

スパイダー〈ノード・ワイヤー図 | ストリング図〉Fに関する次の条件を考える。

[条件ア] スパイダーFのプロファイルが Γ → B であり、ΓはBではない。

スパイダー F, G, H に関する次の構成図（のワンステップ）を考える。

  F   G
 ===+=== Comp
    H

このとき、次が成立する。

[補題] Hが条件アを満たすなら、FかGの少なくとも一方は条件アを満たす。

対偶をとれば、

[補題の対偶] FとGのどちらも条件アを満たさないなら、Hも条件アを満たさない。

では、補題を示す。Hは条件アを満たすとして、スパイダーにプロファイルを添えた構成図を描く。

  F:Γ→Δ   G:Δ→B
 ==========+========== Comp
        H:Γ→B

Δの形により場合分けして：

Δ = B 、つまり Gのプロファイルは B → B 。
Δ = B ではない。

場合1なら、F:Γ→B が条件アを満たす。場合2なら、G：Δ→B が条件アを満たす。オワリ。

上から見ていく方法

補題で出した条件アは引き続き参照する。

スパイダー構成図の最上段は☆である。☆に対して使用できる操作は次のいずれかである。

id, dup, swap を具体化してのEnt
a, b, c, d のEnt

それぞれの場合について：

id_B のプロファイルは B → B だが、この形は条件から除外されているので、「id, dup, swap のEnt」からは、条件アを満たすスパイダーは得られない。
「a, b, c, d のEnt」からも、条件アを満たすスパイダーは得られない。

最上段以外で登場する操作は次のいずれかである。

Prod
Comp

それぞれの場合について：

Prodにより得られたスパイダーのプロファイルの右辺リストは、長さ2以上となるので、上段が何であれ、条件アを満たすスパイダーは得られない。
補題の対偶より、Comp構成の上段のどちらも条件アを満たさないなら下段も条件アを満たさない。

以上より、どのようなスパイダー構成図でも、条件アを満たすスパイダーは出現しない。よって、条件アを満たすスパイダーは構成できない。オワリ。

下から見ていく方法

条件アを満たすスパイダーが結果（最下段）となるスパイダー構成図が存在すると仮定する（背理法の仮定）。結果を得るために使用した操作は次のいずれかである。

id, dup, swap を具体化してのEnt
a, b, c, d のEnt
Prod
Comp

それぞれの場合について（詳細は「上から見ていく方法」）：

条件アを満たすスパイダーは得られない。
条件アを満たすスパイダーは得られない。
条件アを満たすスパイダーは得られない。

したがって、結果（最下段の条件アを満たすスパイダー）は、Compによって作られる。補題より、上段左か、上段右は条件アを満たすスパイダーである。

今、上段から条件アを満たすスパイダーを選ぶ。同じ考察により、その上段から、条件アを満たすスパイダーを選ぶ。この選択は無限に行えるので、構成図は無限の高さ（上下方向のサイズ）を持つことになる。

しかし、実際は構成図は有限の高さだから、条件アを満たすスパイダーが結果となるスパイダー構成図は実は存在しない。よって、条件アを満たすスパイダーは構成できない。オワリ。

構成不可能性定理 2

目的とする命題（非形式的な、自然言語で書かれた命題）は次です。

プロファイルの形が Γ → Δ で、リストΓ内にBが出現せず、リストΔ内にBが出現するとき、このプロファイルに対してスパイダーは構成できない。

スパイダー〈ノード・ワイヤー図 | ストリング図〉Fに関する次の条件を考えます。

[条件イ] スパイダーFのプロファイルが Γ → Δ であり、リストΓ内にBが出現せず、リストΔ内にBが出現する。

条件イの否定を条件ウとします。

[条件ウ] スパイダーFのプロファイルが Γ → Δ であり、リストΔ内にBが出現するなら、リストΓ内にもBが出現する。

条件ウが条件イの否定であることがピンとこない人は、すぐ下の補足を参照してください。

[補足]

リストΓ内にBが出現することを、"B occurs in Γ" から bocc(Γ) と書くことにします。また、論理記号 (∧), (∨), (⇒), (¬) を使います。これは、記述を短縮する目的だけで、形式化した演繹システム内で考えるわけではありません。あくまで、非形式的な通常証明のなかで、短縮した記号的表現を使うだけです。別な言い方をすると；これを書いている檜山は、現実世界の人間どうしのコミュニケーションを目的として書いています。

条件イの主張は、

(¬)bocc(Γ) (∧) bocc(Δ)

これを否定すると、

(¬)( (¬)bocc(Γ) (∧) bocc(Δ) )

通常我々が現実世界で使っているド・モルガンの法則から、

bocc(Γ) (∨) (¬)bocc(Δ)

(∨)の左右を入れ替えてもいいから、

(¬)bocc(Δ) (∨) bocc(Γ)

通常我々が現実世界で使っている古典論理では、これは含意を意味するので、

bocc(Δ) (⇒) bocc(Γ)

つまり、

リストΔ内にBが出現するなら、リストΓ内にもBが出現する。

[/補足]

任意のスパイダー構成図が次の性質を持つことを示すことにします。

[性質エ] スパイダー構成図に出現するすべてのスパイダーは、条件ウを満たす。

スパイダー構成図に関する“構造帰納法”を用いて証明します。準備として、結果（最下段）をひとつ持つスパイダー構成図を場合分けします。

スパイダー構成図がノード（構成ステップ）をひとつしか持たず、それが「id, dup, swap を具体化してのEnt」の場合
スパイダー構成図がノード（構成ステップ）をひとつしか持たず、それが「a, b, c, d のEnt」の場合
スパイダー構成図の最後のノード（構成ステップ）がProdの場合
スパイダー構成図の最後のノード（構成ステップ）がCompの場合

場合1

さらに、id, dup, swap で場合分けする。X, Yは、A, B, C のどれかを表す。

      ☆
    ======= Ent
       X
F =   --- id
       X

このとき、下段のスパイダーFに関して、

出力列にBが出現する (⇒) 入力列にBが出現する

なので、条件ウを満たす。

       ☆
    ========= Ent
       X
F =  ----- dup
      X  X

このとき、下段のスパイダーFに関して、

出力列にBが出現する (⇒) 入力列にBが出現する

なので、条件ウを満たす。

        ☆
    =========== Ent
       X  Y
F =   ------ swap
       Y  X

このとき、下段のスパイダーFに関して、

出力列にBが出現する (⇒) 入力列にBが出現する

なので、条件ウを満たす。

場合2

さらに、a, b, c, d で場合分けする。

       ☆
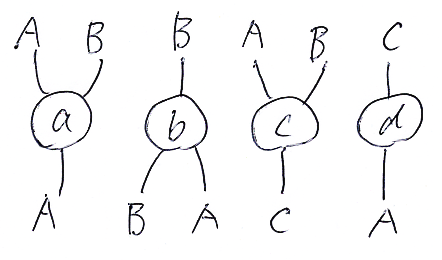
    ========== Ent
      A  B
F =  ------ a
       A

このとき、下段のスパイダーFに関して、出力列にBは出現しないので、

出力列にBが出現する (⇒) 入力列にBが出現する

は成立して、条件ウを満たす。

       ☆
    ========== Ent
       B
F =  ------ b
      B  A

このとき、下段のスパイダーFに関して、

出力列にBが出現する (⇒) 入力列にBが出現する

なので、条件ウを満たす。

       ☆
    ========== Ent
      A  B
F =  ------ c
       C

このとき、下段のスパイダーFに関して、出力列にBは出現しないので、

出力列にBが出現する (⇒) 入力列にBが出現する

は成立して、条件ウを満たす。

       ☆
    ========== Ent
       C
F =  ----- d
       A

このとき、下段のスパイダーFに関して、出力列にBは出現しないので、

出力列にBが出現する (⇒) 入力列にBが出現する

は成立して、条件ウを満たす。

場合3

スパイダー構成図の最後のノード（構成ステップ）がProdなので、



   F:Γ→Δ   G:Σ→Π

  ==========+========== Prod 最後のノード

    FG:Γ Σ → Δ Π

下段の出力列にBが出現するには、

ΔにBが出現する
ΠにBが出現する

の少なくとも一方が成立している。

上段のF, Gが条件ウを満たすなら、

ΓにBが出現する
ΣにBが出現する

の少なくとも一方が成立している。

これらより、下段の入力列 Γ Σ にBが出現するから、スパイダー F $\otimes$ G は次（条件ウ）を満たす。

出力列にBが出現する (⇒) 入力列にBが出現する

Prod構成ノードにおいて、

上段のスパイダーが条件ウを満たすなら、下段のスパイダーも条件ウを満たす。

場合4

スパイダー構成図の最後のノード（構成ステップ）がCompなので、



   F:Γ→Δ   G:Δ→Σ

  ==========+========== Comp 最後のノード

      F;G:Γ → Σ

下段の出力列にBが出現するには、

ΣにBが出現する

上段のGが条件ウを満たすなら、

ΔにBが出現する

上段のFが条件ウを満たすなら、

ΓにBが出現する

これらより、下段の入力列ΓにBが出現する。つまり、スパイダー F;G は次（条件ウ）を満たす。

出力列にBが出現する (⇒) 入力列にBが出現する

Comp構成ノードにおいて、

上段のスパイダーが条件ウを満たすなら、下段のスパイダーも条件ウを満たす。

総括

任意のスパイダー構成図が与えられたとき、場合1と場合2の考察から、☆の直下のスパイダーは条件ウを満たす。場合3と場合4の考察から、上段が条件ウを満たすなら、下段もまた条件ウを満たす。したがって、スパイダー構成図に出現するすべてのスパイダーは条件ウを満たす。言い方を換えると、任意のスパイダー構成図は性質エを満たす。

[性質エ] スパイダー構成図に出現するすべてのスパイダーは、条件ウを満たす。

特に、結果（最下段）のスパイダーも条件ウを満たす。よって、条件ウを満たさないスパイダー（条件イを満たすスパイダー）を構成することは出来ない。

構成可能性定理

目的とする命題（非形式的な、自然言語で書かれた命題）は次です。

プロファイルの形が B → Δ で、ΔはAとCから構成されるリスト（非空でBは含まないリスト）のとき、このプロファイルに対してスパイダーは構成できる。

幾つかの準備が必要です。まず、この節で使う F, G は特定のスパイダーを表す固有名詞です。

         B
       ------ b
        B  A
 F :=  ------ swap
        A  B
       ------ a
         A


         B
       ------ b
        B  A
 G :=  ------ swap
        A  B
       ------ c
          C

F:B→A, G:B→C で、FもGも構成可能です（構成図は各自描いてみてください）。

次に、整数 2, 3, 4, ... で番号付けられたスパイダー達 H_n を定義します。

H₂ := dup_B : B → B, B
H_n+1 := dup_B;(id_B $\otimes$ H_n) : B → B, B, ..., B （右辺は(n +1)個のB）

H₂は明らかに構成可能で、H_nが構成可能ならH_n+1が構成可能なのは、次の構成図から分かります。



   ☆            別記部分

 ======= Ent    〜〜〜〜〜〜〜〜〜〜〜〜〜

    B             B  B

  ----- dup      --------------- id_BH_n

   B  B           B, B, ..., B （(n+1)個）

 ============+================================== Comp

    dup_B;(id_BH_n): B → B, B, ..., B （(n+1)個）
別記部分
  ☆          H_n の構成図

 ===== Ent  〜〜〜〜〜〜〜〜〜〜〜〜〜

   B              B

  --- id     --------------- H_n

   B          B, ..., B （n個）

 ========+=========================== Prod

   id_BH_n : B, B → B, B, ..., B （(n +1)個）

また、n個のスパイダー（n ≧ 2）から1個のスパイダーを構成する操作（構成法）として、Prod_nを定義しましょう。K₁, ..., K_n が任意のn個のスパイダーだとして、



  K₁ ・・・ K_n

 ============== Prod_n

  K₁...K_n

Prod_nからProd_n+1を構成するには、



  K₁ ・・・ K_n

 ============== Prod_n

  K₁...K_n  K_n+1

 ================== Prod

 (K₁...K_n)K_n+1

Prod₃, Prod₄ などが構成図内に出現したら、それは長い構成図の略記と思えばいいのです。（構文的マクロ展開をご存知に方は、マクロ展開だと理解してください。）構成図にProd_nが出現しても、それを長い構成図に置き換えて消去することが出来るので、Prod_nを使用しても使用しなくても、スパイダーの構成可能性に影響はありません。

ΔがAとCから構成される長さnのリストだとして、B→Δ をプロファイルに持つスパイダーの構成法を以下に述べます。

n個のスパイダー K₁, ..., K_n を次のように定義する。

リストΔのi番目の項目がAのとき、K_i = F とする。
リストΔのi番目の項目がCのとき、K_i = G とする。

K_iはFかGのどちらかで、FもGも構成可能なので、次のような構成図を作れる。



   ここにナニヤラカニヤラ

   〜〜〜〜〜〜〜

    K₁ ・・・ K_n

H_nも構成可能だったので、Prod_nを使って次の構成図を作れる。



           〜〜〜〜〜〜〜

           K₁ ・・・ K_n

 〜〜     =============== Prod_n

  H_n        K₁...K_n

 ======================= Comp

    H_n;(K₁...K_n)

H_n:B → B, ..., B（n個）、 (K₁ $\otimes$ ... $\otimes$ K_n):B, ..., B（n個） → Δ なので、これらを結合したスパイダーのプロファイルは B → Δ となる。オワリ。