モノドロミーグラフとか
えーと、最初に言っておくが; 複素解析ともリーマン面とも微分方程式とも特異点とも接続とも曲率とも、何の関係もない。被覆とは少し似ているし、(正錐により順序が付いた可換群としての)整係数ホモロジー群ともなんとなく関係ありそう。だが、、再帰的定義と引数渡しとオートマトンの問題。実装予定あり。
螺旋階段の話に近いかな。螺旋階段の写真は先のエントリーで出したからもういいや。本編の関連エントリーは、コレとかコレとか。
有向グラフGがあって、Gから圏Vへのグラフ準同型(関手から圏演算に関する事を除いた対応)Fがあるとする。Gから作られた自由圏(道の圏)を D = Path(G) とすると、Fは自然に圏Dから圏Vへの関手に拡張できる。よって、Fは関手と考えても別に差し支えない。
tがグラフGの頂点、Cはtを通るGの素サイクルだとする。Cに含まれる辺を c1, c2, ..., cn とする。ただし、c1の始点はt、cnの終点もt。F(C) を、F(c1);F(c2); ...;F(cn) in V の意味だとする。Cはサイクルだから、F(C):F(t)→F(t) in V、つまり、F(C)は End(F(t)) in V に入る。
書くのが楽になるように、m = F(C)、M = End(F(t)) と置く。Mはモノイドで、m∈M となる。Fの存在を前提にすれば、mはCから決まる。mをサイクルCの(Fに関する)モノドロミー元とかモノドロミー射と呼ぶことにする。mはモノイドM(=End(F(t)) in V)の元(要素)だし、圏Vの射になっている。
モノドロミー(monodromy)の語源は、run round なので、グルッと一周したときの量に形容詞として「モノドロミー」を付けるのは許されるでしょ。似た(?)用語でホロノミー(holonomy)もあるけど、モノドロミーが先に思いついたのでモノドロミーを使う。
まーともかく、グラフGのノードtと、tを基点と考えたサイクルCからモノドロミー元mが決まる。モノイドMにおけるmのベキ(累乗)を普通のとおり、m0, m1, m2 のように書く。集合 {mk | k = 0, 1, 2, ...} を、tとCから決まるモノドロミーモノイドと呼ぶことにする。モノドロミーモノイドは、モノイドM(= F(C) in V)の部分モノイドで、モノドロミー元mから単元生成されたモノイドとなる。
モノドロミーモノイドが無限集合になると、無限の螺旋階段になるので困る。有限の場合を扱う。モノドロミーモノイドが有限とは、生成元であるモノドロミー元mに、mn+1 = mp(0≦p≦n)という関係が成立すること。
有限なモノドロミーモノイドの例をいくつか示す。
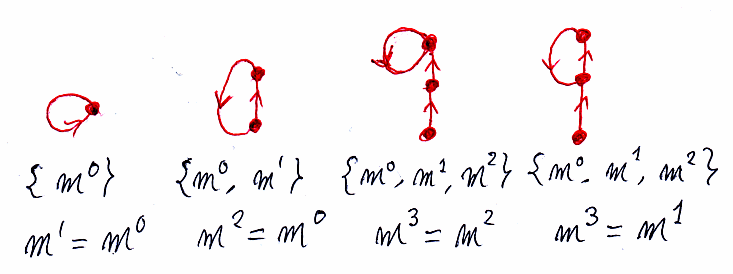
この絵は、モノドロミーモノイドのケイリーグラフとなっている。ケイリーグラフ(Cayley graph)は群と生成団に対して定義されるが、モノイドと生成団に対しても同様に定義できる。モノドロミーモノイドのケイリーグラフだから、モノドロミーグラフとしよう。
モノドロミーモノイドが有限なら、基点tとサイクルCから作られる螺旋階段は無限には昇らずに適当な所で循環する。循環の様子は、モノドロミーモノイドの循環と同様となり、それは、モノドロミー元mのベキ(累乗)の性質から決まる。絵に描くと次のよう。
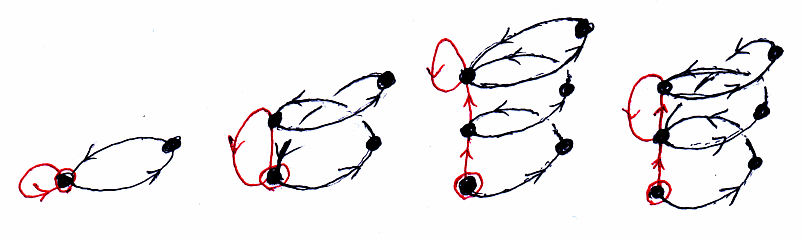
上の絵のような有限循環する螺旋階段で記述される参照グラフや接ぎ木手順は次のようだ。
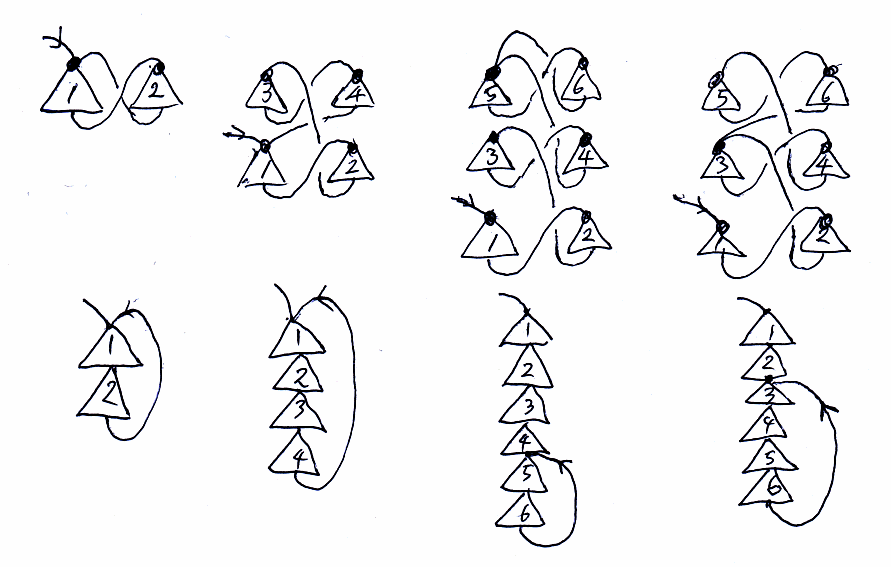
参照グラフと接ぎ木に関しては先のエントリーで述べた。