圏FinRelが面白い

FdHilbとRelが似てることは、ボブ・クックが「物理系実務者…」のなかで指摘している。と、自分で書いているよ(苦笑)。実際、クック論文「4.Quantum?」のところ（P.4からP.6）に記述がある。

特に、対象を有限集合だけに制限したRel＝FinRelは手で簡単に触れる。むずかしいことはやっぱり分からんから、こういう簡単な例をいじることにしよう。で、絵を描いた。絵の下に、思い付きをゴタゴタダラダラ書く。

---

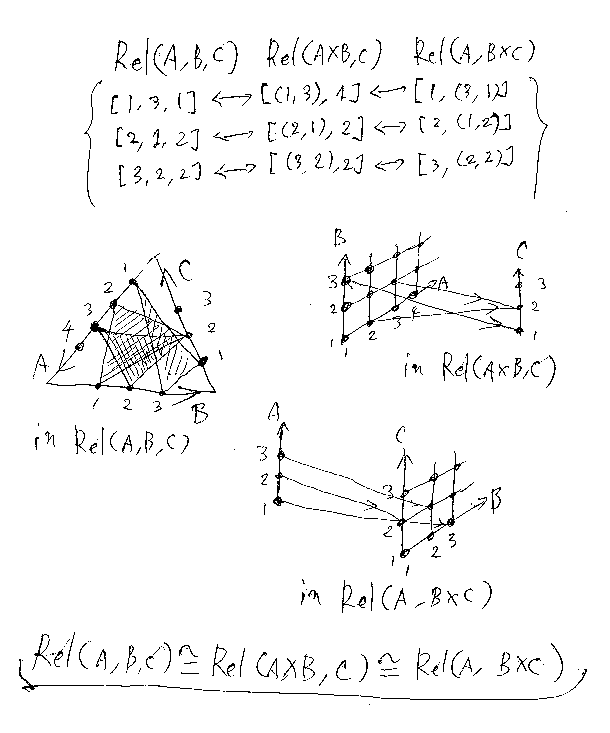
まず、直積をモノイド積としてRel（もちろんFinRelも）はコンパクト閉圏なのだが、A^* = A というところが特徴的。双対化スターが恒等に退化している。この状況は、内積があれば双対空間が要らなくなるのと似てる。

随伴は、Rel(A×B, C) ≒ Rel(A, B×C)で与えられる。(-)×X の随伴が X×(-) となる。積（掛け算関手）と指数（ベキ関手）が一致してしまう。という状況を効果的に描くために考えたこと；（以下）

圏論とはまったく離れて、古典的／集合ベースの関係を考える。単項、二項、三項の関係の全体を Rel(A), Rel(A, B), Rel(A, B, C)のように書く。r∈Rel(A, B, C) ⇔ r⊆A×B×C のように考える。rの要素を関係要素と呼ぶことにする。

便宜上、無項関係 Rle() = {0} と約束する。無項関係が１つだけ存在することに注意。定義から、Rel(A) = Pow(A) となる。また、Pow(A) = Rel(A, 1) = Rel(1, A)なども（同型の意味で）成立する。

上の絵で言いたいことは、関係要素がどう図示されるか。まず、r∈Rel(A, B, C)なら、rに含まれる関係要素(a, b, c)はA×B×Cの点となる。が、二項関係を二部グラフで描くことにすると、A×B→C、A→B×C の辺となる。さらに、直和 A + B + C の上で関係要素を表現すると三角形になる。まとめると：

外の空間	関係要素
A×B×C	点（0-単体）
A×B + C	辺（1-単体）
A + B + C	三角形（2-単体）

これから、次の3者が対応する。

1. A×B×C 内の点の集まり＝部分集合
2. A×B + C 内の辺の集まり＝二部グラフ
3. A + B + C 内の三角形群

他にも面白いことがあるが別エントリーにする。