メイト定理

メイト〈mate〉に関してnLab項目 https://ncatlab.org/nlab/show/mate を毎回参照するのだが、分かりにくいペースティング図を解釈して、毎回忘れる。ここに、ストリング図を描いておく。

状況設定は、

• Title: Multivariable adjunctions and mates (2012)
• Authors: Eugenia Cheng, Nick Gurski, Emily Riehl
• Pages: 52p
• URL: https://arxiv.org/abs/1208.4520

次のような絵になる。（下に説明）

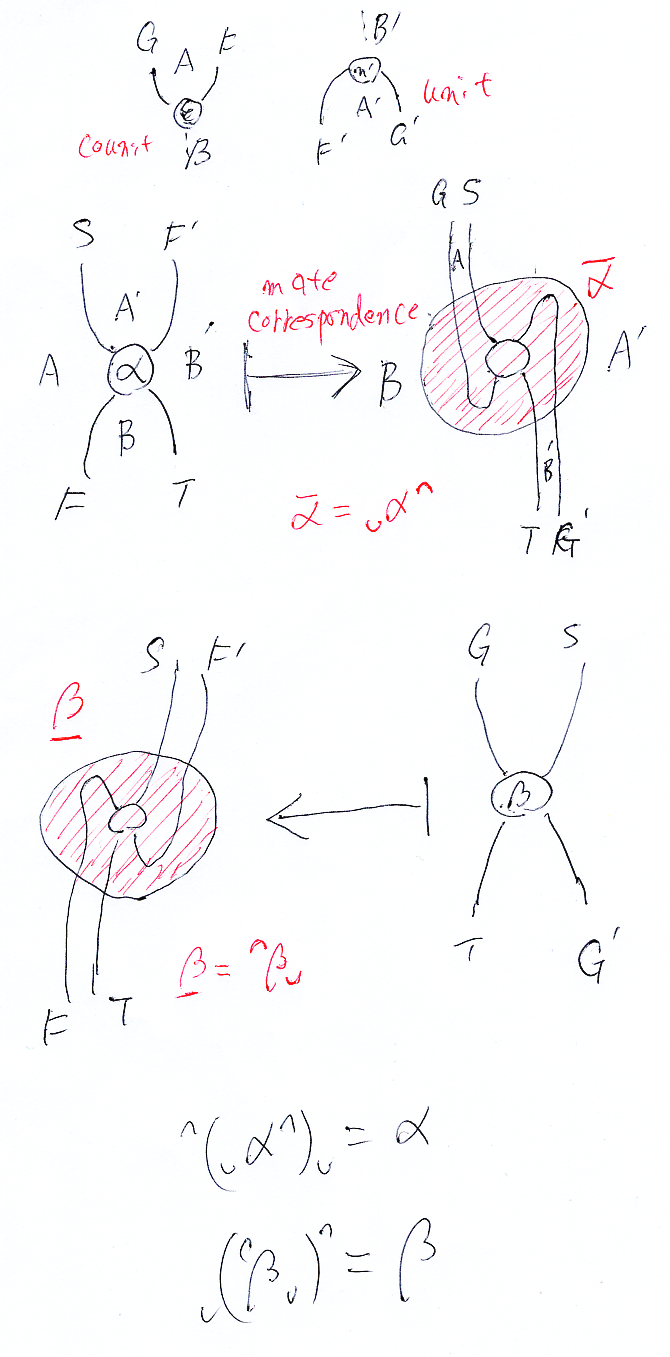
随伴系が2つある。

• (ε, η): F -| G :B→A
• (ε', η'): F' -| G' :B'→A'

この状況で、

• Nat(S*F', F*T:A→B') Nat(G*S, T*G':B→A')

という自然変換集合の同型がある。これをメイト対応〈mate {correspondence | bijection | isomorphism}〉と呼ぶ。メイト対応で対応する2つの自然変換は、互いにメイトであるという。どっちが左とか右はないようだ。

メイト対応の向きも特に“決め”がない。今回の設定では、

• 左から右： _∪(-)^∩
• 右から左： ^∩(-)_∪

２つある随伴を自明な随伴系 C^ -| C^ :C→C にしたり、図で左側の圏を自明圏にしたりすると、メイト定理の特殊形が得られる。モノイド圏における射の双対（左右の別がある）、単一の随伴系のホムセット同型などが特殊な形の例。

また、単一の随伴系の持ち上げ定理もメイト対応から得られる。

引用した論文では、多変数随伴のメイト定理を示している。

[追記]
メイト対応の片方を ∪／∩または∪-∩とすると、もう一方は∩＼∪または∩-∪と書ける。

• ∩(∪-∩)∪ = (-)
• ∪(∩-∪)∩ = (-)

メイトと同義語で

• 随伴（adjunct）
• 共役（conjugate）
• 転置（transpose）
• 双対（dual）

使い分けはまったく曖昧。どうにもならない。

とりあえず、転置オペレーター／反転置オペレーターを使っている。ただし、方向と名前を決める基準が何もない。特にメイトになるとどうしようもない。お手上げだ
[/追記]