ノード・ワイヤー図〈ストリング図〉 (A1) - (保存用) 檜山正幸のキマイラ飼育記メモ編

※この記事は「記事1」

ノード・ワイヤー図はいたるところで使う、極めて重要なツールである。

内容：

ノード・ワイヤー図とは
描画方向
結合と併置
テキスト記法
グルーピング〈ブラケティング〉と描き換え
横棒記法
ノードの形状
図の引用元

ノード・ワイヤー図とは

ノード・ワイヤー図〈nodes-and-wires diagram〉は、有向グラフ〈directed graph〉とほぼ同じだが、描画法と解釈において、有向グラフと次の点が異なる。

有向辺であるワイヤーは、単なる線として描き、矢印は通常は書かない（書いてもいいが）。その代わり、描くキャンバス側に方向を決めておく。
ワイヤー（有向辺）で結ばれていないノードであっても、位置関係が意味を持つ。

また：

ノード、ワイヤーに付く名前、値、記号、注釈などは、それぞれノードラベル、ワイヤーラベルと呼ぶ。ラベルが膨大な情報を持つこともある。
ラベルの代わりに、色・形状を使ってノード／ワイヤーに情報を付加することがある。

ワイヤーをストリング〈string〉と呼ぶことがあり、ノード・ワイヤー図をストリング図〈string diagram〉とも呼ぶ。

描画方向

キャンバス（図を描く場所・広がり）は2次元で、第一方向〈主方向〉と第二方向〈副方向〉がある。方向のペアを「←↓」のような書き方で示す。これの意味は、

第一方向は右から左、第ニ方向は上から下

“旗”で示すこともある（旗は檜山のプライベート・ローカル利用）。

この旗の意味は、

第一方向は下から上、第二方向は左から右（↑→と同じ）

↑→で描かれた図の例（ストリート論文から引用）：

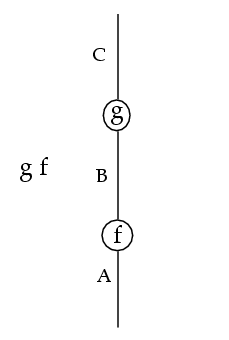
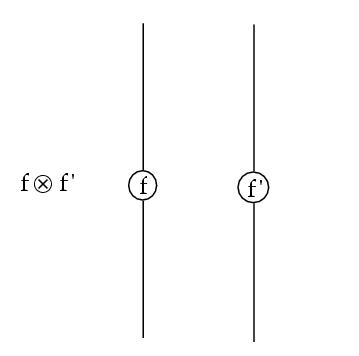
→↓で描かれた図の例（ガーナー／シュルマン論文から引用）：

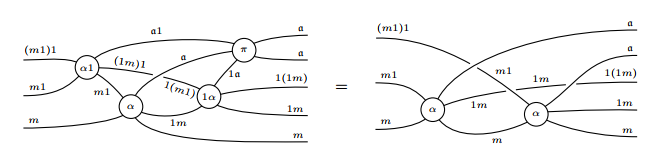
結合と併置

ワイヤーの矢印は描かない（ことが多い）が、キャンバスの描画方向から矢印は決まる。「(f)→(g)」は、「ノードfとノードgが、この順でワイヤーで結ばれている」ことだとする。

ワイヤーは第一方向に描く。多少斜めになってもよいが、第二方向に描いてはいけない。
(f)→(g) であるとき、2つのノードfとgはこの順で結合されている〈composed〉という。
2つのノードが、第二方向に関して位置が揃っているとき、2つのノードはこの順で併置されている〈juxtaposed〉という。

例（ストリート論文から引用）：

次図は、描画方向↑→で、fとgはこの順で結合されている。なぜなら、ワイヤーで結ばれているから。

次図は、描画方向↑→で、fとf'はこの順で併置されている。なぜなら、横（第二方向）に揃っているから。

テキスト記法

実際に絵を描くのは手間だし、現状では伝達も難しい（手描き絵をスキャンして画像データ化等）ので、テキストで表現する。

ノードfとgが、この順で結合されているとき、f;g または g $\circ$ f と書く。
ノードfとgが、この順で併置されているとき、f $\otimes$ g と書く。
「;」「 $\circ$ 」「 $\otimes$ 」以外の記号を使うときもある。「*」「・」「 $\oplus$ 」「×」など。使う記号は好みの問題なので、気にしてもしょうがない。
結合または併置の記号を省略することもよくあるが、混乱するので我々は省略しない。前節のストリート〈Ross Street〉の例では、「 $\circ$ 」が省略されている。
ワイヤーAを、ノードとみなしたい（あたかもノードであるように扱いたい）ときは、id_A または 1_A と書く。

描画方向↑→の場合の説明（クック論文から引用）：

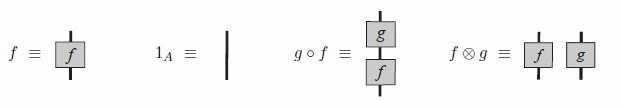
グルーピング〈ブラケティング〉と描き換え

ノード・ワイヤー図の複数のノード群を、まとめてひとつのノードのように考えたいことがしばしばある。ノード群をまとめることをグルーピング〈grouping〉またはブラケティング〈bracketing〉という。グルーピングは、テキストで考えると括弧付けになるので、「ブラケット」という言葉が使われている。

グルーピングを実際に描画するには、枠線で囲むが、ほとんどの場合、心の中でグルーピングして描画はしない。グルーピングされたそれぞれのカタマリを「群」と呼ぶのはまずい（群論の「群」とかぶる）ので、クラスタ〈cluster〉と呼ぶ。グルーピングをクラスタリング〈clustering〉と呼んでもいいが、コンピュータ屋さんは別な意味で「クラスタリング」を使う。定着した用語がなく、クラスタ以外に、ゾーン〈zone〉、チェンバー〈chamber〉、ピース〈piece〉などともいう。

以下の図は、(f;g) $\otimes$ u を、様々な描画方向で描いたものだが、グルーピング〈ブラケティング〉も色々ある（図の後）。

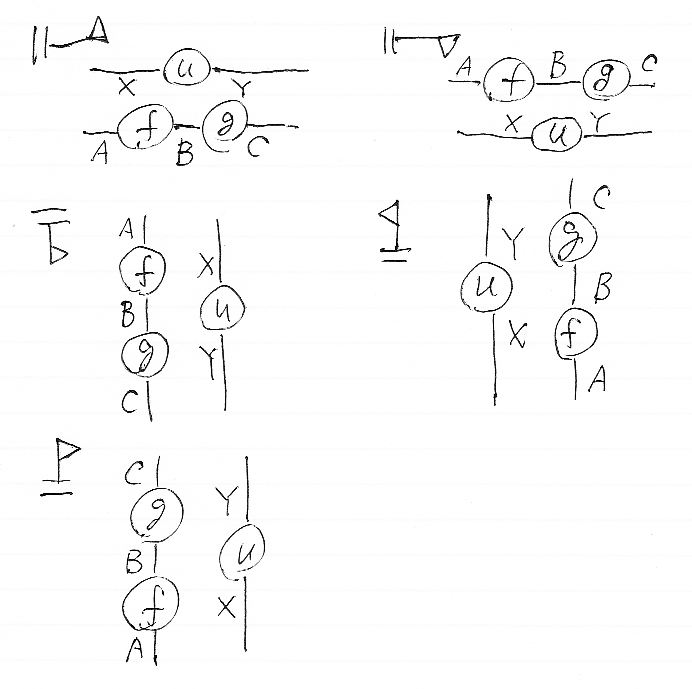
(f;g) $\otimes$ u
( (f $\otimes$ id_X);(id_B $\otimes$ u) );(g $\otimes$ id_Y)
(f $\otimes$ id_X);( (id_B $\otimes$ u);(g $\otimes$ id_Y) );
( (f $\otimes$ ;id_B) $\otimes$ (id_X;u) );(g $\otimes$ id_Y)
(f $\otimes$ id_X);( (id_B;g) $\otimes$ (u;id_Y) )

様々なグルーピングをいちいち区別して扱うのは煩雑なので、演算としての「;」「 $\otimes$ 」に結合律と単位律が成立するとして、異なるグルーピングを同一視する。同一視できる範囲内での図の描き換え（レイアウト変更）は自由に行ってよい。ただし、描き換え自体を議論するときは話が別で、どんな描き換えをしたかを意識することになる。

横棒記法

図とテキスト記法の中間的な記法として横棒記法〈horizontal-bar notation〉がある。

図のノードを横棒で書く。
ノードラベルは、横棒の左側または右側に添える。
ワイヤーラベル（ワイヤーに関する情報）は、横棒と横棒のあいだに書く。
横棒と横棒のあいだは段〈berth | layer〉と呼ぶ。ただし、最上段の上に横棒はなく、最下段の下にも横棒はない。
段は、単一のワイヤー、または併置された複数のワイヤーを表す
横棒をテキストで書くには、'-'を並べる。'='を使う場合もある。
全体を上から下へと読むが、下から上に向かう場合もたまにある。つまり、描画方向は↓→か↑→。

例：

以前の例の f, g, uをそれぞれ横棒記法で書く。

  A      B      X
 ---f   ---g   ---u
  B      C      Y

(f;g) $\otimes$ u を横棒記法で書く。

  A
 ---f  X
  B   ---u
 ---g  Y
  C

fとuを揃えて（併置として）書く。

  A    X
 ---f ---u
  B    Y
 ---g
  C

省略されている（と考える）id_Yも書く。

  A    X
 ---f ---u
  B    Y
 ---g ---id
  C    Y

id_Xを書く。

  A    X
 ---f ---id
  B    X
 ---g ---u
  C    Y

id_Xを省略する。

  A
 ---f
  B    X
 ---g ---u
  C    Y

例は多くないが、ノードを段、ワイヤーを横棒に対応させたほうが便利なこともある。この書き方がオフィシャルに使われることはまずないが、プライベートになら使ってもよい。

 ---A
  f
 ---B

この場合、最上段と最下段は空白（何もない）になる。次のような場合は、デフォルトの最上段（aの上の段）が省略されている。

  a
 ---A
  f
 ---B

同様に、次のような場合は、デフォルトの最下段（pの下の段）が省略されている。

 ---A
  f
 ---B
  p

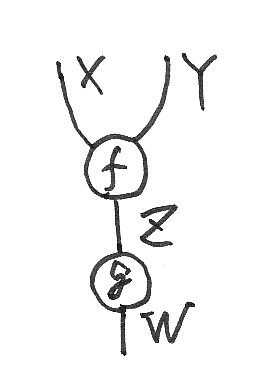
ノードの形状

ノードの形状は、四角、点、丸などがよく使われる。その他の形（例：三角形、ひょうたん形）のノードを使ってもよい。また、形状が意味をもつ（ラベル代わりに形状を使う）場合もある。

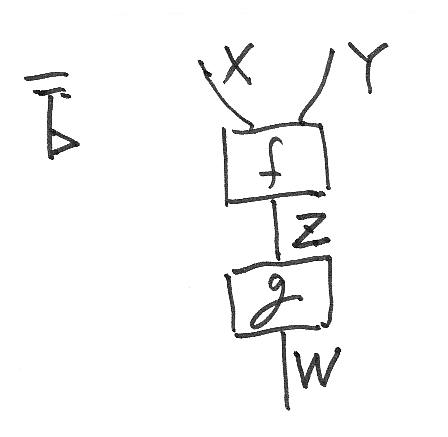
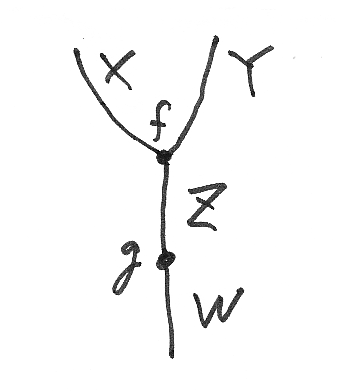
図の引用元

ストリート：

Title: Low dimensional topology and higher-order categories
Author: Ross Street,
URL: http://www.mta.ca/~cat-dist/CT95Docs/LowDim.ps （ポストスクリプトファイル）

ガーナー／シュルマン：

Title: Enriched categories as a free cocompletion
Authors: Richard Garner, Michael Shulman
URL: http://comp.mq.edu.au/~rgarner/Papers/Free-cocomp.pdf

クック：

Title: Quantum Picturalism
Author: Bob Coecke
URL: https://arxiv.org/abs/0908.1787 ; https://arxiv.org/pdf/0908.1787v1.pdf