ノード・ワイヤー図と横棒記法の例と練習 (A2P1) - (保存用) 檜山正幸のキマイラ飼育記メモ編

※この記事は「記事2 問題集1」

ノード・ワイヤー図〈ストリング図〉の解説は：

ノード・ワイヤー図〈ストリング図〉

中学校で習った二元連立一次方程式を例にする。内容は難しくないが、作業（トレーニング）はそれなりに手間がかかる。手間を減らす工夫は各自行ってちょ。

内容：

なぜ練習が必要か
等式系
等式系への操作
事例
練習問題

解答：問題集1の目的と解答と追加説明重要！ (A13R1)

なぜ練習が必要か

次のような図が出てきてもビビらないために、事前に練習が必要である。

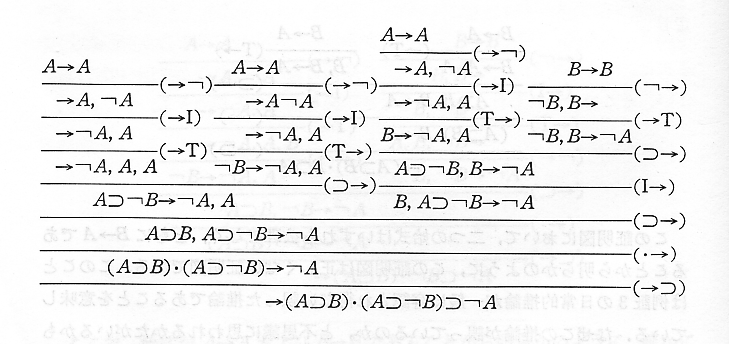
素材としては中学校レベルの内容を扱う。記法（書き方）は、上の図（証明図）と類似の記法を採用する。記法とその記法を使った計算に十分に慣れておかないと、「証明の形式化」でコケる。

等式系

ここでは（あくまでローカルルール）、式とは次の意味だとする。

文字x, yを含むかも知れない1次以下の多項式を単に「式」と呼ぶ。

式の例： 2x - 3y + 1, 2x + 1, -3y, 1

「式 = 式」の形を、ここでは等式と呼ぶ。等式を幾つか（0個でも1個でもよい）縦に並べた形をここでは等式系と呼ぶ。次は等式系の例であり、中学校で習った二元連立一次方程式である。

2x - 3y + 1 = x - 2
x + y = 5

等式系において、等式は上から順に 1, 2, ... と番号をふる。番号は明示的に書いても省略してもどっちでもよい。下の等式系で、左端は番号。

(1) 2x - 3y + 1 = x - 2
(2) x + y = 5

以下では、等式系のi番目の等式を参照するために #i を使う。例えば、#3 は3番目の等式を指す。

等式系への操作

等式系に対して、以下に述べるような操作を考える。操作の説明とともに、横棒記法も説明する。

挿入 Insert

Aを式（x, yを含むかも知れない1次以下の多項式）だとして、与えられた等式系に対して、A = A という自明な等式を最下行に挿入する。この操作を Ins(A) と書く。

例：操作の前

2x - 3y + 1 = x - 2
x + y = 5

この等式系に対して、Ins(x + 1) を行う。

例：操作の後

2x - 3y + 1 = x - 2
x + y = 5
x + 1 = x + 1

これを、横棒記法を用いて、次のように書く。

  2x - 3y + 1 = x - 2
  x + y = 5
 ---------------------- Ins(x + 1)
  2x - 3y + 1 = x - 2
  x + y = 5
  x + 1 = x + 1

上段が操作の前、下段が操作の後。

削除 Delete

与えられた等式系に対して、i番目の等式を削除する。この操作を Del(#i) と書く。

例：

  2x - 3y + 1 = x - 2
  x + y = 5
 ---------------------- Del(#2)
  2x - 3y + 1 = x - 2

フォーク（複製） Fork

与えられた（ひとつの）等式系に対して、まったく同じ等式系をふたつ横に並べる。この操作を Fork と書く。

例：

            2x - 3y + 1 = x - 2
            x + y = 5
 -------------------------------------------- Fork
  2x - 3y + 1 = x - 2    2x - 3y + 1 = x - 2
  x + y = 5              x + y = 5

マージ Merge

与えられたふたつ等式系に対して、左の等式系の下に右の等式系を縦に並べた等式系を作る。この操作を Merge と書く。

例：

  2x - 3y + 1 = x - 2    x + 1 = x + 1
  x + y = 5              y = 3
 --------------------------------------- Merge
       2x - 3y + 1 = x - 2
       x + y = 5
       x + 1 = x + 1
       y = 3

加法 Addition

与えられた等式系のi番目の等式とj番目の等式を、左辺どうし／右辺どうし足して、足した結果の等式を新たにi番目の等式とする。この操作を Add(#i, #j) とする。多項式の足し算は普通に（常識的に）してよい。

  2x - 3y + 1 = x - 2
  x + y = 5
 ---------------------- Add(#2, #1)
  2x - 3y + 1 = x - 2
  3x - 2y + 1 = x + 3

i番目の等式は更新され、他は変わらない。

乗法 Multiplication

与えられた等式系のi番目の等式とj番目の等式を、左辺どうし／右辺どうし掛けて、掛けた結果の等式を新たにi番目の等式とする。この操作を Mult(#i, #j) とする。多項式の掛け算は普通に（常識的に）してよい。Mult(#i, #j) により、1次以下の式でなくなった（ここで言ってる「式」ではなくなった）場合は、等式の左端に NG とマークする。NGマークが付いても、その後の操作を続行してもよい。

（注意：通常は、NGマークが付くような事態になったら、そこで止める。が、続行したい人を私はとめない。ご自由に。）

  2x - 3y + 1 = x - 2
  x + y = 5
 --------------------------------------- Mult(#1, #2)
  NG 2x^2 -xy - 3y^2 + x + y = 5x - 10
  x + y = 5

  2x - 3y + 1 = x - 2
  x + y = 5
  2 = 2
 --------------------------------------- Mult(#2, #3)
  2x - 3y + 1 = x - 2
  2x + 2y = 10
  2 = 2

i番目の等式は更新され、他は変わらない。

事例

次の横棒記法による図は、特に意味はないが、操作の例。

  2x - 3y + 1 = x - 2
  x + y = 5
 ----------------------- Ins(x + 1)
  2x - 3y + 1 = x - 2
  x + y = 5
  x + 1 = x + 1
 ------------------------------------------- Fork
  2x - 3y + 1 = x - 2   2x - 3y + 1 = x - 2
  x + y = 5             x + y = 5
  x + 1 = x + 1         x + 1 = x + 1
                       --------------------- Add(#2, #3)
                        2x - 3y + 1 = x - 2
                        2x + y + 1 = x + 6
                        x + 1 = x + 1
 ------------------------------------------- Merge
  2x - 3y + 1 = x - 2
  x + y = 5
  x + 1 = x + 1
  2x - 3y + 1 = x - 2
  2x + y + 1 = x + 6
  x + 1 = x + 1
 ---------------------- Del(#1)
  x + y = 5
  x + 1 = x + 1
  2x - 3y + 1 = x - 2
  2x + y + 1 = x + 6
  x + 1 = x + 1
 ---------------------- Del(#5)
  x + y = 5
  x + 1 = x + 1
  2x - 3y + 1 = x - 2
  2x + y + 1 = x + 6

練習問題

Ins, Del, Fork, Merge, Add, Mult の操作だけを用いて、二元連立一次方程式 {2x - 3y + 1 = x - 2, x + y = 5} を解け。「解けた」とは、等式系が {x = 定数, y = 定数} の形になったとき。解く過程は、横棒記法による図として記録する。
注意！：移項や代入などのよく知っている操作を無意識にしてしまうことがあるが、許されている操作は Ins, Del, Fork, Merge, Add, Mult だけである。
横棒記法による図をノード・ワイヤー図にせよ。このとき、ノードラベル（操作の名前と引数）は書き込むが、ワイヤーラベル（等式系）は省略してよい。
前問のノード・ワイヤー図を、すべての描画方向（↑→, ↑←, ↓→, ↓←, →↑, →↓, ←↑, ←↓）で描いてみよ。
前問のノード・ワイヤー図をテキスト記法で表現せよ。何もしない操作はidと書くことにする。例えば、前節の例の横棒記法による図は、Ins(x + 1);Fork;(id $\otimes$ Add(#2, #3));Merge;Del(#1);Del(#5) となる。
もし可能なら、自分以外の人に二元連立一次方程式 {2x - 3y + 1 = x - 2, x + y = 5} と、前問のテキスト表現だけを見せて、解く過程を再現できるか確認せよ。
解き方（出来上がる図）は一通りではない。違った解き方も考えよ。
適当な二元連立一次方程式に対して、上の問題群と同じ作業を行え。概念や書き方に慣れるために、幾つか（必要なだけ）の二元連立一次方程式に対して同じ作業を行え。

解答と補足解説

[追記]
冒頭にて：

手間を減らす工夫は各自行ってちょ。

律儀にやってみる経験も必要だけど、手間を減らすヒント：

最後の行を #-1 と書く（一般に、下から勘定する番号をマイナスで書く）と約束すると便利。最後の行（の等式）を削除することは Del(#-1) と書ける。連続した操作は、';'が入ったテキスト記法で書いてもいいとすると、

    …
  -------- Del(#-1);Del(#-1)
    …

これで、最後の2行の削除になる。極論するなら：

    …
  -------- 長いテキスト表現
    …

を許せば、図を極端に短縮できる。

コピー＆ペーストが大量に発生するので、同一な部分を省略する書き方を導入しないと辛い。例えば、注目すべき等式を番号付きで書いてその他は省略とか。

  (3) x + y = 1
  (7=-1) 2 = 2
  ----------------- Add(#3, #-1)
  (1) 3x - 2y = 8
  (3) 2x + 2y = 2
  ----------------- Add(#1, #3)
  (1) 5x = 10

[/追記]

解答：問題集1の目的と解答と追加説明重要！ (A13R1)