このブログは、旧・はてなダイアリー「檜山正幸のキマイラ飼育記 メモ編」（http://d.hatena.ne.jp/m-hiyama-memo/）のデータを移行・保存したものであり、今後（2019年1月以降）更新の予定はありません。

今後の更新は、新しいブログ http://m-hiyama-memo.hatenablog.com/ で行います。

スパイダーグラフ (1)

多圏 Caty トレース／コンパクト閉圏

スパイダーグラフの起原と用途

いつ頃からか、直観主義論理の“ある種の双対”となる論理のシーケント計算をスパイダー計算と呼ぶことにした。そのシーケント計算の絵図的表現がスパイダーグラフ、またはスパイダー図である。スパイダーグラフを使うことにより、スパイダー計算は絵算として遂行できるようになる。

ふと気付けば、スパイダーグラフはCatyScriptの可視化にも使える、つうかピッタリじゃん。CatyScriptプログラムをスパイダーグラフで描けるが、むしろ、スパイダーグラフをプライマリーな存在物と考えて、CatyScriptソースコードはスパイダーグラフのテキストシリアライゼーションに過ぎないと考えたほうがいい。

スパイダーグラフは、テキストコードより意味論（圏論）に近く、抽象度が高く、テキストコードでは表現しにくい制御構造も容易に可視化できる。通常のスクリプトの可視化にも、ハイパーリンク・グラフから作ったWebエミュレーション・グラフの可視化にも汎用的に使える。

参照：

スパイダーグラフの描き方に関する注意

スパイダーグラフは、手描きする場合とソフトウェアによる自動描画（プログラム描き）をする場合がある。手描きとプログラム描き＜ぷろぐらむがき＞では、適切な描き方の基準が異なる。ここでは、基本的に手描き向けの描画法を述べる。が、これは容易にプログラム描きにも適用できることを考慮している。

グラフのノード／辺の個数は、適切な省略により減らすことができる。これは、グラフ書き換え（「描き変え」か？）によるある種の最適化だと言える。このテの最適化にはあまり触れない。描画の原則に注目し、レイアウトや簡略化は別な議論として切り離す。

背景となる圏

意味論の舞台となる圏は、型を対象として計算処理を射とする圏である。Sets-as-Types（Types-as-Sets）の立場なので、「型＝集合」と考えてよい。が、計算は写像ではない。写像では解釈できない作用や効果（モナド類似物; monad-like entities）を持つが、それらはスパイダーグラフにはほとんど現れない（ロバストネス図類似の図で、一部のファシリティを描くことがあるかもしれないが）。

スパイダーグラフには、通常の圏では解釈しにくい概念が出てくるが、それは複圏、余複圏、多圏などで解釈できる。スパイダーグラフは、多圏（polycategory）における計算の可視化である。が、多圏には触れない -- 逆に、多圏とはスパイダーグラフで表現できるような category-like entities と思えばいい。

Caty特有の事情

スパイダーグラフは、Catyへの応用を念頭に置く。Catyの計算モデルは、原則的にデカルト半環圏だが、いくつかCaty特有の事情がある。

  1. void型がある。void型は、デカルト圏の終対象の型だが、それだけでなくて、処理系が自動void結合（後述）を行う。
  2. 射の結合は包含結合である。圏には包含（inclusion）と呼ばれる順序構造（とてもやせた部分圏）⊆があり、cod(f) ⊆ dom(g) なら、射の結合を許す。この結合は通常の圏の結合とは異なる。
  3. 直積の構成法が二種類ある。A×B をJSON配列とJSONオブジェクトの二種類で表現できる。JSONオブジェクトの場合は、プロパティ名（成分ラベル）の選び方に任意性／恣意性がある。

射の描き方

基本的な射は、名前を持つコマンドである。コマンドは、f P :: A -> B の形の宣言を持つ。fが名前、Pはパラメータ型、Aは入力型、Bは出力型である。これを次のように図示する。

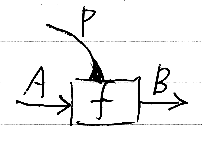
パラメータがないときは描かない。パラメータがあっても、それに注目しないときは描かないことが多い。以下の例では、パラメータを省略している。

射の本体を表すグラフノードを計算ノード（computation node）と呼ぶ。グラフの有向辺はワイヤーと呼ぶこともある。計算ノードにはコマンド名でラベル付けし、ワイヤーには型でラベル付けする。計算ノードの形状はなんでもよい。こだわると身動き取れなくなる。矩形（box）が多く使われるが、手描きでは楕円が描きやすい。データ＆制御の方向を明示するために矢印は付ける。Graphvizならnormal arrow（入出力）、inv arrow（パラメータ）を使う。

void型とnever型

void型とnever型は、それぞれデカルト半環圏の直積単位＝終対象と直和単位＝始対象に対応する。void型、never型を入出力とする射は組み合わせとして4種あるが、neverからの射は描画対象にならない（ソフトウェアでの実現もできない）ので、次の3種となる。

  1. f :: A -> never
  2. f :: void -> B
  3. f :: A -> void

never型は何も描かず、void型は"void"という型ラベルをワイヤーに付ける代わりに点線のワイヤーを使う。

voidとneverの混同と、それによる誤解・混乱が多いので、voidは点線で明示的に描くことにする。

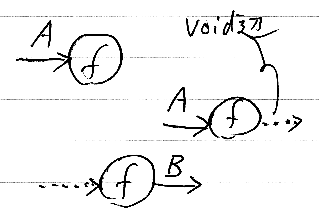
ポイントとスポット

名前を持つ計算ノードは矩形や楕円などの図形として描くが、組み込みの制御構造などの特殊なノードは別な形状を使うことがある。例えば、分岐に関しては次のような図示法があり得る。

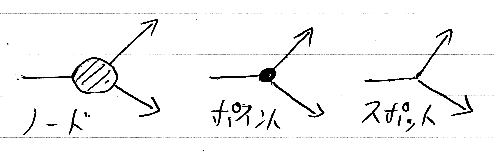
形状を持つ図形の代わりに、点（point）を使って描くノードをポイント、何も描かない（none）ときはスポットと呼ぶ。ポイントもスポットもその意味は射であるし、グラフのノードに代わりはないが、特殊なノードを示すときに使われる。

型と型制約

ワイヤー（グラフの有向辺）は、型でラベルする。ラベルの描画法には次の2つがある。

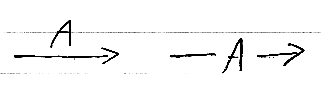
右側の描き方は、辺ラベルが他の意味で使われているときや、型を強調したいときに用いる。

Catyの包含結合（パイプ結合）では、ワイヤーの両端の型が違うケースも許す。しかし、包含関係は要求するので、そのことを次のように表す。

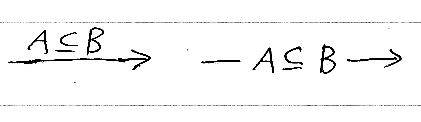
「A⊆B」の形の式を型制約と呼ぶ。単一の型Aも「A⊆A」とみなせるので、スパイダーグラフのワイヤーは型制約でラベルされていると言える。

恒等射とvoid射

圏論では、対象Aの恒等射は idA、対象Aから終対象への唯一の射を !A と書く。Catyでは、pass<A>, void<A> である。

恒等射は特別な事情がない限りは計算ノードとしては描かない。型が不明な pass はラベルがないワイヤー、pass<A> は型Aをラベルしたワイヤーとして描く。

void射も、実線と点線を繋いだワイヤー（混合ワイヤー）として描く。型が不明な void はラベルがない混合ワイヤー、void<A> は型Aをラベルした混合ワイヤーとして描く。

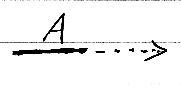
不明な型、未定な型、型に注目してないことを明示的に表すには、dont-care型マーカー '_' （アンダースコア）を型ラベルに使う。'_'は、出現ごとに違う型で具体化可能な型変数である。

結合の描き方

Catyのスパイダーグラフでは、3種類の射の結合方法がある。

  1. 厳密結合 -- 圏論の結合である。cod(f) = dom(g) のときだけ結合が許される。
  2. 包含結合 -- cod(f) ⊆ dom(g) のとき結合が許される。
  3. void結合 -- 任意のfと dom(g) = void であるgの結合が許される。

それぞれ次のように図示される。下向きの⇒は、結合操作の実行を示す。

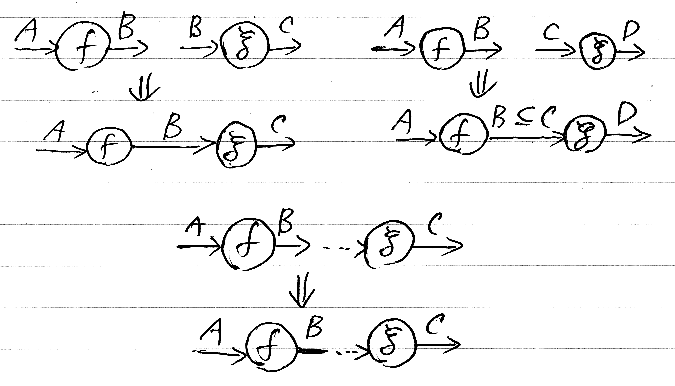
Catyの結合は常に包含結合で、厳密結合を指定する方法はない。fとgのvoid結合は f;g と書く。明示的なvoid結合記号「;」を書かなくても、gのdomを見て処理系がvoid結合に切り替えることがある。これが自動void結合である。自動void結合は、便利なソフトウェア的な機能であるが、意味論としては、void射を挿入するだけである。

スパイダーグラフ上では、明示的なvoid結合と自動void結合を区別することはできない。どちらも同じように混合ワイヤーで図示される。

ジャンクションの描き方

組み込みの制御構造を表す特殊ノード（特殊射の図式表示）をジャンクションと呼ぶ。恒等射を表すワイヤー、void射を表す混合ワイヤーもジャンクションである。その他に次のジャンクションを使う。

  1. コピージャンクション -- デカルト圏の対角Δに対応する多圏の射。
  2. タプリングジャンクション -- タプルを構成するコンストラクタに対応する。配列構成とオブジェクト構成がある。タギングも一種のタプリングである。
  3. 排他的分岐ジャンクション -- CatyScriptの排他的ユニオン型とwhen分岐に対応する。
  4. 合流ジャンクション -- 制御＆データの合流（待ち合わせはしない）に対応する。

これらのジャンクションは、一例として次のように描く。

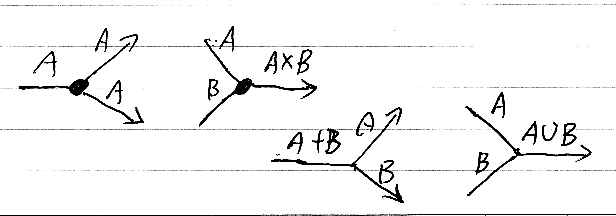
とりあえず、コピーとタプリングはポイント、排他的分岐と合流はスポットを使ったが、他の描画法を採用するかもしれない。

スパイダー射

A, B1, B2, ..., Bn を型として、スパイダー射は次のようなプロファイルを持つ（多圏の）射である。

  • f :: A -> B1, B2, ..., Bn

これは、直観主義論理のシーケントの左右を逆にした形をしている。排他的とは限らないユニオン型を∪で表すとして、上記のスパイダー射は、f :: A -> (B1∪B2∪ ... ∪Bn) と似てるが異なる。グラフノードとして、「出る辺の数が違うので違う」と思っておけば当面は十分である。

スパイダー射に対応するノードをスパイダーノードと呼ぶ。スパイダーノードは、多圏（polycategory）の射を表す。

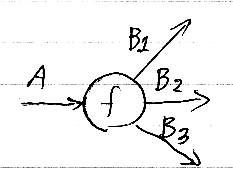
スパイダーノードから出る辺（出力ワイヤー）の本数は任意だ（0本でもよい）が、入力ワイヤーは1本（voidワイヤーでもよい）である。このため、片側スパイダーノードとも呼ぶ。

入力ワイヤーを複数持つ射（計算ノード）を認めるが、略記（省略形）として導入する。合流ジャンクションとスパイダー射の結合（包含結合）を簡略に描いた図形が両側スパイダーノードである。

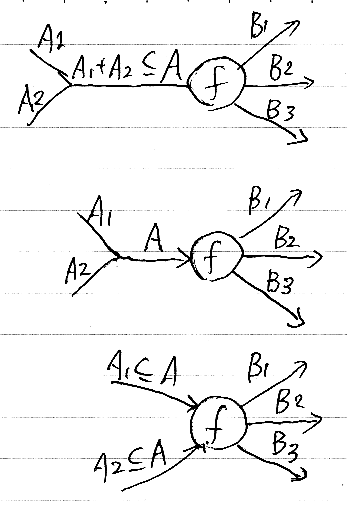
スパイダーグラフ内では両側スパイダーノードを使うが、厳密な議論のときは、合流ジャンクションと片側スパイダーノード（本来のスパイダー射）の結合に戻して考える必要がある。両側スパイダーノードは便宜上の図示法である。が、図をすっきりさせる効果は大きい。

リテラル射の描き方

データインスタンスの集合Xが定まっているとして、Xを基本データ領域と呼ぶ。Xの要素はリテラル表現を持つとする。Catyの場合は、基本データ領域Xは、リテラル表現を持つスカラー全体の集合である。Xに属するデータインスタンスxとそのリテラル表現はしばしば同一視される。

x∈X に対して、Singleton(x) = {x} とする。Singleton:X→Pow(X) である。Types-as-Sets なので、Pow(X)の要素（＝Xの部分集合）は型である。一方、x∈X に対して、literal(x) :: void -> Singleton(x) というコマンド（射）を定義できる。

  • literal(x)(null) = x

literal(x) を、データインスタンスxのリテラル射と呼ぶ。リテラル射は、xのリテラル表現をラベルとする計算ノードとして描かれる。ただし、出力型は Singleton(x) に決まっているのでラベルしなくてもよい。（以下の図の出力形は、{"hello"} というシングルトン型。）

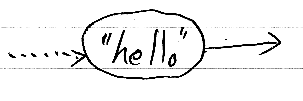
変数の描き方

Catyでは、変数の生成と参照が次のようにして行える。

  • 変数の生成 > foo
  • 変数の参照 %foo

「>」が変数生成の演算子、「%」が変数参照の演算子となっている。変数生成はワイヤー上に乗った変数ポイントで表す。型Aの変数参照は、void -> A の計算ノードとして表すが、変数ポイントからの変数参照ワイヤーを描く。変数参照ワイヤーは、通常のワイヤーとは区別される。プログラム描きのときはワイヤー（有向辺）の色を変える。モノクロ手描きのときは、適当な間隔で短い斜め棒を添えて変数参照ワイヤーを識別する。斜め棒は、「制御はこのワイヤーを通らない」という意味合いである。

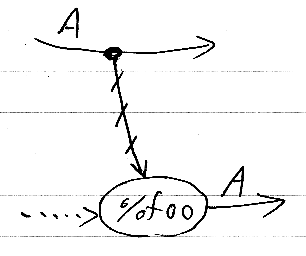
スパイダーグラフの書き換え操作により、変数ポイントをコピージャンクションに置き換え、変数参照ワイヤーを通常ワイヤーに置き換え、変数参照ノードをすべて消し去ることができる。変数を消し去っても挙動は変わらないようにできるが、テキストコードでは変数の必要性が高い（経験上、変数なしではとても書きにくい）。

続きは

「スパイダーグラフ (2)」では、スパイダー射の意味論、エリアやポートについて述べる。