型検査と制約解決:不等式的な型付けと制約系(連立不等式系)
不等式的な型付けとは、ワイヤー(パイプ)が1本あると、その両端に型がラベルされる型付けの方法。普通の圏論だと、f:A→B, g:C→D が結合可能なのは B = C のときだけだが、Catyでは B = C は要求しない。B ⊆ C という集合の包含に関する不等式を要求する。したがって、fのボックスとgのボックスを繋ぐワイヤーには、「左にB、右にC」というラベルが貼られる。それで、B⊆C という不等式も添えることになる。
下の図は、ワイヤーに2つの型をラベルして制約の論理式(不等式)を書いたもの。
制約の論理式:
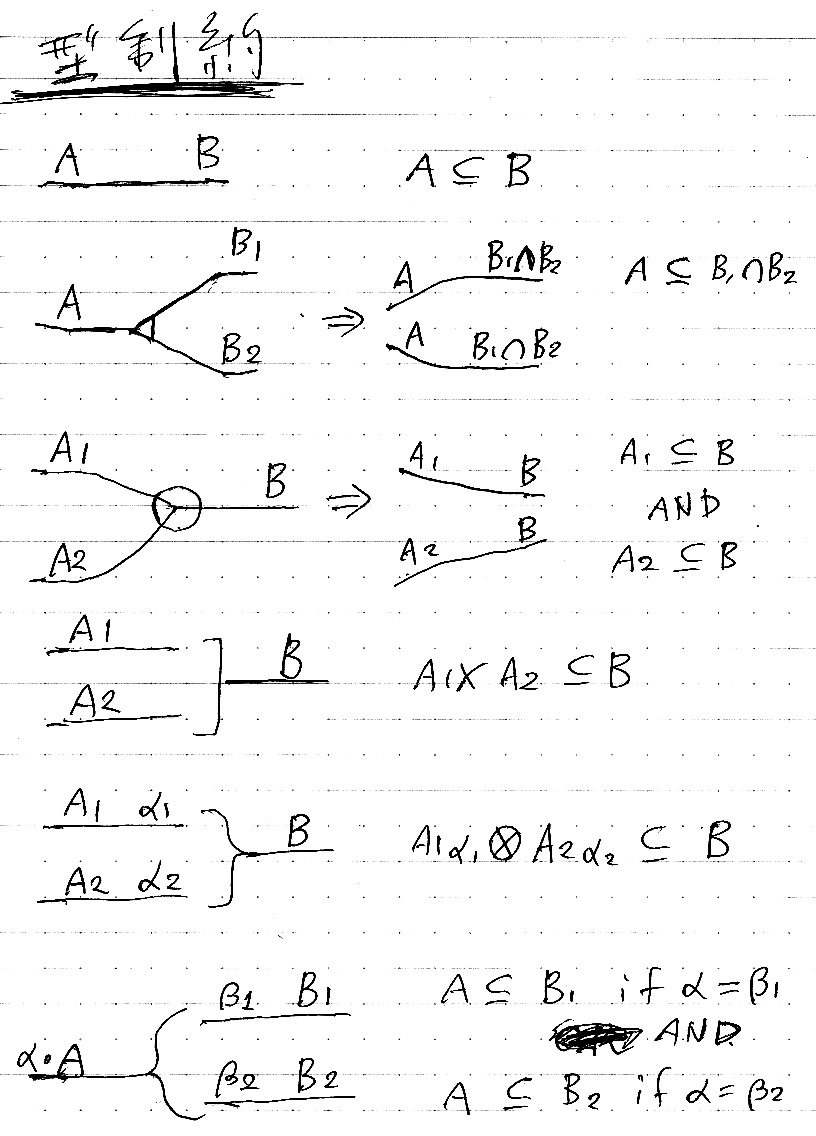
原寸大
基本的な型構成子は:
- 集合のミート(共通部分)
- 直積
- 直積ラベリング(Aとαから Aα を作る)
- ラベル付き直積
- 直和ラベリング(Aとαから α・A を作る)
- ラベル付き直和
Catyでの記法は:
- &
- [-, -]
- {-: -} または {- >:-}
- ++
- @- - または - >@ -
- |
&, ++, | は中置二項演算子で、結合的演算。++, | は全域的に定義されていない。>@ も中置二項演算子なのだが、少し変わっているかな。
このような構成子(演算、関数)と包含の不等号を扱う論理系をSILと呼ぶ。以下にSILの解説。
SILは2つのソートを持つ。型(集合と言っても同じ)とラベルが2つのソート。基本記号は次のとおり。
- 型定数
- 型変数(x, yなど)
- 型演算子、型関数
- 型関係記号 ⊆
- ラベル定数(たくさん)
- ラベル変数(α、βなど)
- ラベル関係記号 =、≠
- 型とラベルの演算記号 ・と_(下付き添字の代わり)
- 括弧
通常の方法で型項とラベル項が定義できる。ラベル項はラベル定数かラベル変数。原子論理式は:
- 型論理式 ::= 型 ⊆ 型
- ラベル論理式 ::= ラベル = ラベル | ラベル ≠ ラベル
一般の論理式は:
- 型論理式 ::= 原子論理式 | 型論理式 ∧ 型論理式 | 型論理式 if ラベル論理式 | ∀x,y.型論理式 など
- ラベル論理式 ::= 原子ラベル論理式 | ラベル論理式 ∧ ラベル論理式 | ∀α.ラベル論理式 など
論理式からシーケントを作って、シーケント計算の体系を作ればいい。公理系はデクスター・コゥゼンが揃えている。
SILのなかで論理計算を行えばそれなりの効果はあるだろうが、とりあえずはSIL使わなくてもいいかな、と。