型検査と制約解決:制約解決=連立不等式系の解を求める
制約解決の部分は今までいいかげんでしたね。そもそも、連立不等式系なので、解があっても一意的に決まるわけではない。なにか「最適性」の基準を決めて、「制約(不等式の集まり)を満たしてコレコレを最大にする」ような最適解の問題にできればいいのだけど、「なにが最適か?」もハッキリしない。
という事情で、解けるかもしれないが、見つかった解がいいか悪いかわからん、という状態だった。それはまー今でも変わらないのだけど、あまり複雑でなくて、「悪くない解」が見つかるアルゴリズムで妥協する。
下の図にだいたいのステップを書いている。単一化の結果から二部グラフ(無向、有向の混合グラフ)を作って、それを全部つないだグラフ内で計算を行う。そのグラフは、変数間の制約を記述したグラフ。このグラフの部分グラフを制約の伝搬フローとみなして、ダイクストラアルゴリズムで暫定解を求める。暫定解が残りの条件を満たすかを後からチェックする方針。
制約伝搬フローグラフを作るとき、片方向(one-way)だけを考えるので、片方向伝搬法(one-way propagation method)とでも呼んでおこう。片方向伝搬法は、片方向(絵では右から左)しか考慮しないので、あまり精度が高くない。が、まーいい、妥協、妥協。
制約伝搬フローグラフにサイクルがあっても大丈夫だと思うが確認してない。たぶん、最大不動点(最小不動点ではない)を取ればいいだろう。
制約解決の方法:
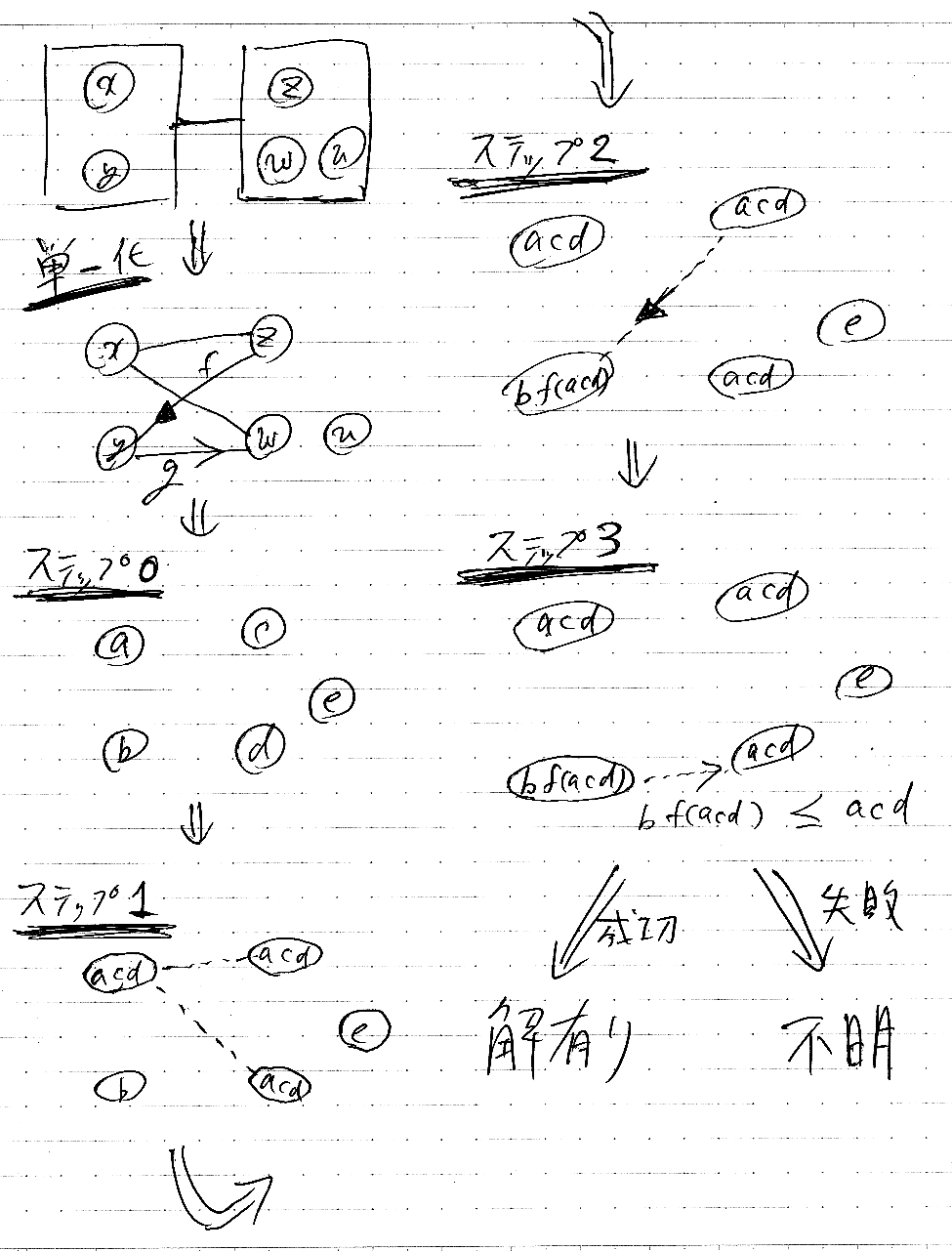
原寸大
上の図に間違いがあったり、後から考えが変わった部分もある。が、順に説明していく。
単一化
箱はコマンド、線がワイヤー=パイプを表す。コマンドが総称プロファイルを持っているとき、その型変数を箱のなかに丸で描くとする(描き方はなんだっていいが)。本来、総称プロファイルに出現する型変数はラムダ束縛されているので、変数名はいくら変えてもいい(アルファ変換)。アルファ変換をして、全体として同じ変数名が現れないようにしてからラムダ束縛を解除する。つまり、自由変数のように扱う。まえもってアルファ変換をしておけば、本来違う変数が同じ名前になることはない。ぜーんぶ違う変数として扱う。
絵には描いてないが、ワイヤーの左右に総称型のラベルが貼ってある。例えば左がS(x,y)、右がT(z,w,u)のように。単一化は、S(x,y)とT(z,w,u)に関して行う。単一化が成功すれば、その結果は、変数 x, y, z, w, u のあいだの不等式の集合(空集合かもしれない)となる。
絵の例では:
- x⊆z
- y⊆f(z)
- x⊆w
- g(y)⊆w
を想定している(一例として)。
「変数⊆変数」の形の不等式だけ特別扱いして、無向辺で変数どうしを繋いでいる。が、この特別扱いは不要だった気がする。ステップ1もおそらく不要だろう。
y⊆f(z) の形のとき、「zの制約がfを通してyに伝搬する」という意味で zからy に矢印を描いている。これを伝搬辺と呼ぼう。yからwの辺も同じなのだが、こっちの伝搬は無視する。片方向伝搬法と名付けた由来は片方しか見ないから。g(y)⊆w は無視してしまう。右から左 -- コドメインからドメインを制約する方向だけに注目する。
変数の値と関数
説明の順序が前後するが、片方向伝搬法では、型とか集合とかはもう考えない。変数は値で具体化される、というだけ。値は最小限を持つミート半束の要素だとする。ミート半束のミートは∧で表すが、a∧b は単に a b とか ab とも書く。
ミート半束に値を持つ定数、変数、関数が登場する。関数は単調なものに限る。特に、関数は最大値を最大値に移す。
最大値による初期化
各変数には、許される変域があり、その変域(定義域)は最大値を持つ。変数の変域の最大値を、その変数の最大値と呼ぶ。
最初は、すべての変数をその最大値で初期化する。絵の例では:
- x := a
- y := b
- z := c
- w := d
- u := e
連結成分の変数達は同じ値にする
x⊆z, x⊆w のような形で関連する変数は、無向辺で結んである。この無向辺による連結成分を求めて、同じ連結成分に属する変数はすべて同じ値にする。その値は、連結成分内のすべての変数のミートを取った値である。
- x = acd
- z = acd
- w = acd
伝搬の影響を計算する
右から左に向かう辺だけを取り出して、その部分グラフ上で伝搬の影響を累積する。
上の絵では、2つの箱と1本のワイヤーしか出てこないが、すべての箱とワイヤーからグラフを作るのでグラフは大きくなるかもしれない。そのグラフ上で、伝搬関数を成分とする正方行列を作って、クリーネ・ファインマン型の累積値を計算する。
この状況では、… またも出ましたダイクストラ・アルゴリズム。ダイクストラ波動を発進させる境界(有向グラフのルート領域)を求めて、そこから累積値を計算する。普通は積和を計算するが、半束なのでミートしか演算がない。しいていえば、辺上の関数による計算が積で、ミートを和とする総積和となる。
残っていた条件のチェック
左から右への矢印は無視していたので、ダイクストラ波動を走らせた後でチェックする。このチェックのときは、変数はすべて具体化されているので、具体値の不等式チェックとなり、真偽が決定する。
チェックで不等式偽となっても、それで完全にダメということではない。暫定解と整合しないだけで、暫定解を少し変えれば不等式を満たす可能性がある。が、暫定解を変えることはしないで、事後チェックが失敗した部分だけ実行時チェックにする。
注意
ステップ3のチェックに入る前に、暫定解において値が0(最小値)になる変数がないかのチェックを入れるのが普通。0は、普通は空集合を意味し、たいていは具合が悪い。その他、チェックすることはあるかもしれない。
型変数はもとの総称形における出現位置から、パス式を持つ。このパス式を使えば、実行時チェックを軽くできる可能性がある。CatyScript+eのパス毎のバリデータはそのような用途を想定している。
制約伝搬グラフにサイクルがあるとき、μオペレータの逆であるνオペレータを使えばいいと思う。νオペレータは最大不動点演算子だが、最大不動点の存在を示す必要はあるな。
最後に
片方向伝搬法は、制約条件の半分(? 方向から言えば半分)を捨ててしまうので、ちょっとヒドイとも言えるが、実際的にはこれでたいていは間に合ってしまうのではないかなー。メインになるのはロビンソン・アルゴリズムとダイクストラ・アルゴリズムだけど、記号処理やグラフ変形を多用するので、それほど簡単とも言えない。ここらへんがいい落とし所だと思っている。