このブログは、旧・はてなダイアリー「檜山正幸のキマイラ飼育記 メモ編」（http://d.hatena.ne.jp/m-hiyama-memo/）のデータを移行・保存したものであり、今後（2019年1月以降）更新の予定はありません。

今後の更新は、新しいブログ http://m-hiyama-memo.hatenablog.com/ で行います。

シーケントとスコット・ブラケット (A10P8)

RSS練習問題

※この記事は「記事10 問題集8」

シーケントはゲンツェンにより導入された概念であり、（数学の一分野としての）論理が扱う主要な対象物（のひとつ）である。論理式が論理の主役なのではない。

  • 論理式は、論理式のリストを構成する素材に過ぎない。
  • 論理式のリストは、シーケントを構成する素材に過ぎない。

とりあえずは、シーケントとシーケントが表すもの（推論やそのプロファイルなど）を論理の主役と捉えよう（ただし、シーケントも主役の座を奪われる事態も想定しながら）。

これより前に行うべき練習は：

  1. 命題と、そのコンテキスト／真理集合
  2. 命題のリストの扱い方

[追記]「形式化」を「型式化」と誤字っていたので過去に遡って修正。かな漢字変換は、一度間違えると誤字を学習して使い続けるから怖い。[/追記]

内容：

  1. ゲンツェンのLKシーケント計算をご存知の方への注意
  2. シーケントとは何であるか
  3. シーケントの別な書き方
  4. 正規形シーケントとコンテキストの共通化
  5. 左選言的シーケント
  6. シーケントのスコット・ブラケット
  7. 計算練習のやり方
  8. 組み込み推論を表すシーケント

関連する記事：

  1. シーケントに親しもう (A11P9)
  2. ともかくシーケントなんだから、頼むよ、皆んな (A12)

ゲンツェンのLKシーケント計算をご存知の方への注意

検索などでたまたまここに辿り着いた人が誤解するのも困るので、毎回この節を冒頭に置くことにする。

  1. '⇒'は含意〈条件法〉の論理結合子で、'→'がシーケントの左右を区切る記号である。
  2. ゲンツェンのLKシーケントでは、左辺のカンマは連言的に、右辺のカンマは選言的に解釈をする。ここでのシーケントでは、出現位置の情報を使わずに、カンマは常に連言的であり、選言的な区切り記号に縦棒'|'を使う。
  3. (x∈R, n∈N) のような書き方は、集合論の命題ではなくて、自由変数の型宣言（のリスト）である。自由変数の型宣言のリストをコンテキストと呼ぶ。
  4. 暗黙のコンテキストを使う場合もあるが、できるだけ、シーケント内に明示的にコンテキストを書き込むようにしている。

シーケントとは何であるか

シーケントとは何であるかを一言で説明するのは難しい。とりあえず、左連言的シーケントの形から入る。

左連言的シーケントは、コンテキストとコンテキストなし命題をカンマ区切りで並べたものを左辺として、コンテキストなし論理式のリスト（連言的でも選言的でもよい）を右辺とした形式で、左辺と右辺の区切り記号には'→'を使う。

  • 例： (n∈Z), n ≧ 0, (a∈R), (a ≧0 ∧ ∃k∈Z.(n = 2k)) → ∃x∈R.(xn = a)

コンテキストを α, β など、コンテキストなしの論理式を A, B, C などで表す。上の例は、次の形をしたシーケントである。

  • α, A, β, B → C

ここで：

  1. コンテキストαは、(n∈Z)
  2. 論理式Aは、n ≧ 0
  3. コンテキストβは、(a∈R)
  4. 論理式Bは、(a ≧0 ∧ ∃k∈Z.(n = 2k))
  5. 論理式Cは、∃x∈R.(xn = a)

習慣として、リストを囲む括弧は書かない。

左連言的シーケントは、次の条件を満たす必要がある。

  • 論理式の自由変数は、それより左にあるコンテキスト内で型宣言されてなくてはならない。

上の例で：

  1. 論理式Aに出現する自由変数 n は、コンテキストαで型宣言されている。
  2. 論理式Bに出現する自由変数 a は、コンテキストβで型宣言されている。
  3. 論理式Cに出現する自由変数 n, a は、コンテキストαとβで型宣言されている。
  4. 論理式Cに出現する束縛変数 x は、自由変数でないので、事前に型宣言する必要はない。

※注意： すべての束縛変数は、限量子のなかで型宣言される。我々の演繹システムでは、型不明の束縛変数は存在しない。

次の条件は実は必須ではない。プログラミング言語などでは、むしろ邪魔になる。が、話を簡単にするためにこの条件を守ることにする。

  • シーケントに出現するコンテキストはコンフリクトしてはならない。

※注意： プログラミング言語で言えば、上記条件は、ネストしたスコープにおいてシャドーイングを禁止することで、採用しないことが多い。コンフリクトしても、右側を優先すれば問題は起きない。

α, A, β, → B のように、左辺の一番右がコンテキストのときは、混乱を避けるためにカンマを書いておく（ここだけの書き方の約束）。真命題Tを足して、

  • α, A, β, T → B

の略記だと解釈する。

シーケントの別な書き方

左連言的シーケントは、キーワードを使って自然言語風に書かれることがある。(n∈Z), n ≧ 0, (a∈R), (a ≧0 ∧ ∃k∈Z.(n = 2k)) → ∃x∈R.(xn = a) なら、



For n∈Z

Given n ≧ 0

For a∈R

Given a ≧0 ∧ ∃k∈Z.(n = 2k)

Holds

   ∃x∈R.(xn = a)

End

この書き方から類推されるように、シーケントは、定理記述の形式化として使える。コンテキストのイメージを心に持ちたい人は、「それは、定理記述の形式なのだ」と捉えてもよい。

ただし、シーケントはあくまで形式であり、シーケント形式で表現できるものは色々とある。つまり、シーケントの用途と解釈は多様である。特定の用途に強く固定するのは好ましくない。

[追記]シーケントについて、もっと具体的なイメージを持ちたい人は次の記事を参照。

[/追記]

正規形シーケントとコンテキストの共通化

コンテキストが一番左に一回だけ出現するシーケントを、ここでは正規形シーケント〈sequent of {canonical | normalized} form〉と呼ぶ。コンテキストが複数回出現する場合は、それらのコンテキスト達をすべて連接してまとめたものを左端に置くと正規形になる。正規形を作るこの操作を正規化と呼ぼう。

※注意： コンテキストがない論理式は解釈不能なので、いかなる場合でもコンテキストは書く。論理式が自由変数をまったく持たない場合でも空コンテキストが在ると考える。

(n∈Z), n ≧ 0, (a∈R), (a ≧0 ∧ ∃k∈Z.(n = 2k)) → ∃x∈R.(xn = a) の正規形は：

  • (n∈Z, a∈R), n ≧ 0, (a ≧0 ∧ ∃k∈Z.(n = 2k)) → ∃x∈R.(xn = a)

いま、n個の正規形シーケントがあり、それらを

  • i番目のシーケントのコンテキストを αi
  • i番目のシーケントの左辺の論理式リストを Γi
  • i番目のシーケントの右辺の論理式リストを Δi

とすると：

  • 1番目のシーケントは α1, Γ1 → Δ1
  • 2番目のシーケントは α2, Γ2 → Δ2
  • … …
  • n番目のシーケントは αn, Γn → Δn

と書ける。

異なるシーケントのコンテキストがコンフリクトすることはある。例えば：

  1. (x∈R), x ≧ 0 → ∃y∈R.(y2 = x)
  2. (x∈N), ¬(x = 0) → ∃y∈N.(y + 1 = x)

このような場合、シーケント全体に変数リネームを施すとコンフリクトを回避できる。

  1. (x∈R), x ≧ 0 → ∃y∈R.(y2 = x)
  2. (n∈N), ¬(n = 0) → ∃y∈N.(y + 1 = n) （xからnにリネーム）

したがって、

  • n個のシーケントがあるとき、必要なら変数リネームを施せば、コンテキスト達 αi（i = 1, 2, ..., n）はコンフリクトしないと仮定してよい。

コンフリクトしないn個のコンテキスト達の連接をαとする。

  • α := α1#α2#...#αn

それぞれのシーケントのコンテキストを水増し〈thinning〉してαにすると、

  • 1番目のシーケントは α, Γ1 → Δ1
  • 2番目のシーケントは α, Γ2 → Δ2
  • … …
  • n番目のシーケントは α, Γn → Δn

すべてのシーケントのコンテキストが共通なので、共通コンテキストαを省略していいとすると：

  • 1番目のシーケントは Γ1 → Δ1
  • 2番目のシーケントは Γ2 → Δ2
  • … …
  • n番目のシーケントは Γn → Δn

多くの教科書・論文で、このような処理を事前に行うことを（暗黙の）前提として、コンテキストは無視して話を進める方法が採用されている。しかし、演繹システムのソフトウェア実装をまじめに考えるときなどは、「コンテキストは無視しよう」なんてことが許されるはずもなく、コンテキストの扱い方を綿密に検討・設計しなくてはならない。

とはいえ、毎度毎度コンテキストを明示するのが鬱陶しいのも事実なので、ここでは、コンテキストに関する言及がないときは、すべてのシーケントに共通する大域的コンテキスト〈global context〉が背後に存在することを仮定する。もちろん、必要があれば、明示的にコンテキストを記述する。

左選言的シーケント

左選言的シーケントは、左辺を選言的リストにしたシーケントである。コンテキストとコンテキストなし命題を縦棒区切りで並べたものを左辺として、コンテキストなし論理式のリスト（連言的でも選言的でもよい）を右辺とした形式で、左辺と右辺の区切り記号には'→'を使う。

正規形の左選言的シーケントは、

  • α | A1 | ... | An → Δ

左辺の論理式が0個のときは、

  • α | → Δ

となるが、偽命題⊥を足して、

  • α | ⊥ → Δ

の略記だと解釈する。

左選言的シーケントは、実際に使われることが稀で、最初から採用してない演繹システムが多い。が、我々の演繹システムでは左右を対称に扱うので、左選言的シーケントも必要になる。

左連言的シーケントでも左選言的シーケントでも、コンテキストも命題も同じように（特に区別せずに）並べるが、これは恣意的な記法で、コンテキストは別な囲み記号／区切り記号を使って区別するような構文も考えられる。区切り記号としてカンマまたは縦棒をそのまま使っているのは、単に「簡略だから」以上の理由はない。

もっと言えば、例えば、α, A, B, β, C → D | E というシーケントが表す構造は下の絵のようなものであり、所詮、簡素なテキスト表現ではうまく伝達できないものである。（下の絵や描き方は、いずれ詳しく説明するから、今は気にする必要はない。）

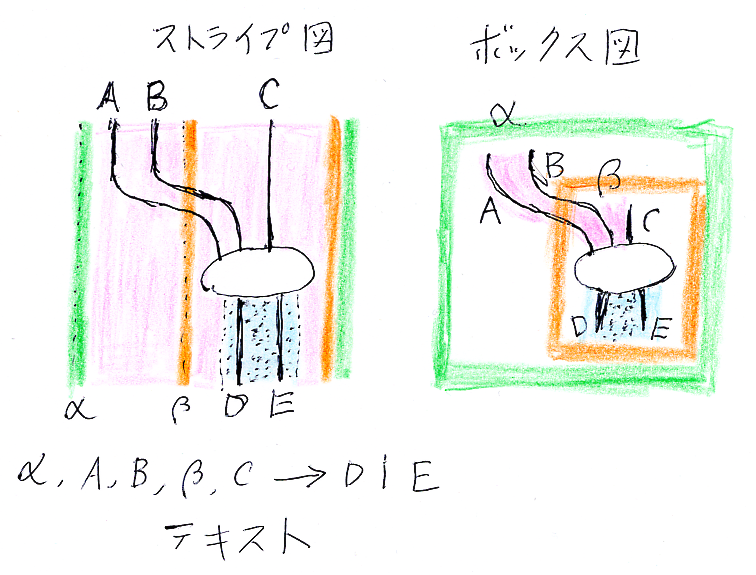
この図は、論理式をワイヤーで描き、論理式のリストは次のようなケーブルとして描く描画法による。

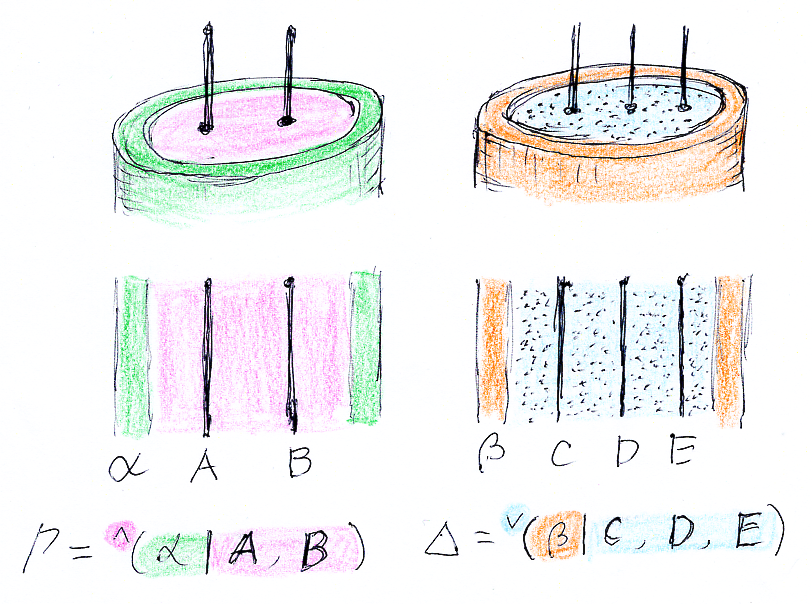
「リアルな電線」も参照。

シーケントのスコット・ブラケット

※注意： Sが集合Xの部分集合のとき、Scは、XにおけるSの補集合を表す。

正規形シーケントに対して、そのスコット・ブラケットを定義する。

正規形左連言的シーケントは、

  • α, A1, ..., An → Δ

これのスコット・ブラケットは、

  • 〚α, A1, ..., An → Δ〛 := 〚∧(α| A1, ..., An)〛c∪〚Δ〛

ここで、〚Δ〛は、コンテキストをαとして計算したリストΔのスコット・ブラケットである。

左辺論理式が0個のときは、

  • α, T → Δ

と解釈するので、

  • 〚α, T → Δ〛 := 〚∧(α| T)〛c∪〚Δ〛 = 〚Δ〛

正規形左選言的シーケントは、

  • α | A1 | ... | An → Δ

これのスコット・ブラケットは、

  • 〚α | A1 | ... | An → Δ〛 := 〚∨(α| A1, ..., An)〛c∪〚Δ〛

ここで、〚Δ〛は、コンテキストをαとして計算したリストΔのスコット・ブラケットである。

左辺論理式が0個のときは、

  • α | ⊥ → Δ

と解釈するので、

  • 〚α | ⊥ → Δ〛 := 〚∨(α| ⊥)〛c∪〚Δ〛 = Dom(α)

正規形ではないシーケントのスコット・ブラケットは、正規形に直してから上の定義に従って計算する。

計算練習のやり方

シーケントとそのスコット・ブラケットに慣れるための練習問題は各自作ってみて。

  1. 論理式を何個か準備する。例えば、「命題のリストの扱い方」の「題材に使う論理式」にある40個の論理式。
  2. 論理式を何個か選んで（0個でもよい）、連言的または選言的リストにして左辺とする。
  3. さらに論理式を何個か選んで（0個でもよいが、Tか⊥に置き換えたほうが分かりやすい）、連言的または選言的リストにして右辺とする。
  4. 選んだ論理式の変数がすべて型宣言されるようにコンテキストを作る。型〈変数の変域〉は、N, Z, Q, R から適当に選ぶ。
  5. そのコンテキストを左端に添えて、正規形シーケントとする。
  6. 作ったシーケントのスコット・ブラケットを定義に従って計算する（そして、図示する）。

組み込み推論を表すシーケント

シーケントが正しいとは、シーケントの（正規化したときの）コンテキストをαとして、

  • そのシーケントのスコット・ブラケットの値が Dom(α) であること。

問題： 論理式 A, B が何であっても、以下のシーケントが正しいことを確認せよ。

  1. α, A → A
  2. α, A, A⇒B → B
  3. α, A → T
  4. α, A∧B → A
  5. α, A∧B → B
  6. α, A → A, A
  7. α, A, A → A
  8. α, A, T → A
  9. α, A → A, T
  10. α, A, B → B, A
  11. α, A, B → A∧B
  12. α, A∧B → A, B
  13. α | ⊥ → A
  14. α | A → A∨B
  15. α | B → A∨B
  16. α | A | A → A
  17. α | A → A | A
  18. α | A → A | ⊥
  19. α | A | ⊥ → A
  20. α | A | B → B | A
  21. α | A∨B → A | B
  22. α | A | B → A∨B

これらのシーケントは、我々の演繹システムの組み込み推論を表すシーケントである。αは、すべてのシーケントに共通する大域的コンテキストだから省略してもよい、という習慣を使えば、我々の組み込み推論（を表すシーケント）は次のように書ける。

  1. A → A
  2. A, A⇒B → B
  3. A → T
  4. A∧B → A
  5. A∧B → B
  6. A → A, A
  7. A, A → A
  8. A, T → A
  9. A → A, T
  10. A, B → B, A
  11. A, B → A∧B
  12. A∧B → A, B
  13. ⊥ → A
  14. A → A∨B
  15. B → A∨B
  16. A | A → A
  17. A → A | A
  18. A → A | ⊥
  19. A | ⊥ → A
  20. A | B → B | A
  21. A∨B → A | B
  22. A | B → A∨B

横棒記法で縦書きにすれば（もはや、形はシーケントではないが）：

1.
  A
 ---
  A

2.
  A  A⇒B
 --------
    B

3.
  A
 ---
  T

4.
  A∧B
 ------
   A

5.
  A∧B
 ------
   B

6.
   A
 -----
 A  A

7.
 A  A
 -----
   A

8.
  A  T
 -----
   A

9.
   A
 ----
 A  T

10.
 A  B
 -----
 B  A

11.
 A  B
 -----
 A∧B

12.
 A∧B
 -----
 A  B

13.
  ⊥
 ---
  A

14.
   A
 -----
 A∨B

15.
   B
 -----
 A∨B

16.
 A | A
 -----
   A

17.
   A
 -----
 A | A

18.
   A
 -----
 A | ⊥

19.
 A | ⊥
 -----
   A

20.
 A | B
 -----
 B | A

21.
 A∨B
 -----
 A | B

22.
 A | B
 -----
 A∨B

横棒記法ではカンマではなくて空白で論理式を区切るのも単なる習慣で意味はない。