型検査と制約解決:ジャンクション
お絵描き圏論とCatyScriptの変数など - 檜山正幸のキマイラ飼育記 とか 変数なしプログラミングとお絵描き圏論 - 檜山正幸のキマイラ飼育記 とかにデータフローグラフの例はある。ボックス&ワイヤーの絵を描けばいいのだが、ワイヤリングのための特殊なノードとしてジャンクションてのがあるから、これを説明しておく。
ジャンクション:
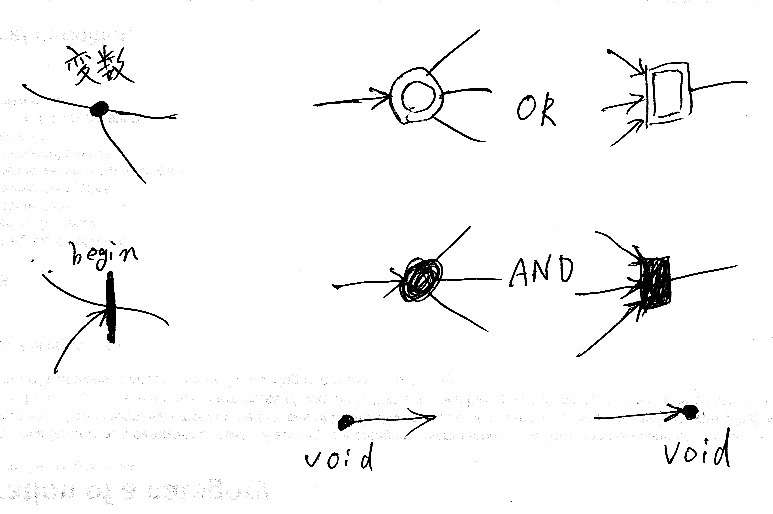
原寸大
コピーとジョインはいいとして、そこから下は説明のテキストが変だな。
- ペア、タプル、ラベル付きタプル: 射のデカルトペアやデカルトタプルを作るときの右半分の絵で、この絵自体は直積とラベル付き直積を作るジャンクション。要するに複数本のワイヤーを一本にまとめる絵。まとめ方が、直積とラベル付き直積がある。ラベル付き直積は、「×」じゃなくてテンソル積風の「(×)」にした。同様にラベル付き直和は「(+)」。
- ラベル付き直和(ユニオン)の分解は、ジョインにあわせて丸印を付ければ良かった。そうでないと、ラベル付き直和構成を左右逆にしただけで区別が付きにくい気がする。
次の双対性がある。
ジャンクションの図の右側のほうには、等式的な型付け規則(typing rules)を書いている。データフローグラフ上での型付けとは、ワイヤーに対して「型で辺ラベルを付ける」こと。等式的な型付けでは、一本のワイヤーにひとつの型が付く。
一番単純なジャンクションを描き忘れた。それは単なるワイヤー。
ストレートジャンクション:
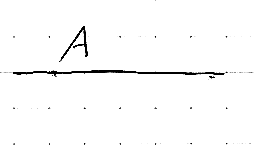
それと、ジャンクションとは違うが、射のクリーネスターがある。List関手と言っても同じ。f:A→B に対してクリーネスターを作用させると、f*:A*→B* となる。
クリーネスター関手:
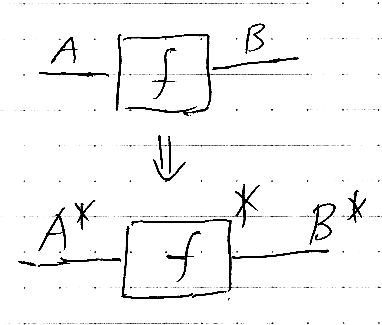
記号的な型付けのルールは次のようになる。
- fが基本コマンドなら、Dom[f] = dom(f), Cod[f] = cod(f)
- Dom[<F, G>] = Dom[F]∩Dom[G] , Cod[<F, G>] = Cod[F]×Cod[G]
- Dom[{F >:α, G >:β}] = Dom[F]∩Dom[G] , Cod[{F >:α, G >:β}] = Cod[F]α(×)Cod[G]β
- Dom[(α=> F, β=> G)] = α・Dom[F](+)β・Dom[G] , Cod[(α=> F, β=> G)] = Dom[F]∪Dom[G]
下付きの Aα は、プロパティ名がαのプロパティを表す。1つのプロパティは、そのプロパティだけを持つオブジェクトと同一視できるから、Aα は単一プロパティのオブジェクト型と思ってよい。すると、(×) は排他的マージ「++」となる。ナカグロで書いた α・A は、タグαを持つタグ付きデータ型。
等式的な型付けのルールなら次を使う。
だが、Catyは不等式的な型付けをするので、パイプラインの両端以外ではこのルールは適用しない。(暫定値を求めるのに使うことはある。)