In-Outコンポネントとパイプライン
http://d.hatena.ne.jp/m-hiyama/20071226/1198629573
年末年始にたいした予定があるわけでもないので、そこらでゴニョゴニョしているかもしれません。
ゴニョゴニュしている。まー、早寝しちゃうんで時間が取れないのだが、、、
In-Outコンポネント図
絵の描き方を考えた。まずは絵:
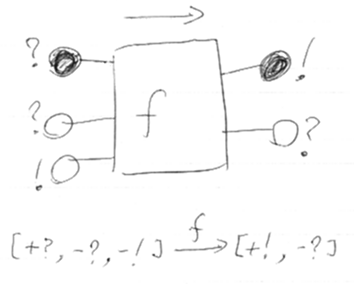
これは、Janusのコンポネントの特殊なもの。少し説明しておく; 箱fは射、射の向きは左から右。対象は、InとOutという記号(その実体はインターフェース)から生成される荷電自由モノイド(charged free monoid)であり、モノイド積がモノイド圏構造を与える。荷電(charged)は、偏極(polarized)とか符号付き(signed)といってもよい。要するに+, -が付くこと。
今回の絵ではプラスが黒丸、マイナスが白丸にした。絵記号をまとめると:
| 絵記号 | 意味 | 呼び名など |
|---|---|---|
| 疑問符'?' | 指標In | in, input, receive |
| 感嘆符'!' | 指標Out | out, output, send |
| 黒丸 | 符号+ | provide, call-in |
| 白丸 | 符号- | require, use, call-out |
| 棒(ロリポップ) | ポート | |
| 箱 | 射 |
アルファベット{?, !}に電荷を与えた荷電アルファベット(偏極アルファベット){+?, -?, +!, -!}上の列を [+?, -?, -!]のように書いて、この列をdomain/codomainの表現に使う。[]がモノイド単位、並置がモノイド積になる。荷電反転は単に+と-の入れ替え。
箱fの左側のポート列をarity(f)、右側のポート列をcoarity(f)とする。dom/codはarity/coarityと少し違って、
- dom(f) = arity(f)*
- cod(f) = coarity(f)
となる。上付き星は荷電反転。
ジャンクション(Id, σとか)を導入して、図形の操作に適当な同値関係を入れるとコンパクト閉圏になる。状態遷移系で意味を与えることもできる(だろう)。今回は深入りしない。
伝統的なフィルターなど
コンポネントのなかでプロファイルが [-?]→[-!] (require in; require out) であるものは伝統的なフィルターになる。その他に、[ ]→[+?] (none; provide in) が入力ファイル、[+!]→[ ] (provide out; none) が出力ファイル、[+!]→[+?] がパイプとなる。
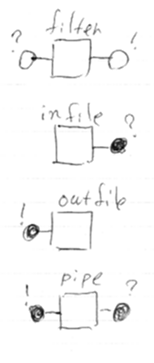
パイプをpとして、フィルターf, gに対して f|g = f;p;g としてフィルターの圏が作れる。この圏はモノイダルでもないし、荷電もない。つまらん。
古典的フィルターの拡張として、arityがすべて'?'記号、coarityがすべて'!'記号からなる射を考えて、これを一般化フィルターと呼ぶ。
一般化フィルターの全体は圏となり、モノイド構造が入る。が、射の双対(ベント・ジャンクション)をうまく定義できないからコンパクト閉にはならない。
パイプ結合演算とモノイド・プレ圏
一般化フィルターに対して、cod(f) = dom(g) でなくても、ポートの本数が等しいとき、パイプ結合が定義できる。
- 圏の意味で結合可能ならそのまま結合
- -?と-! はパイプを挿入して結合。
- +?と+! はポンプ(コピーフィルター)を挿入して結合。
- その他は結合不可能とする。
こうすると、一般化フィルターの全体は、dom, codをポート本数(自然数)として圏モドキとなる。cod(f) = dom(g)でもf|gが定義できないときもあるし、明白な恒等もない。が、同値関係を入れれば、パイプやポンプが恒等を表すし、結合律もOK。ただし、結合できない事態は残るから、対象が自然数である対称モノイド・プレ圏(symmetric monoidal precategory)となる。