ベル状態を使ったラムダ計算

アブラムスキー／クックの用語でいうベル状態／ベル余状態だけど、あれは確かに重要だよな。だって、コンパクト閉圏でラムダ計算しようとしたら必須の構成要素だもの。普通は、ベル・ナントカとかいわずに単位／余単位だけど。

このことは、お絵描きすれば実に明らか。

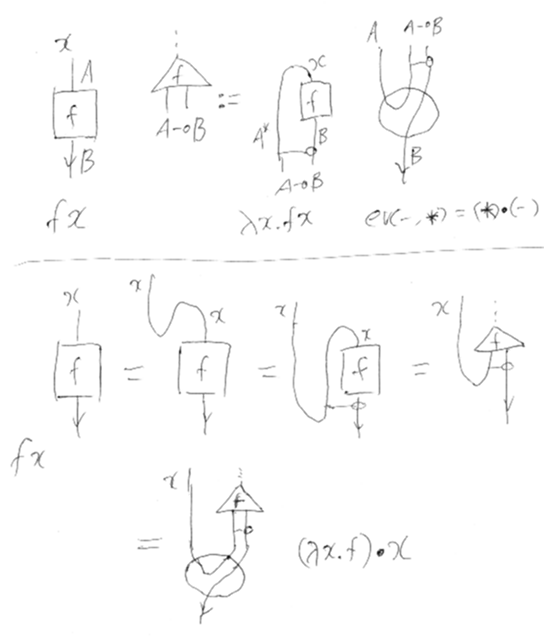
いちおう説明：

上段が定義、下段が計算。図示の方向は上から下（下から上じゃないよ！）。eval（計算科学ではむしろapply）はオダンゴ（ジョン・バエズは「evバブル」と呼ぶ）。指数 A -o B は双対とテンソル積で A^*×B と書ける。ev(x, f) = f・x なこと（位置の逆転）に注意。基本は普通のラムダ絵算と同じ。

この絵でいいたいことは fx = (λx.(fx))・x ってこと。エータ（イータ）変換と簡単なベータ変換を含んでいる。ｆのラムダ抽象はアブラムスキー／クックの三角で示したが、これはベル状態によるfのエンコード（アブラムスキーはfのnameとかconameと呼ぶ）。

計算のミソは、ベル状態とベル余状態でジグザグ等式が成立すること。空間的に離れたところでは過去と未来をズラしていいこと。空間的な隔たりは無視していいこと。

空間的な隔たりを考えると、これは量子テレポーテーションの絵になっている。つまりは、量子テレポーテーションとはベータ変換てことで、ベル状態とベル余状態がベータ変換を引き起こすメカニズムを与える。ウム、そうか。