このブログは、旧・はてなダイアリー「檜山正幸のキマイラ飼育記 メモ編」（http://d.hatena.ne.jp/m-hiyama-memo/）のデータを移行・保存したものであり、今後（2019年1月以降）更新の予定はありません。

今後の更新は、新しいブログ http://m-hiyama-memo.hatenablog.com/ で行います。

お絵描きはやっぱり楽しい

雑感 お絵描き 課題

ここ2日ほど、子供に「変な落書きばっかりしてる」とか言われながら絵算をしていた。

絵算はしばらくしないとできなくなる。が、勘が戻ると非常に楽しい。いきなりだと複雑そうにみえる和スター公式 (a + b)* = (a*b)*a* とかも自明に思えてくる。

できれば今日中に絵をスキャンして説明を付けよう。それが課題。[追記]課題はなんとか完了。[/追記]

基本変形：角度変形、アンワインド、スライディング、回転

お絵描き

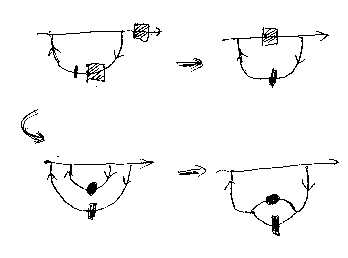
角度変形

まずは、3本以上の線（ワイヤー）が1点で交わっているときにその角度を変える変形。（ウギャ、上の段の左、矢印が間違っているがね、いいや、脳内修正して！）

なんでもないようだが、平面上に自由に描かれた構文図を双デカルト圏で解釈するときなどに必要。3本の線はΔや∇になっている。例えば次の3つの図は、黒丸をfだとして、f+ = Tr[∇;f;Δ] を表現している。

線4本以上が1点で交わっているとき、それをΔと∇で表現するときも、角度の変形を行って見やすくする。

アンワインド

次は、巻き付いたワイヤーをほどく操作。

箱の回りに時計回りまたは反時計回りにワイヤーが巻き付いているとき、この巻き糸をほどくことをアンワインドと呼ぶことにする。交差（クロス）を3次元的にブレイドと考えれば、交差の上側を引っ張り上げて回転させればほどける。

2次元内で変形するときは、箱を交差（クロス、対称）スライディングで動かして、残った巻いてる輪をヤンキングで解消する。

ループスライディング

次の図は、単にトレース付き圏のスライディングである。

ただし、黒丸（fとする）がループの中央に位置する絵はトレース付き圏では合理化できない。コンパクト閉圏ではじめて意味を持つ。しかし、計算がトレース付き圏で行われていても、便宜上、ループ中央にfを置くとなにかと便利。必要になった時点で、左または右までスライドさせればいい。

上下または左右の回転

3次元的な回転を使ってもよい状況がある。

上下の回転は、対称性／可換性があるときに使える。左右の回転は、ループに沿ったスライディング、交差に沿ったスライディング、それとタイトニングで合理化できる。

練習問題：2種類のスターの同値性

お絵描き 計算 具体例

f*には、次の2つの代表的表現がある。

  1. Tr[(1+Δ);(σ + f);(1 + ∇)]
  2. Tr[(1+f);∇;Δ]

参考：

この2つが同値であることを示してみる。


  1. まず、左右の回転で交差を解消する。
  2. 角度変形で全体の形を整える。
  3. 上下の回転でfと1を入れ替える。
  4. 角度変形で全体の形を整える。

実は、回転を使わないほうが計算は楽。


  1. 右の∇をループに沿ってスライディングする。
  2. ループの外側のワイヤーはアンワインドできるので、ほどく。
  3. もし必要なら、fもループに沿ってスライディングする。

年末年始で考えたこと：記号回路とか両側半加群とか - 檜山正幸のキマイラ飼育記 メモ編（http://d.hatena.ne.jp/m-hiyama-memo/20080104/1199433463）より引用：

トレース付き圏で、3次元的な回転を使った変形で計算できることがわかった。この計算は、コンパクト閉圏なら合理化できるがトレース付き圏だけだと合理化できない。それに、実は計算が簡単になるわけでもなく、むしろ計算過程が増えたりする。

それにもかかわらず、この計算法は直感的で面白い。計算の途中で現れる図形が珍しかったりして発見的な意味もある。

f* = 1∨f+ の計算

お絵描き 計算 具体例

背景は次を参照：

f*の定義は、Tr[(1+Δ);(σ + f);(1 + ∇)] で与えるとする。これが、Tr[(1+f);∇;Δ] と同じであることは既に示した。f∨g = Δ;(f+g);∇、f+ = Tr[∇;f;Δ] として、f* = 1∨f+ の計算は意外に面倒。

左右、上下の回転を使って示してみる。

双代数法則とは、∇;Δ = □ という法則。これについては後で詳述する。この双代数法則以外は、角度の変形と左右回転（交差ねじれの解消）と上下回転（和の可換律）だけしか使ってない。

双代数法則の後は、右下の∇をループに沿ってスライディングして、巻いているワイヤーをほどいたほうが計算は速い。

積スター公式と和スター公式

お絵描き 計算 具体例

コンウェイ半環（Conway半環）で次が成立する。

  1. (ab)* = 1 + a(ba)*b
  2. (a + b)* = (b + a)* = (a*b)*a*

これをトレース付き双デカルト圏に持ってくると、

  1. (f;g)* = 1 + f;(g;f)*;g
  2. (f∨g)* = (g∨f)* = (f*;g)*;f*

これらを示す。まずは積スター公式：fが黒丸、gが黒四角とする。

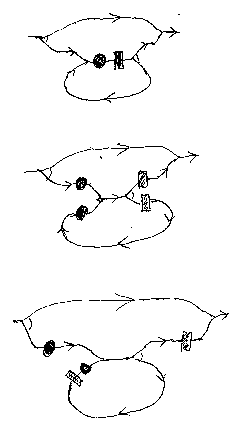
スターの定義としては 1∨f+を採用する。f* = 1∨f+ の計算でむずかしい部分は既に終わっている。∇、Δに沿ってコピースライディング（重複化）して、その後右下のgをループに沿ってスライディングする。ワイヤーの長さをタイトニングとシフトで調整しておしまい。


次は和スター公式：


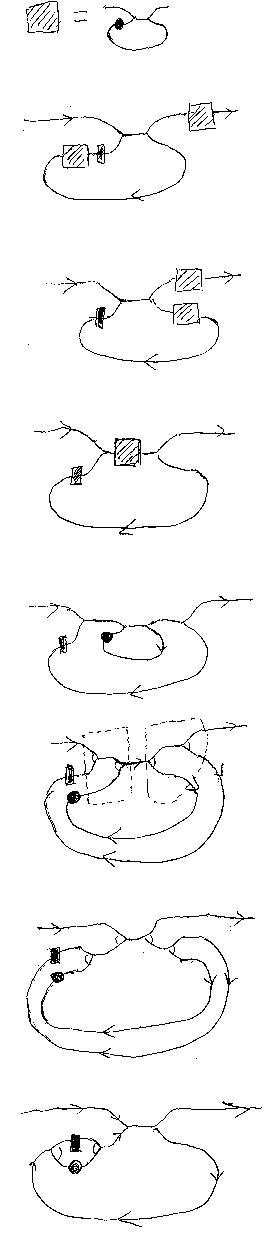
  1. f* = Tr[(1+f)∇;Δ] を箱（xとする）に入れておく。
  2. (f*;g)*;f* = (x;g)*;x からスタート。
  3. 左のxをループに沿ってスライディング。
  4. コピースライディングの逆でxを1つにまとめる。
  5. 箱xを開く。
  6. 加法∇と対角Δの結合律。
  7. 左下のΔをループに沿ってスライディング。
  8. (g∨f)* = (f∨g)*の出来上がり。

図の描き方によってはもっと簡単になる、それは後述する。

双代数法則

お絵描き 圏一般論 その他代数

双代数法則（双代数条件）とは、1つの圏にデカルト構造、余デカルト構造が載っているとき、それらが協調していることを示す条件である。∇;Δ = □ という等式で示せる。

双代数法則は、対角Δがモノイド射（加法的）であること、また、加法∇がコモノイド射（余加法的）であることを主張している。このことは、行列の絵算で容易に確認できる。

双代数法則を絵算で使うとき、位相的同位変形ではなくて、ある領域（チャンバー、ボックス）を置換することになる。これは2次元で計算（絵の変形）しているせいで、3次元なら特異点を通る変形、4次元ならおそらく特異性が表れない変形となるだろう。

絵算の外部空間（背景）の次元が低いと、同値変形で特異性が出現する。加法の交換法則やヤンキングを2次元内で遂行しようとすると、特異性が避けられない。

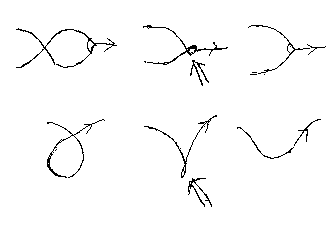
3次元を使って変形すれば、特異性は出ないが、2次元では変形の途中で捻れやシコリ、ダマを無理に潰すことになる。

さて、双代数法則を3次元内で表現すると次のようになる。

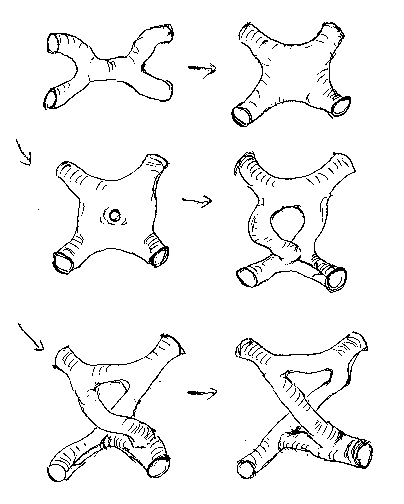
4つの穴が開いた球面が、4つの穴が開いたトーラスに変わる瞬間がある。そこが変形の特異点になっている。その他は連続変形である。

結合律の表現とより簡便な絵算

お絵描き

加法∇の結合律、対角Δの余結合律は次の形にも図示できる。

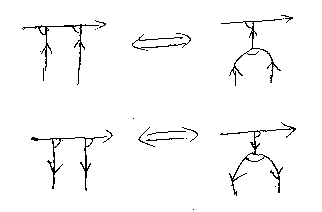
この図示方式で次が示せる。

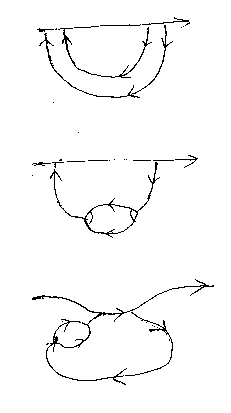
これはトレースの2回繰り返しからΔ;∇という小さな穴（川の中州; hole, sandbar）が生じることを示している。加法がベキ等なら、Δ;∇ = 1 なので穴は消える。図の横線の中央にfを置けば、ベキ等圏における(f+)+ = f+ が得られる。

この結合律の図式法は、和スター公式の証明にも効果的に使える。影のかかった箱x、黒丸f、黒四角gの意味は前のエントリーと同じとして、和スター公式は次のように短く示せる。