型定義も制約述語もインスタンスも問い合わせも区別する必然性はない
ということを、またしてもスピヴァックから教わった。
最近、gv:draw-data というコマンドを作ったのだが、データ(XJSONインスタンス)をグラフに描く。例えば、[@userNum 123, , "hello"] だと、次のようになる。
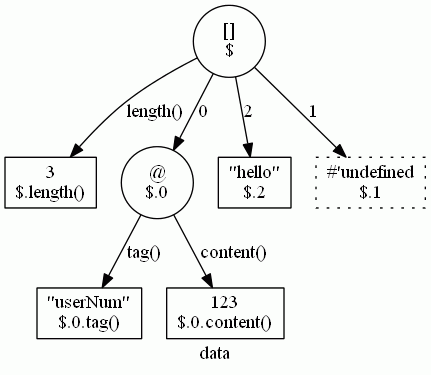
もっと簡単な {"x":2, "y":2} だと次。
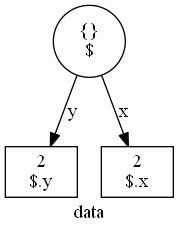
gv:draw-dataは常にツリーを描くが、この例では値2が共有されているので、辺xと辺yを合流させてもいいい。
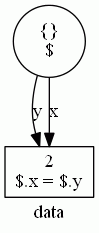
普通はインスタンスをツリーに描くが、合流があってもいいので、一般的にはインスタンスのグラフはDAGとなる。ただし、インスタンスはサイクルは含まない(スキーマのグラフはサイクリックになる、再帰的定義があるから)。
さて、次の図は、{"x": integer, "y": integer} というスキーマの図だ。
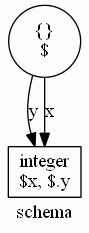
I = {"x":2, "y":3} 、S = {"x": integer, "y": integer} と置く。インスタンスIをスキーマSでバリデーションするとは、まずは次のような関手を作ることになる。
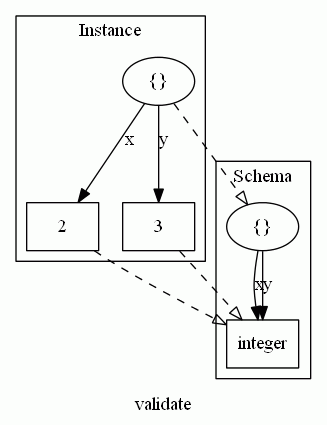
破線矢印が関手による対応。スキーマ側の末端ノードはintegerだが、これを関手の逆方向に沿って引き戻す。すると、インスタンスの2つの末端ノードにintegerが(逆方向に)運ばれて乗っかる。もともとあった定数 2, 3 と 型 integer を比較すると、
- 2∈integer
- 3∈integer
となるので、バリデーションが成功する。インスタンスをスキーマとみなせば、末端には整数のシングルトン型があるので、
- {2}⊆integer
- {3}⊆integer
という包含性による比較となる。
インスタンスもスキーマもグラフ=圏であり、バリデーションとは関手の構成と末端ノードでの比較であることがわかる(グロタンディーク構成した圏における射の存在)。問い合わせの議論も同様に関手の構成として理解できる。
"It's all categories and functors!" とはこういうことだ。