f.α という記法とホモトピー

本編でも書いたDOTNの話。

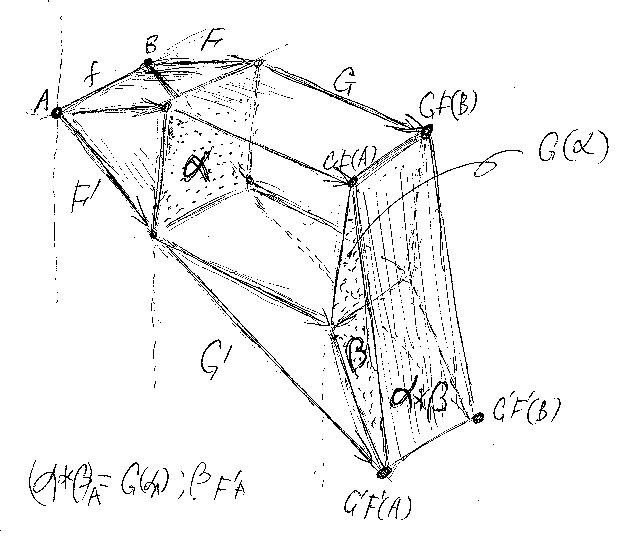
F, G:C→D で f:a→b in C だとする。α::F⇒ G:C→D があるとして、f.F, f.G, a.α, b.α を4辺とする可換四角形ができる。この四角形を f.α と書くことにする。f.αは、D^→という関手圏の射として意味を持つ。f.α:f.F→f.G in D^→ となる。

さて、H:D→E があると、Hは、D^→→E^→ まで持ち上げることができる。可換四角形のすべての辺にHを適用して写せばいい。これは H^→ と書けるが、HとH^→ をオーバーロードする。

可換四角形 f.α のH（ほんとはH^→）による像を (f.α).H = f.α.H と書く。β::H⇒K:D→E に対する (f.K).β も可換四角形だが、(f.α).H と (f.K).β は縦結合可能なので、(f.α.H);(f.K.β) in E^→ が作れる。これが、f.(α*β) を与える。つまり、自然変換は、射に可換四角形を対応付けるルールとみなせる。四角形を2セルとみたときの始辺と終辺が関手F, Gで与えられる。C→D の関手に働く自然変換は、C→D^→ の関手のように思える。

これは、Catのデカルト閉性から次を意味する。

• Cat(C, D^→) = Cat(C×→, D)

C×→ は柱体なので、自然変換は、空間Cと空間Dの間の写像（関手）の離散的ホモトピーを与える。

ウーム、やっぱりホモトピーか。