山勘がまた当たった、好調、それにしても
モナドの計算でヤン・バクスター方程式(=ライデマイスター移動のIII番)が出て来るだろうとは、なんとなく予想はしていた。だが、えらくアッサリとご登場。あまりにもアッサリ、なにげに登場したので、僕はかえって出会い頭でビックリしてしまった。
やっぱりそうかぁーーー、という思いはあるんだが、なんつうか、不気味というか、なにかの因縁/必然性を感じてプチ感動というか、、、不思議に複雑な気分だわ。
事情は、それほど難しい話じゃないけど忘れるに決まっているから、これに関しては近々丁寧に書くつもりだ。
写真を撮ってあるので、それを提示して今ザックリとしたメモを書いておこう。
次↓は、スターバックスのナプキン。一度丸めて捨てようとしたのだが、記念(?)にしようと持って帰った(写真を撮った後に捨てたが)。

実際はモナドの計算なんだが、線形代数的な用語で言うと:多元環A上の左加群Mがあるとき、逆転(opposite)乗法を持つ多元環Aop上の右加群を構成する話。さまざまなスワップ(ツイストと呼びたい人もいる)と、スワップに関して演算がすり抜け(pass-through)できるという法則が登場する(公理や定理として)。その法則のなかに、次↓のような形のものがある(ナプキンの一部)。
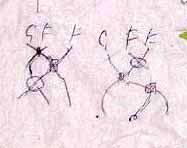
これはヤン・バクスター方程式に他ならない。普通の結び目の場合とは違い、スワッパー(交差)が2種類ある。絵ではシルシで区別しているが分かりにくい。この「種類」はブレイドの正負(奥行き)とはまったく違う。ほんとに2種類:F-F交差とG-F交差。2種類の交差も含めてのヤン・バクスター型の等式となっている。
ノートに書き写したのが次↓。Fの逆転乗法○とFの右からの作用(スカラー乗法)* を定義している。多元環の乗法○と、右スカラー乗法 * に関して結合律を証明したい、という状況。紙面一番下の絵図等式が示すべき等式だ。
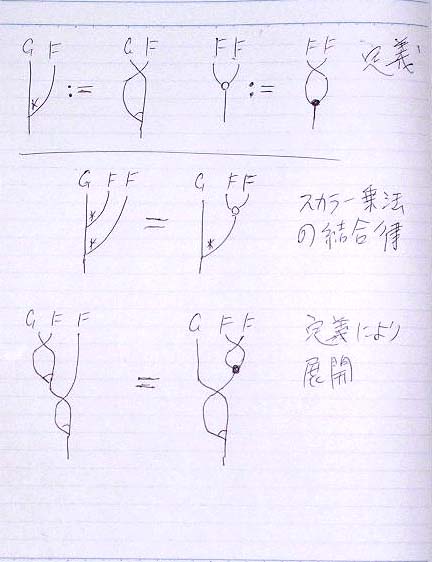
すり抜け法則を使って変形すると、図の下半分は一致する。結合法則の等式を示すためには、上半分の等しさがあればいいのだが、これがヤン・バクスター型の方程式となっている(紙面の右側に縦に等式が書いてある)。
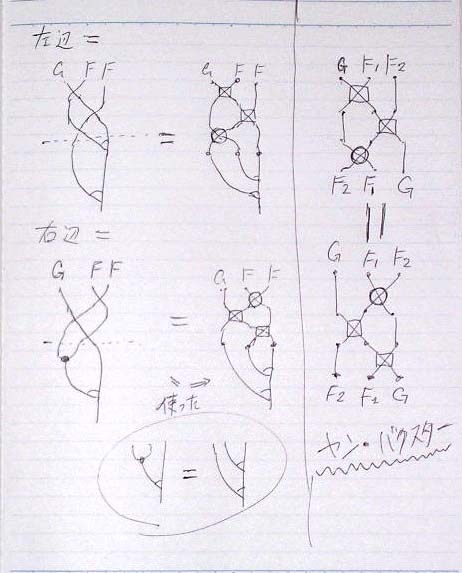
つまり、スワップの基本公式(僕は、バニッシング法則とバンドル/アンバンドル法則(バンドリング/アンバンドリング法則)と名付けた;いつか書く)といくつかのすり抜け(pass through)法則、それとヤン・バクスター型の等式(ライデマイスター移動IIIの類似)があると、左加群から右加群を構成できる。この左から右(あるいは右から左)は、構造のスワップ(ミラー・イメージ)とも言える。
なんで「左から右」(あるいは「右から左」)へのスワップが必要かというと、モナド上の加群(作用)をベースにしてクライスリ構成(の類似)をやろうと思うと、スワップなしではできないからだ。
ベックの分配法則による複合モナドの構成、モッギモッジのテンソル強度(tensorial strength)によるCirc-Kleisli構成、コモナド・モナド対からの両クライスリ構成など、すべて同じ方法を使っている。スワッパー(分配法則、テンソル強度)を使ってクライスリ結合を定義している。
2006年1月「ソースコードの形式化」でCirc-Kleisli構成に言及している(もっと前から意識していたと思う)。2006年5月に「懸案のCirc-Kleisli構成をやっと確認できた。」と書いている。Circ-Klisli構成を作るには、何ヶ月もかかった。しかも、テンソル強度に関しては納得感がないままに計算していた。テキストに書き下す方法も持っていなかった(絵だけ)。
両クライスリ構成(diKleisli構成、biKleisliという言葉が既にあるけど)は、思いついた翌日に計算は終わった(「両クライスリ圏が構成できた」)。
モナド上の加群に関しては、30分程度で確認できた。オマケとしてヤン・バクスター方程式が付いてきた。絵算とDOTNに関してちっとは上達したってことかな。
「次の計算」で書いたように、
この作業が(膨大に)残っている。なにをやっても許される、天国のような計算体系があるに違いない。