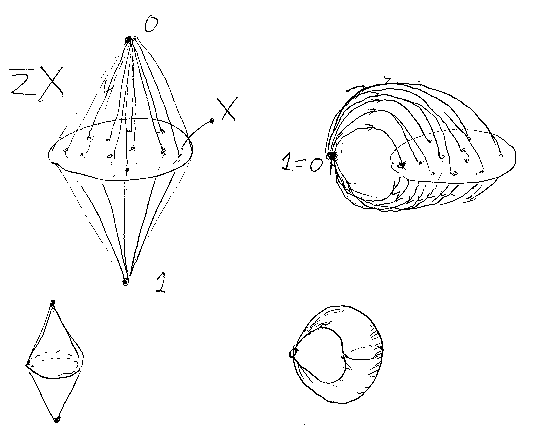
断面と懸垂

うーん、手首の状態が酷い。キーボードも辛いが、手書きが壊滅的だし。ハァー。
それはそうと；
昨日の晩、布団のなかで思いついた。

まず、圏のホムセットの絵を描く。

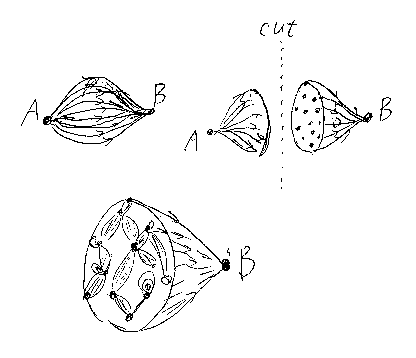
射を矢印（線）で描くと、なんか筋繊維がむき出しのカエルの足みたいになる。これをまんなかへん(?)でスパッと切ると、断面は（離散的な）点集合に見える。もし、もとの圏が2-圏／双圏であれば、この断面に圏が現れる。

以上の状況の逆を考える。点集合Xに対して、懸垂を作る。ただし、0から1への向きを付ける。と、矢印の束ができるから、これで点集合から射集合ができる。0と1を同一視すると、約懸垂というヤツだが、これでループ集合ができる。モノイド圏を単対象の双圏とみなすのは、この約懸垂を作る操作だ。