ライデマイスター、トゥラエフ、マルコフの移動
カウフマン(Kauffman;http://www.math.uic.edu/~kauffman/)の本(結び目の数学と物理)と小島さんの本(講座 数学の考え方〈22〉3次元の幾何学)をもとにして記述する。カウフマンP.11と、小島P.148, 149の図を比較する。
まず、トゥラエフ移動はライデマイスター移動を完全に含むことに注意。通常、ライデマイスター移動は、I, II, IIIと番号が付けられるが、カウフマンは移動0を加えている。トゥラエフ移動は3次元タングルを2次元に射影した図(タングル図)に関するもの、ライデマイスター移動は結び目の射影図に関するものだが、事情はよく似ている。
小島本の図からわかるように、トゥラエフ固有の移動は、一般のモノイド圏で成立する縦スライド(トレース付きモノイド圏の公理に「スライディング」があるので、用語「シフト」が適切だろう)、交差と極大点の交換、ジグザグ公式。ジグザグ公式はライデマイスター移動0だから、実際は交差(クロッシング)と極大点(ベント、ターニング)の交換だけが、トゥラエフ固有の移動である。
一応、トゥラエフ移動を列挙してみる。σとσ'は符号が逆な交差(クロッシング)である。
- id;f = f, f;id = f に対応する2つの縦スライド
- (f + id);(id + g) = (id + f);(g + id)に対応する縦スライド
- ジグザグ公式に対応する2つの移動(ライデマイスター移動0)
- (1 + ε);(σ + 1) = (ε + 1);(1 + σ')、(1 + ε);(σ' + 1) = (ε + 1);(1 + σ) に対応するトゥラエフ固有の移動。
- ライデマイスター移動I -- ヤンキング
- ライデマイスター移動II -- σσ' = 1 (ブレイドの逆元)
- ライデマイスター移動III -- アルチンのブレイド関係式
トゥラエフに固有の移動は、「⊂」形のマンナカ(極点)を直線を貫いた形をどのように表現するか、それらの表現バリアントが等しいことを示す。(次の図)
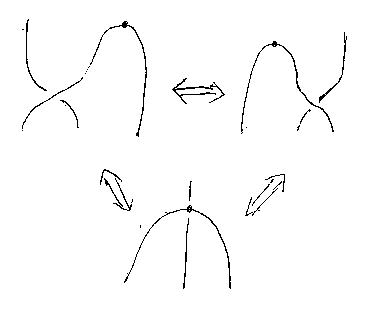
ライデマイスター移動IIは、90度回転して(?)見ると、重なった(だが、からんでない)「⊃」と「⊂」を引き離す移動にも見える。2つのクロスと重なった(からむ、からまない)ベントは同じとはこういうことか。(左右の親指人差し指で実験できる。)
以下は、特異点(尖点、二重接点、三重点)と関連させたライデマイスター移動の図。
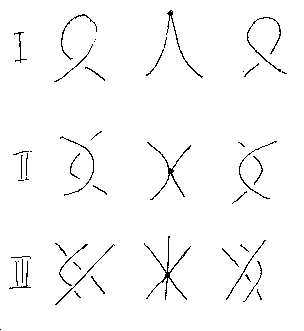
次はマルコフ移動。
マルコフ(Markov)は、ブレイド閉包を考察したわけだが、閉包をとって同じからみ目になるブレイドがどんな関係かをみる。つまり、Cl(b) = Cl(b')なとき、bとb'にはどんな関係があるか?
- bとx'bxは閉包が同じになる。x'はxの逆元。
- bと(b + 1);((n-1) + σ)は閉包が同じになる。σは交差。
1番目は、トレースのスライディングを使えば明らか。2番目はタイトニングしてからヤンキングすればわかる。つまり、トレース付きモノイド圏の公理から出る。
マルコフ移動は、ブレイド圏における同値関係を生成する基本関係式だと捉えてよい。