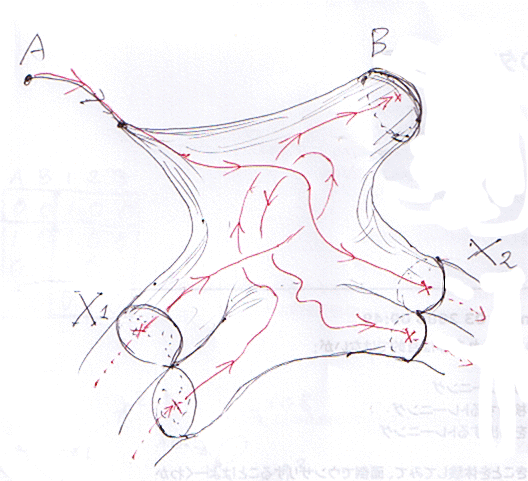
圏のトレース（ルーピング）

繰り返しだが； 重み／ラベル付き二部グラフと半環係数の行列は同じものだと考えていい。二部グラフの両端を重ねてグラフやオートマトンが作れる。もとの正方行列は隣接行列や遷移行列に他ならない。始状態は入射行列、終状態は射影行列で表現される。入射I、遷移S、射影Pの組(I, S, P)でオーマトンを表現すると、振る舞いはI;S*;P = PS*I となる（「;」は図式順結合）。絵で描くと：

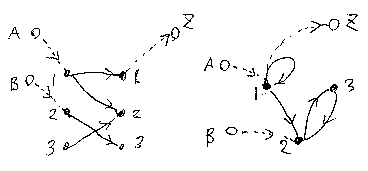
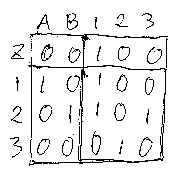
(I, S, P)と(J, T, Q)があるとき、これらの結合を直接的に書き下すには、直和S+Tとトレース記法を使う必要がある。だが、振る舞いはI;S*;P;J;T*;Qで与えられるので、非常に単純化される。これが振る舞いを考える大きな理由だろう。

構文図式、オートマトンの例を山勘で一般化すると、こんな感じ：

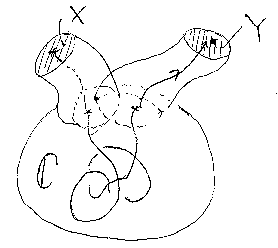
入り口Xから入った経路は、圏Cのなかを走ってから出口Yに至る。境界付き圏。

特殊ケースとして、ウエス・アタッチメントがある：

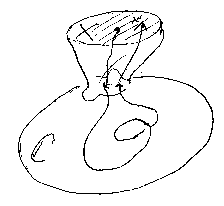
変数集合Vの有限集合の全体Xが入り口であり出口である。変数を含んで変数に出力する式（射）を問題にすれば、出入り口（変数集合の集合）をウエス・アタッチメントして、そこをスタート・エンドとする射だけを考えることになる。実際には、出入り口に関してトレース（ルーピング）しているのだけど、出入り口断面を基点とする経路（射）だけを考える。アタッチしてトレースして、対象を断面に制限（部分圏を考える）している。

もっと一般的な状況：