リーズニングの比喩とまとめ方

比喩：

	具体素子	基本リーズニング	証明図（スチル）	ムービー
料理	食材	基本調理法	料理のスナップショット	料理動画
回路工作	素子とワイヤー	基本組み立て法	回路のスナップショット	工作動画
ピクチャーパズル	ピース	基本組み立て法	ピクチャーのスナップショット	実況動画

1. NKは、料理を1枚のレシピで伝える方式、出来上がり写真〈スチル〉が証明図
2. LKは、料理動画〈ムービー〉で伝える方式

まとめ方は、論理記号8つの導入と除去で表を作るのがよい。ただし、我々は否定を組み込み扱いしないので7つに減る。（一般的に論理記号を減らすことは練習問題。）

• 導入： ↓→証明図の下端に新たに、論理記号が入った論理式を追加すること。それに伴い証明図全体の書き換えが起きる。
• 除去： ↓→証明図の既にある論理記号が入った下端論理式の下に、その論理記号がない論理式を追加すること。それに伴い証明図全体の書き換えが起きる。論理式を取り去ることではない。

導入しても除去しても、証明図は書き換えられる（受動表現であり、可能表現にあらず、「られる」は要注意）。

記号	導入法	除去法
T	!素子の結合	絶対証明図の作成
⊥	背理法証明図の作成	θ素子の結合
∧	有限◇リーズニング	π素子の結合
∨	ι素子の結合	有限□リーズニング
∀	任意◇リーズニング	t:X→X×Y 具体例
∃	t:X→X×Y 具体例	任意□リーズニング
⇒	Λリーズニング	ε素子の結合

注意事項：

1. 否定は入ってない。¬A ≡ A⇒⊥ と定義する。
2. 二段ずつに区切って、たすきがけの双対性がある。合計6つの双対性。ただし双対性は対偶双対性とド・モルガン双対性があり。真横方向で左右の随伴性がある。双対性・随伴性の種類は違う。含意は双対の相手がいないで孤立している。
3. 素子も、{基本 | プリミティブ | 組み込み | ビルトイン}リーズニングも、システムには{総称 | パターン}で準備されているので、利用する前に総称パラメータ（命題変数、{型|ソート}変数）の具体化が必要。
4. 具体例とは、セクションが引き起こす反変作用（引き戻し）による対象の移動〈transfer | 転送 | 移送〉。
5. 最後の'⇒'の行は、Λリーズニング＝カリー化とε素子（MP、eval）の結合が随伴の転置と反転置になっている。
6. つまり、この表には、双対・随伴がギッチリと詰め込まれている。

他にケーブリング（ワイヤーとケーブルを扱う技術）とジャンクション（リーズニングの際に使う内部素子）が必要。

上記の !, θ, π, ι, ε 以外のジャンクション〈構造素子〉は：

1. id、恒等、自明
2. 同一分岐〈複製 | 対角 | duplication | diagonal | copy〉
3. 同一合流〈マージ | 余対角 | merge | codiagonal〉 中間領域がOR領域になることに注意。
4. {AND | 連言}合流： ケーブルの入り口とは違うが、しばしば混同される。
5. {{OR | 選言}{分岐 | 分解} | 場合分け}： 中間領域がOR領域になることに注意。
6. シャフル〈swap | permutation | symmetry | interchange | exchange〉

基本リーズニングは：

1. ; SeqComp, Comp, Cut、素子との結合、証明図どうしの結合、↓→なら縦に繋ぐ
2. ParComp, Tensor、↓→なら横に併置
3. ◇ Diamond, ?Tuple、∧-∀導入
4. □ Squre, ?Cotuple、∨-∃除去
5. Λ Lambda, Curry、⇒導入

これでOKだと思う。抜けていたら後で追記する。

[追記]

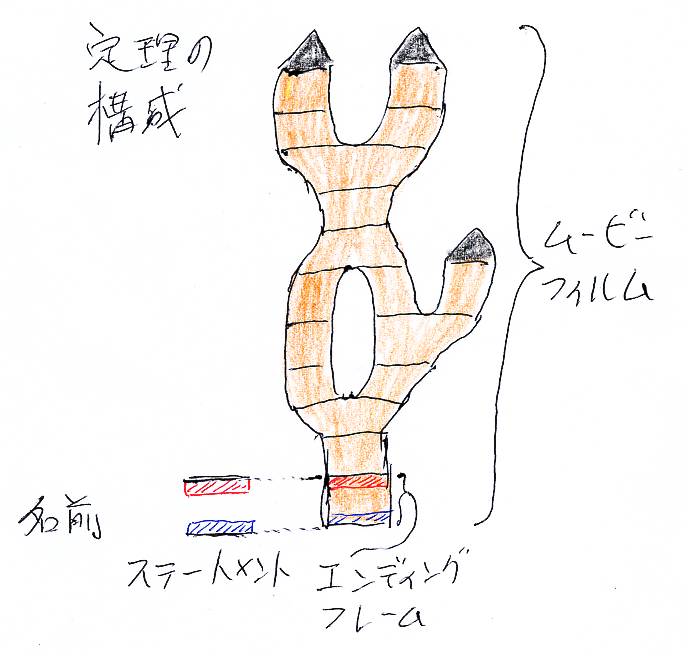
別な話題だが、ここにまとめて書いておこう。シーケント Γ → A がステートメントである場合と、証明図である場合を区別するために、証明図を表すシーケントを Γ-○→A のように書く。手書きのときは、→ に ○ を重ね書きする。

ステートメントのシーケントは、ほんとに論理式リストのペアであって中身が一切ない。証明図は中身があるので、その中身に名前を付けたり、式で表現するときは、

• Γ-(名前)→A
• Γ-(式)→A

のように書く。これで、ステートメントのシーケントと、証明図のシーケントを区別できるだろう。

[/追記]
[追記]

用語法の不適切さや不備に悩まされる時間が考える時間の8割くらいかな。フントニモウ。

定理（公理も含む）の記述形式。

	総称〈パターン〉形式	具体化形式
絶対形式	論理{公理・定理 | 法則 }	{論理的に}?恒真な命題
相対形式	推論規則	{論理的に}?正しい推論

論理的公理ではない分野固有公理は、具体化形式で与えられるので、総称の具体化メカニズム（命題変数への代入・置換）は使わないが、全称命題の具体化メカニズム（個体変数への代入・置換）を使う。変数の種類が違うだけで、どちらも代入・置換。

命題総称〈命題ジェネリックス〉と全称命題の区別も出来にくいかも。

• ∀A, B∈Prop.( T → A∧B⇒A ) これは命題総称を、命題変数を束縛した全称命題で書いた。
• ∀a, b∈R.( a≧0, b≧0 → a + b ≧0) 通常の全称命題

等式の推論規則は、論理的と分野固有の中間的なもので、分野固有の形（命題変数なし）でも書けるが、次の論理的推論規則があると格段に便利。

  P s = t
 --------- replace-equal<P, s, t>
  P[s←t]

ここで、Pは命題変数で、[s←t]は出現（セレクション、リデックス）を指定しての置換（むしろリプレースメント）。s, tは項変数なので、任意の項に置換可能。

これは、ひとつ命題Pと、等式命題 s = t を入力とするリーズニングだが、項変数とリプレースメントを使っているので非常に高度だ。

類似の規則に、

  P (A ⇔ B)
 ------------ replace-equiv<P, A, B>
  P[A←B]

これは、ひとつ命題Pと、同値命題〈双条件法命題〉 A ⇔ B を入力とするリーズニング。基本〈プリミティブ | 組み込み〉にする必要はないが、論理的推論〈リーズニング〉に関する定理〈メタ定理〉として、総称証明可能性〈マクロ規則の存在〉が{メタ}?証明できるはず。

こういったマクロ規則は、便利規則〈convenient rule〉として最初から演繹システムに入れてもいいだろう。規則とは、総称定理〈定理パターン〉だから、ユーザーによって導入された総称定理群〈シェマ〉だと思えばよい（シェマ変数 ＝ 命題変数または項変数）。

[/追記]