代数的複体の概念

圏Cに値を取る代数的複体という概念をCplx(C)と表すことにすると：

• Cが付点圏〈pointed category〉（零対象を持つ圏）であれば、Cplx(C)を定義できる。
• Cが加法圏でないと、複体のあいだのホモトピー同値関係を定義できない。
• Cがアーベル圏でないと、複体のホモロジー／コホモロジーをを定義できない。

通常は、ホモロジー／コホモロジーを定義したいので、Cはアーベル圏にとる。が、とりあえず付点圏の範囲でやれるところまでやるのは意味がある。Cは付点圏だとする。

まずは、Z∪{⊥} を対象とする圏を生成箙で定義する。

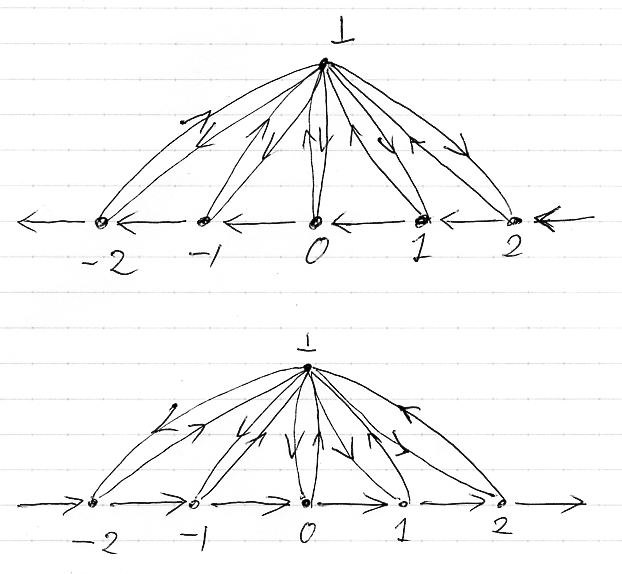
これは、互いに反対圏となっている2つの圏（の生成箙）。どっちかをΓとすると、もう一方がΓ^opとなる。仮に上のほうをΓとする。

付点圏の圏のホムセット（ホム圏ではない）をPtCat(C, D)とする。圏（2-圏ではない）PtCatで、指数 [C, D]が作れる。特にPtCatの指数だということを強調する意味で [C, D]_pt とも書く。

以上の設定のもとで、Γ∈|PtCat|、もちろん Γ^op∈|PtCat|。C∈|PtCat| に対して、[Γ, C]_pt, [Γ^op, C]_pt が再びPtCatに入る。PtCatは直和を持つので、次が作れる。

• [Γ, C]_pt[Γ^op, C]_pt

S:C^op→C は、S:C→C^op とも言えるので、S*S:C^op→C^op を作れて、さらに S*S:C→C とみなせる。よって次の自然変換ιに意味がある。

• ι::S*S⇒C^:C→C

ιが自然同型のとき、(S,ι)をC上の反対合〈anti-involution〉と呼ぶ（https://en.wikipedia.org/wiki/Involution_%28mathematics%29）。重要な事実は、

• Cが反対合を持つなら、[Γ, C]_pt[Γ^op, C]_pt にも反対合が入る（持ち上がる）。