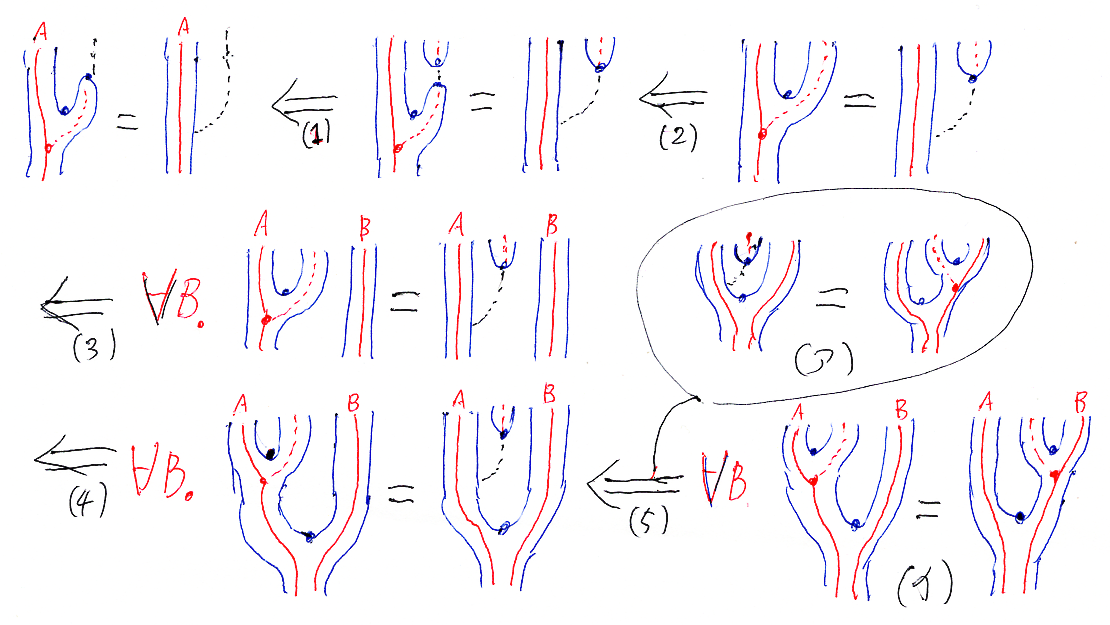モノイド圏の標準表現と単位対象
参考:
- モノイド圏の単位対象の定義について: これ難しいやん - 檜山正幸のキマイラ飼育記
- http://www.sciencedirect.com/science/article/pii/S0001870883710558
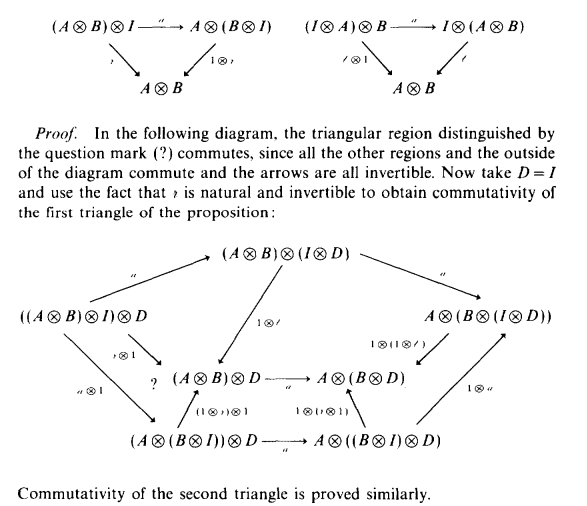
標準表現は右標準表現を考える。とりあえず絵だけ並べる。
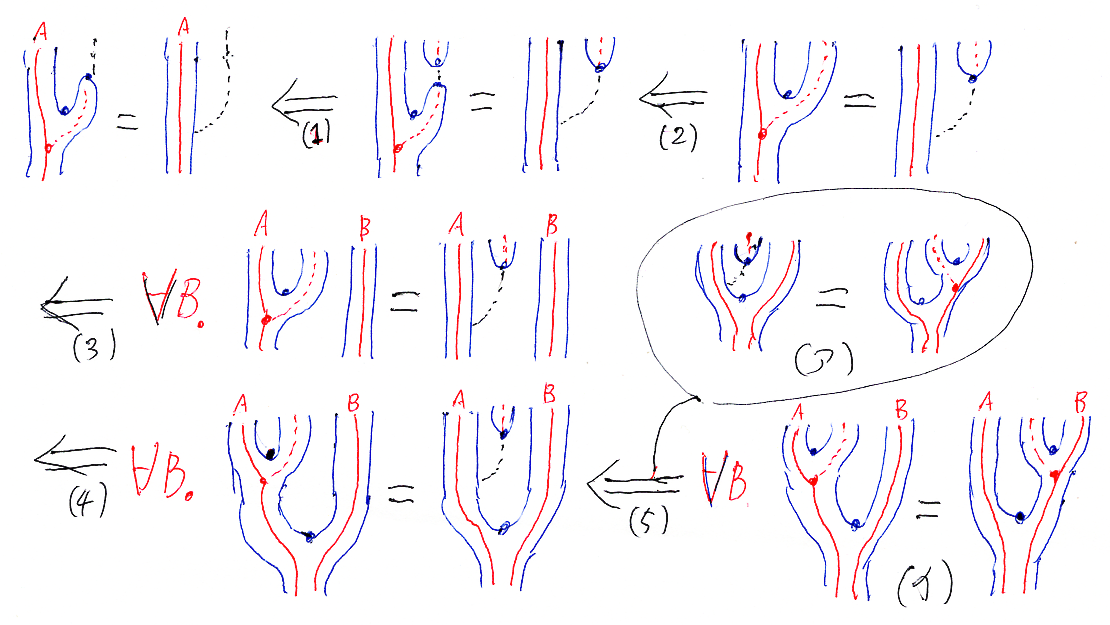
これはバックワード・リーズニングになっているので、最初が結論。補題(ア)と補題(イ)があって、それを使って結論を証明する。
最初に、図式の等式的リーズニングだが、次のような推論規則がある。
- 反射律(公理)
- 対象律(推論規則)
- 装飾律(推論規則)
- 置換律(推論規則)
装飾と置換は次のよう。
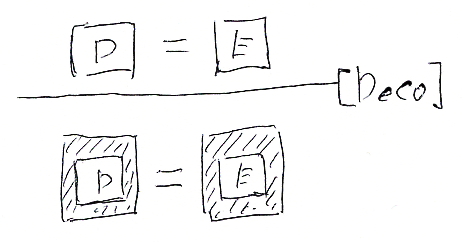
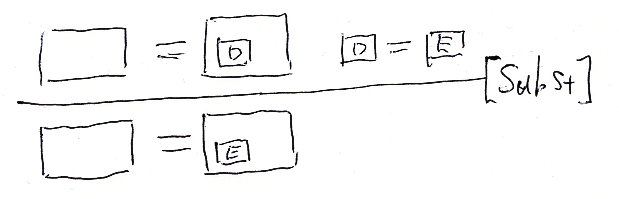
特殊な状況で成立する左右の消約律。
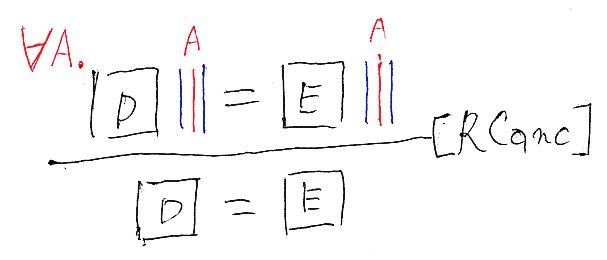
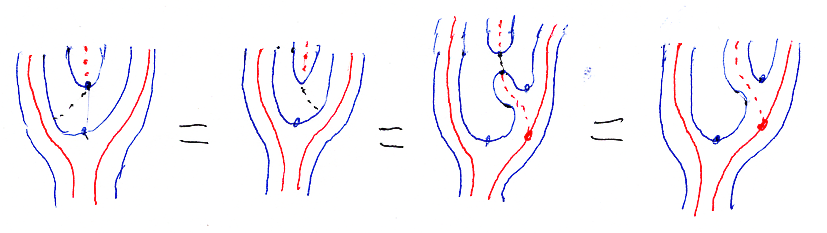
消約律は次のようにして証明(導出)できる。
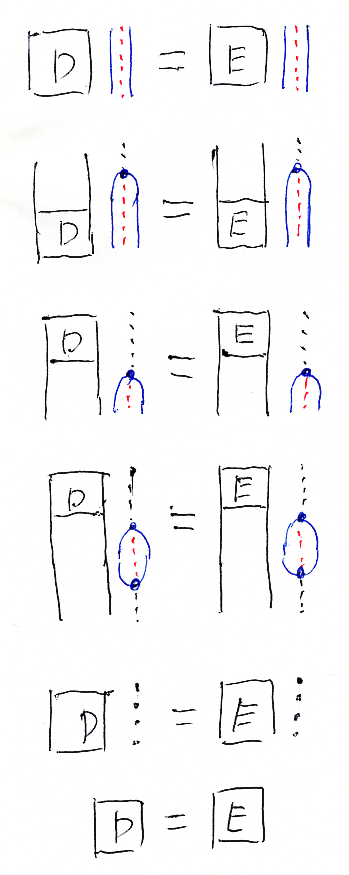
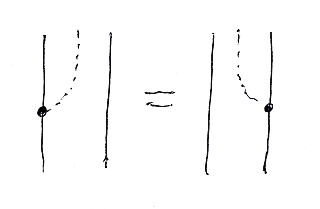
使う道具はストライプ図(ケーブル図)。右が略記。
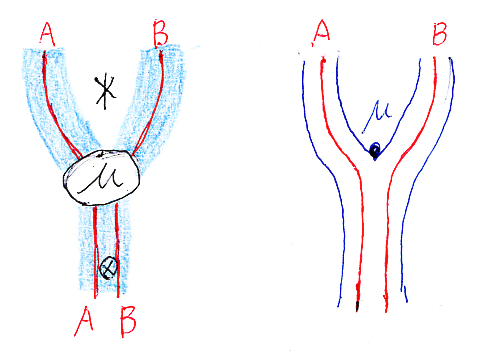
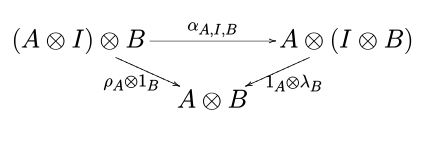
マックレーンの三角等式と、右表現の左単位律を仮定する。左単位律は三角等式と同値。
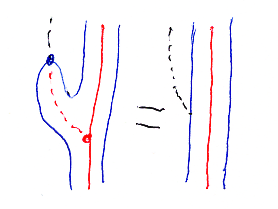
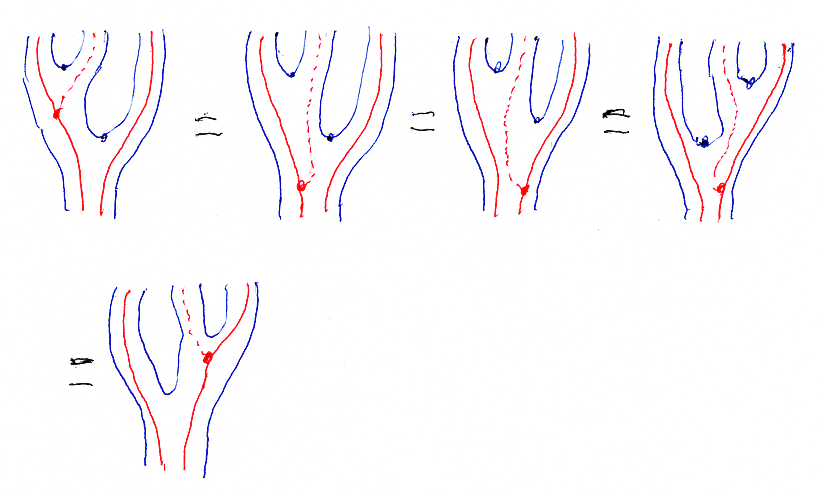
右表現がタイト・モノイド関手であることから、乗法と単位が可逆。
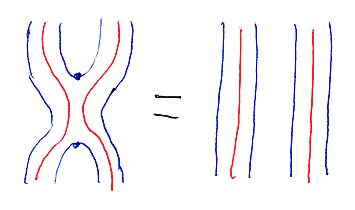
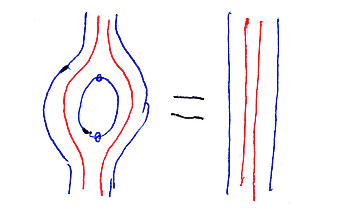
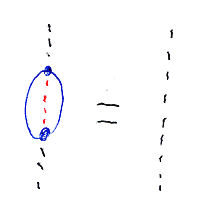
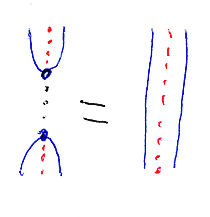
念のために、もう一度主証明。