このブログは、旧・はてなダイアリー「檜山正幸のキマイラ飼育記 メモ編」（http://d.hatena.ne.jp/m-hiyama-memo/）のデータを移行・保存したものであり、今後（2019年1月以降）更新の予定はありません。

今後の更新は、新しいブログ http://m-hiyama-memo.hatenablog.com/ で行います。

Poly(C)の構成の方法

多圏 モノイド圏 気付いた

やたっ、これでうまくいきそう。

Poly(C)の構成の方針 - 檜山正幸のキマイラ飼育記 メモ編の続き。地獄のHerculean taskを回避できそう。

Poly(C)の構成の要点は：

  1. Cに部分対称構造（partially symmetric structure/system）を導入する。
  2. Poly(C)とCの中間にPolyFull(C)を入れる。
  3. 多射の結合のために、フィラー（またはパディング）とグルー射の概念を導入する。

以下で、'LEFT RIGHT ARROW' (U+2194) を使う。→ http://www.fileformat.info/info/unicode/char/2194/index.htm

部分対称構造：

  • S⊆|C|×|C|
  • (A, B)∈S ⇔ A↔B という記号を使う。
  • A↔B かつ A\stackrel{\sim}{=}A' かつ B\stackrel{\sim}{=}B' ⇒ A'↔B'
  • A↔B ⇒ B↔A
  • A↔B かつ A↔C ⇒ A↔(B\otimesC)
  • A↔C かつ B↔C ⇒ (A\otimesB)↔C

以上が準備。S⊆|C|×|C| で添字付けられたCの射の族 σA,B (A, B)∈S を考える。σA,B:A\otimesB→B\otimesA。これがまず、バンドリング／アンバンドリング法則を満たす。

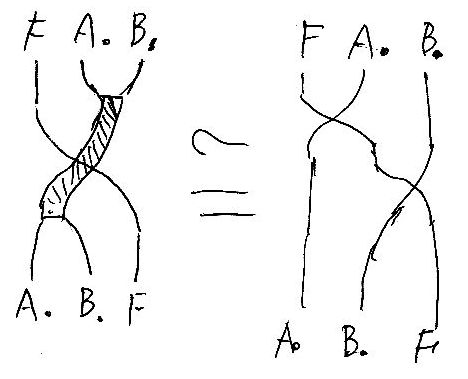
それと、ライデマイスターIIとライデマイスターIII（ヤン／バクスター）を満たす。それと、σA,B（クロス、クロッシング、スワップ）に沿ったクロススライディングが可能だとする。クロススライディングがあれば、ヤン／バクスターは出るけどね。次の検索を参照。

部分対称構造では、S = |C|×|C| を要求しない。このため、次の命題が成立する。

  • 任意のモノイド圏に対して、S = ({I}×|C|)∪(|C|×{I}) である部分対称構造が存在する。

↑命題の記述が雑で、実際には同型なものを全部取り込んでSを定義する。{I}の代わりに、Iと同型な対象全体を使う。

次は、PolyFull(C)。これは多圏ではなくて単なる圏。だけど、対象としては多対象＝Cの対象のリストを考える。多対象の連接をモノイド積として厳密モノイド圏になる。厳密になるところがミソで、これで扱いやすくなる。

Cの部分対称構造をPolyFull(C)にも持ち込める。つまり、PolyFull(C)は、部分対称厳密モノイド圏。

PolyFull(C)内に、Cの対称射（＝スワップ射）を取り込む。つうか、定義から自動的に取り込まれる。多圏の結合の定義は、PolyFull(C) を使って行う。

Poly(C)は、PolyFull(C)とほとんど同じ。違う点は、

  1. 結合可能性の定義が違う。
  2. 当然に、結合の定義も違う。

結合可能性は、f:Γ⇒Δ, g:Φ→Ψ に対して、

  1. Δ = Δ1, B, Δ2 という分解がある。
  2. Φ = Φ1, B, Φ2 という分解がある。
  3. Δ1↔Φ1 かつ Δ2↔Φ2

σ[Φ1, Δ1]\otimesidB\otimesσ[Δ2, Φ2] をグルー射と呼ぶ。

fとgにフィラー（パディング）を付けて、グルー射を挟んでPolyFull(C)内で結合したものが、多圏における結合結果。結合律と単位律は、定義から自動的に従う。やたっ。

非対称な閉圏（コンパクト閉圏だが）の例は、テンパリー／リーブ圏。関係圏と同様に自己双対コンパクト閉圏で、テンソル積（連言）と指数（含意）が一致する。論理は超コンパクト論理。

テンパリー（テンパリー／リーブ）の検索：

あと、

極性（荷電、符号）を付けたテンパリー／リーブ圏なら自己双対ではない。

2007年の閉圏、弱いラムダ計算、弱い論理 - 檜山正幸のキマイラ飼育記で言ったこと「任意の非対称モノイド閉圏でラムダ計算とシーケント計算をする」がやっと実現しそう。