絵の描き方とテンソル計算
絵の描き方と対応するテンソル計算について、ザット述べる。まずはこの図。
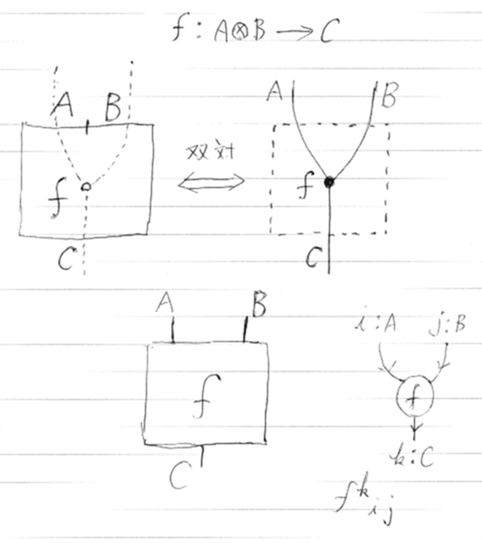
モノイド圏におけるf:A×B→Cの絵だが、左上はスタック図(サンチャゴ・ダイアグラム)。射が領域で、対象は領域の境界の一部、テンソル積は境界片の直和。この図とポアンカレ双対なのがストリング図。射が点、対象は辺となる。
boxes-and-wires図は中途半端な折衷で、射が箱、対象が辺。テンソル記法は、これらの図(どれでもいいが、ストリング図がいいだろう)をもとに、各対象(型ではなくてインスタンス)を区別できるインデックスを付けて、対象を上下添字で表現。暗黙にインデックスと対象(型)の対応が必要。
いまの図は、上から下の方向だったが、下から上の方向にした図。
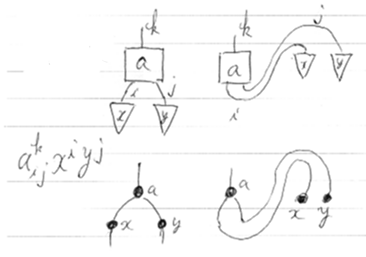
記法akijxiyjの解釈はイッパイアルのだが、そのうちの2つを描いておいた。(x×y);a と (η×I×I);(a×(B×A)×(x×y));(C×ε)。この2つの図を簡略化して点と線だけにしたものも描いた。これは、自然演繹証明図やラムダ計算でも出てくる図だ。
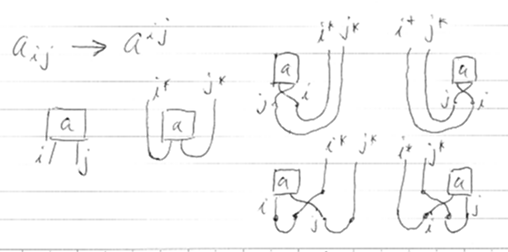
これ(↑)は、aijの添字を2つとも上げる例。絵では、双対対象に対するインデックスに星を付けているが、線に向きをつければ星は不要だろう。添字を上げた結果もいろいろな組み合わせがある。それらが同値であることは、コンパクト閉圏やダガーコンパクト閉圏で証明できるが、けっこう面倒。
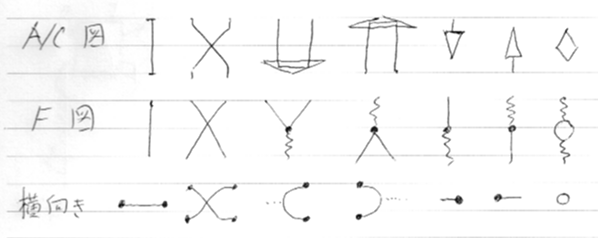
代表的な(って、他にもイッパイあるが)図式法をまとめておく。A/Cはアブラムスキー/クック、Fはファインマン。どちらも方向は下から上。