ヤンキング公式とフリップターン公式
以前、コンパクト閉圏における σA*,A;εA = εA* のような等式をツイスト公式(twisting formula)と呼んでいたが、ツイスト(ひねり、ねじれ、よじれ)は、別な意味で使うのでどうもマズイ。とりあえず、フリップターン公式(flip turn formula)にしておく。
ジグザグ公式、フリップターン公式(旧・ツイスト公式)、ヤンキング公式は互いに独立ではない。ヤンキングとフリップターンからジグザグを出す、という方針を採用したこともあったが、ジグザグは非対称モノイド圏でも意味があるので、ジグザグをより基本的だと考えるのがスジだろう。
ジグザグを仮定すると、組紐モノイド圏(braided monoidal category)でも、フリップターンとヤンキングが同値であることを示せる。次の形で理解するのがいいと思う。
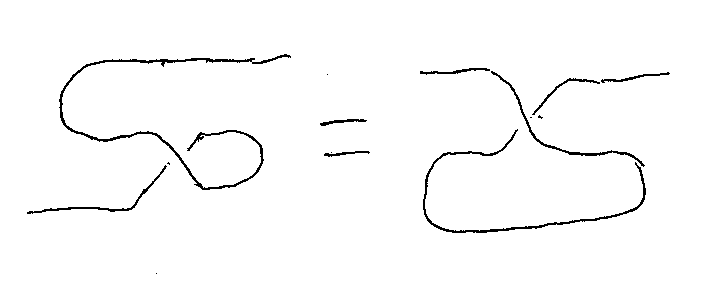
これは次のようにして示せる。1番の点線内を、クロスオーバー公式で変形。2番の点線内はライデマイスターIIに対応するブレイド群の計算。
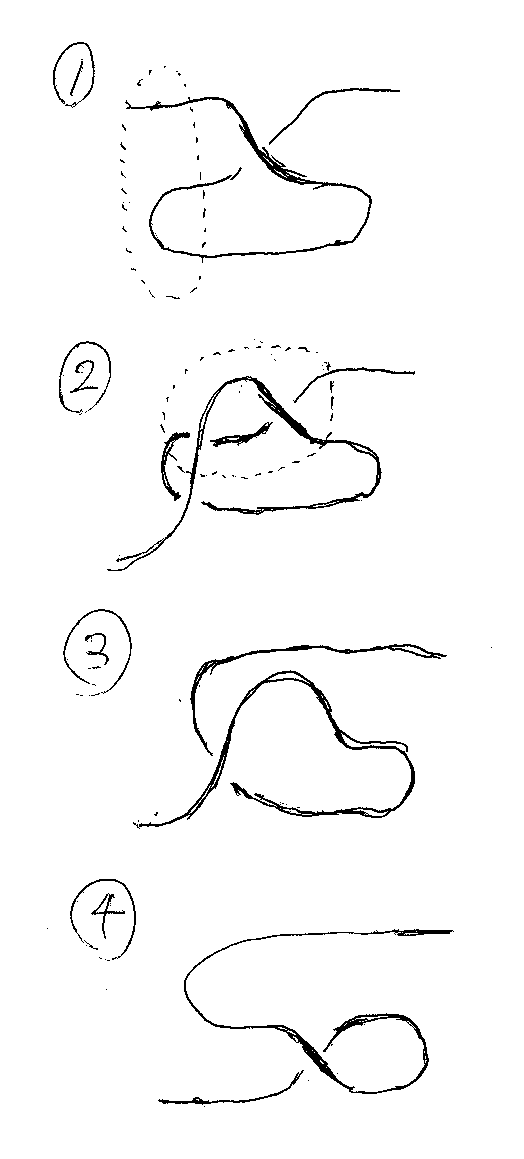
今示した同値性を使うと、「フリップターン→ヤンキング」は明か。「ヤンキング→フリップターン」は、下の図の点線内をヤンキングで直線に置き換えればよい。
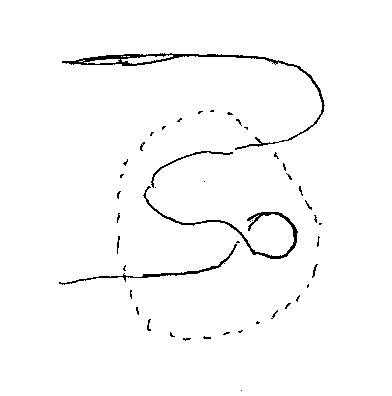
dualizer on objectsを持つモノイド圏でジグザグ公式が成り立つと、対称性がなくてもそれなりのことができる(軸的圏;pivotal category)。ジグザグに加えるべき性質にはフリップターンがいいような気がするこの頃。