ブレイド

論理やコンピューティングサイエンスの関係だと、対称モノイド圏はよく出てくるが、ブレイドモノイド圏（braided monoidal category）はあまり出てこないようだ。が、ちょっと調べておく。

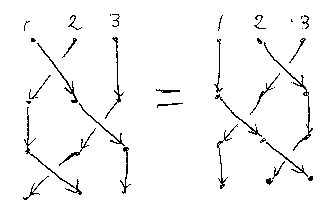
まず、アルチン（Artin）によるブレイド群（braid group）の定式化。ストランド（紐、毛髪）の数をnとして、ストランドを1, 2, ..., nで番号付ける。iとi+1を入れ替える交差（他はストレートにつなぐ）をβiとして、次がアルチンのブレイド関係式（braid relations）：

1. j ≧ i + 2 ならば、βi・βj = βj・βi （隣じゃなければ無関係）
2. βi・βi+1・βi = βi+1・βi・βi+1 （お隣の交差のあいだの関係）

βiは次の図のようだが、βiとその逆βi^-1は入れ替えても何も変わらないので、どちらをβiと思ってもよい。

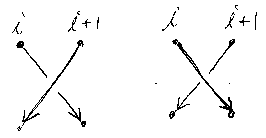
左から右へのストランドが上に来る交差を基本として（それが僕の好み）考えると、アルチンのブレイド関係式は次の図になる。

図の描き方を少し変えてみると、ライデマイスター移動（Reidemeister moves）のひとつになる。

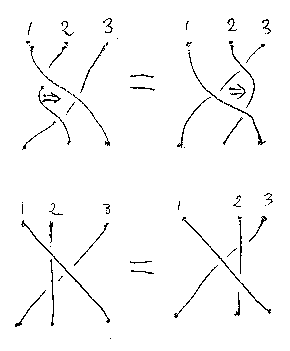
圏論的に定式化するため、σ_A,B:A+B → B+A を導入する。σの逆をσ'と書く。逆なのだから：

• σ_A,B;σ'_B,A = A+B
• σ'_B,A;σ_A,B; = B+A

ブレイド関係式は：

• (σ_A,B + C);(A + σ_B,C);(σ_A,B + C) = (A + σ_B,C);(σ_A,B + C);(A + σ_B,C)

ところで、ライデマイスター移動は3種あるのだが、1つ目はσとσ'が互いに逆であること、2つ目はアルチンのブレイド関係式になる。そして3つ目は、トレースのヤンキングになっている。ただし、Tr(σ_A,A) = A^* になっているようだ。トレースとはいっても、双対（逆向き）が必要なので、最初からコンパクト閉圏を考えることになる。コンパクト閉なブレイド圏は、物理がらみで別な呼び方があるようだ。

ブレイド圏だと、σを何度も続けると、お下げ髪のような編み込み紐ができる。これをほどくにはσ'をcomposeする必要がある。直感的はこれが自然で、対称ブレイディングは不自然な感じがする。まー、計算は簡単だからいいのだけど。