スパイダーグラフ (2)
スパイダーグラフ (1) の続き。
スパイダー射の意味論
スパイダー射は、f: A → B1, B2, ... Bn という、余域側に複数の型を並べていいプロファイルを持つ。複数の出力チャンネルを持つわけだ。複数の出力の一番お馴染みの例は、標準出力(stdout)と例外(exception)である。Catyの記法で、f :: A -> B throws E ならば、f:A → B, E というスパイダー射となる。f :: A -> B throws [E, E'] ならば、f:A → B, E, E' である。
標準出力と例外は違った出力チャネルだが、スパイダー射ではそれを特に区別しない。Catyでは、例外と類似のシグナルという機構がある。例外とシグナルは通常同じメカニズムで実装されるが、シグナルはエラーではなくて正常な大域脱出となる。f :: A -> B throws [E, E'] signals S は、f:A → B, E, E', S というスパイダー射となる。
CatyScript 2.0では、標準入出力のパイプライン結合以外に、forward制御やbegin/repeat制御が導入されている。これらのgoto-like制御によるフローも、スパイダー射では通常の出力と同様に扱う。
つまり、言語仕様や実装のレベルでは異なる扱いとなる出力チャネルを同等に扱ったフローグラフがスパイダーグラフである。スパイダーグラフの「ノード(蜘蛛の胴体)とノード近傍(蜘蛛の脚)」をスパイダーノード(蜘蛛の胴体と脚=スパイダー射の図式表現)と呼んでいる。
ソフトウェア的には正常処理とエラーは違うと思われているが、その違いは微妙なことも多い。ときに恣意的でさえある。また、標準入力かパラメータかの区別も偶発的/恣意的と言える。これらの恣意性は忘れて、単に複数の入出力チャンネルがあると捉えたのがスパイダーグラフだ。
CatyScriptの直列実行エンジンは、時系列に沿ってスパイダーグラフ上の1本の経路をたどる。並列実行エンジンなら、同時に複数の経路をたどることになる。スパイダーグラフの計算ノードに制御が移り、そこで計算が実行されることを、そのノードが発火すると言うことがある。直列実行エンジンでは、同時に発火する点は高々1個。並列実行エンジンでは、同時に複数の箇所が発火可能である。
発火点の時間的な変動では、直列実行エンジンでは粒子の運動の軌道、並列実行エンジンでは波の進行のように記述される。スパイダーグラフは並列実行を仮定しているので、それを直列実行エンジンで実行するときにはバックトラック経路を付け加える必要がある。バックトラック経路を付け加えれば、スパイダーグラフを一筆書きできる。その一筆書きの跡が直列(逐次、順次)実行の運動軌道となる。
火が燃え移る、燃え広がる感じをほんのちょっと味わえるページ↓
エリア
エリアとは、グラフを描く平面内の境界線で区切られた領域である。手描きのときは、任意の不定形の領域を使ってよい。プログラム書きだと、矩形や楕円に限定されるだろう。
グラフを描く全体領域もまたエリアと考えて、これをルートエリアと呼ぶ。概念上は空エリアを考えることができるが、実質的には無意味であるので、描画では考えない(無視する)。
データ構造としてのエリアは、ノードの集合である。グラフのノード全体の集合をNとして、「Aがエリアである」とは「A⊆N」という意味になる。ノードの集合(グループ)を視覚的に識別するために、境界付きの領域内にまとめて配置する。
Aがエリアで、eがグラフの辺(edge)のとき; source(e), target(e)∈A ならば、eはエリアの内部辺(domestic edge)と呼ぶ。 描画のときも辺は領域から出ることはない(レイアウトによっては、チョットはみ出すかも)。複数のエリアをまたがる(エリア境界を超える)辺はインターエリア辺(inter-area edge)と呼ぶ。
エリアの入れ子構造
お約束: A⊂B は、「A⊆B であり、A≠B」を意味する。つまり、A⊂B は、AがBの真部分集合であることを意味する。
ノード全体の集合をNとして、Nの部分集合の族をSとする。A∈S と A⊆N は同じ意味。Sが適性にネストしている(properly nested)とは次のこと:
Sが適正にネストしているなら、Sの要素をノードとしたツリー構造を持つ。「Sの要素=Nの部分集合=エリア」なので、ツリー構造はエリアのツリー構造となる。
グラフに指定されたエリアの集合が適正にネストしているときは、エリアを平面領域にする以外に、エリアをノードとしたツリーも描ける。元のノードを末端ノード(リーフ)、エリアを中間ノード(分岐ノード)、もとのノード全体を表すNをルートとするツリーを描くこともある。
多くの応用では、エリアの集合は適正にネストしている。具体例は、モジュールをノード、エリアをパッケージとするグラフ構造である。
エリアの事例
エリアを持つようなグラフの例には次がある。
| ノード | エリア | 全体 | 該当する図 |
|---|---|---|---|
| フラグメント | アクション | アクション近傍 | アクションの図 |
| アクション | リソース | モジュール | モジュールの図 |
| コマンド | ブロック/フラグメント | スクリプトコード | スクリプトコードの図 |
| モジュール | パッケージ | アプリケーション | アプリケーションの図 |
| コントロール | サブシステム | システム | ロバストネス図 |
ポート
ポートとは、仮のノード/ノードの代理のようなものだ。ポートはエリアとの関係で論じられる。とりあず描画法だが、次のように描くことにする。アウトバウンドポート(またはアウトレット)は、エリアから出ていく出口。インバウンドポート(またはインレット)は、外部からエリアに入る入口。
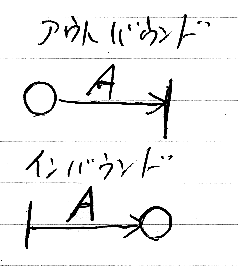
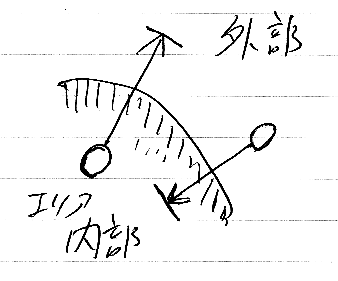
ポートはエリアに所属する。アウトバウンドポートは、根元をエリア内に、矢先をエリアの外に出す。結果としてポートの線はエリア境界を横切ることになる。インバウンドポートは逆向きに配置する。(次の図、インバウンドポートが形状がちと間違っている、まーいいや。適当に修復してちょ。)
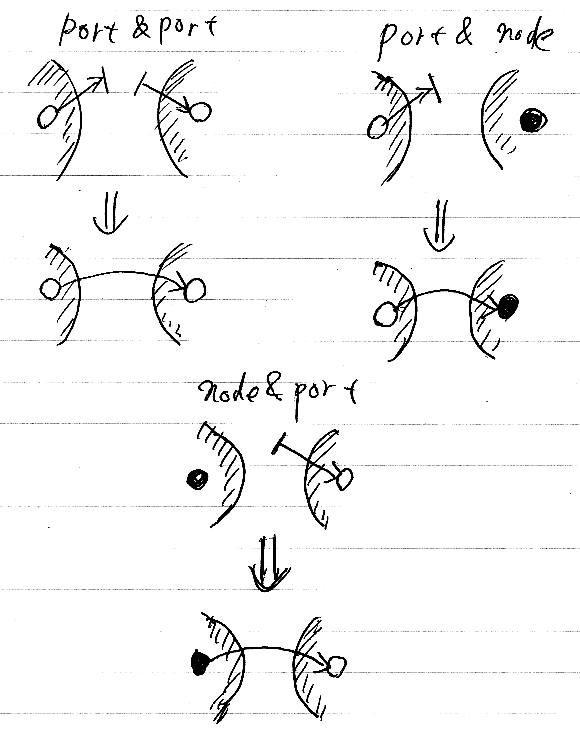
ポートの結合(束縛)
ポートは結合される。ポートどうしの結合、ポートとノードの結合が2種で、合計三種類の結合がある。下向きの「⇒」は結合操作を表す。
リレー
いくつかの辺とノードを経由して2つのノードのあいだを結ぶことができる可能性(可達性)を示す辺をリレー辺と呼ぶ。リレー辺は、現状は茶色の点線になっている。まー、適当な描画法で示せばいい。