ベックの法則にまたまた遭遇！

可換モノイドによるモノイダルスタンピングモナドから作ったクライスリ圏に対称モノイド積を入れようと試みて、次の等式（つうか同型）が必要になった。

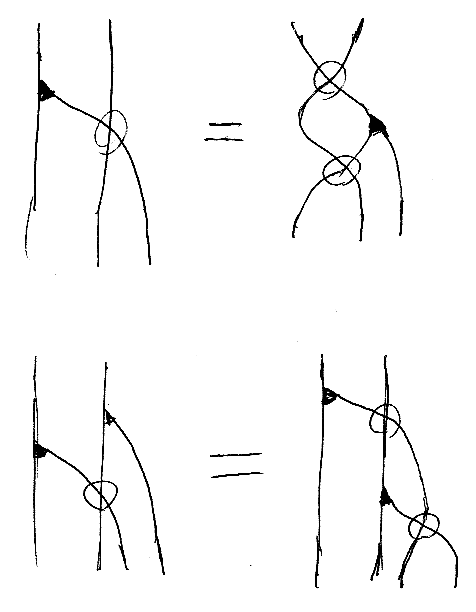
少し書き換えてみると：

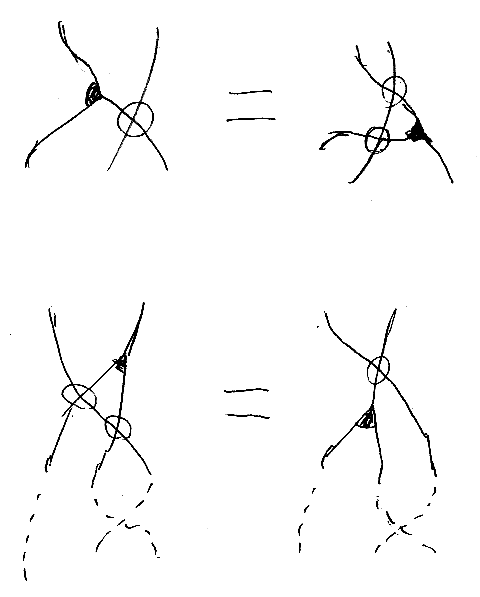
さらに一部と取り出して、整理したら次のようになる。

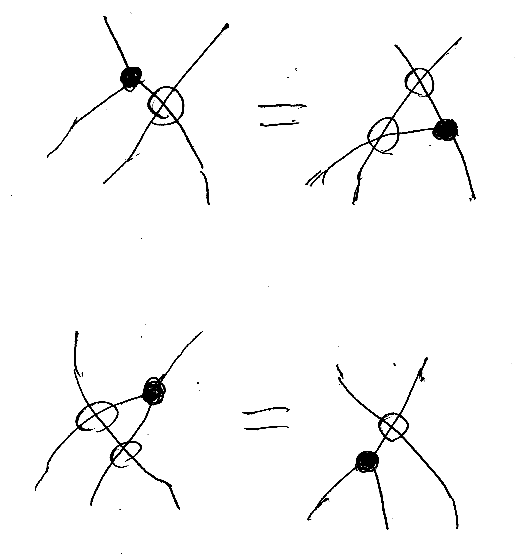
これってベックの分配法則だろう！ また出てきたよ。

有向グラフの書き換えだと思うと、「3価（trivalent）のノード1個と4価のノード1個」が「3価のノード1個と4価のノード2個」に変形する。3価ノードは、二項演算または余二項演算（余二項余演算）を表す。4価ノードはベックのスワッパーだ。3価ノードが二項演算または余二項演算を表す状況は物理とかでもやたらに出てくる。フュージョンとか呼ばれているのがそうだと思う（詳しくは知らんが）。

一般的には、(n + 1)価のノードが演算／余演算、4価のノードがスワッパーだとして、結合性、交換性（ブレイドもあり）、分配性（ベックの法則）の議論が絵算的にできるのだと思う。スワッパーの定式化には、バンドル・アンバンドル（バンドリング・アンバンドリング）構造を使うのがよさそう。