田辺さんの単純平面タングル（SPT）圏デモの画面ショット

本編 http://d.hatena.ne.jp/m-hiyama/20090623/1245715012 とまったく同じエントリーですが、画面が原寸大です。

「田辺さんの圏論デモ、こりゃオモロー」で紹介した田辺さんのエントリーに、画面も付きました。

• http://monado.dtiblog.com/blog-entry-74.html

田辺さん、ありがとうございます。

それとは別に、某太田君が画面ショットを送ってくれました。どうもありがとね。メール文面を引用：

太田です。
静止画ですが、各パターン撮ってみました

4つの円を左から　1、2、3、4としています。
あの後遊んでいたら、1，2とか3，4という組み合わせだと

延々繋がることがわかりました。
 - 1，2の組み合わせだと必ず交互

 - 3、4の組み合わせだと3、3とかも可

↓が初期状態の画面。

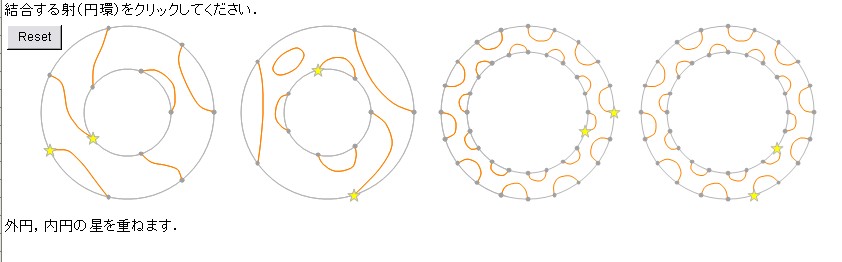
「4つの円を左から　1、2、3、4としています。」ということです。

それで、↓は1番と2番の結合。下側に結合の結果が描いてあります。静止画だと分かりにくいけど、1番が2番の穴にはめ込まれてグリグリと回転して位置合わせして、それから境界（円環内部の円）が消えるんだよね。

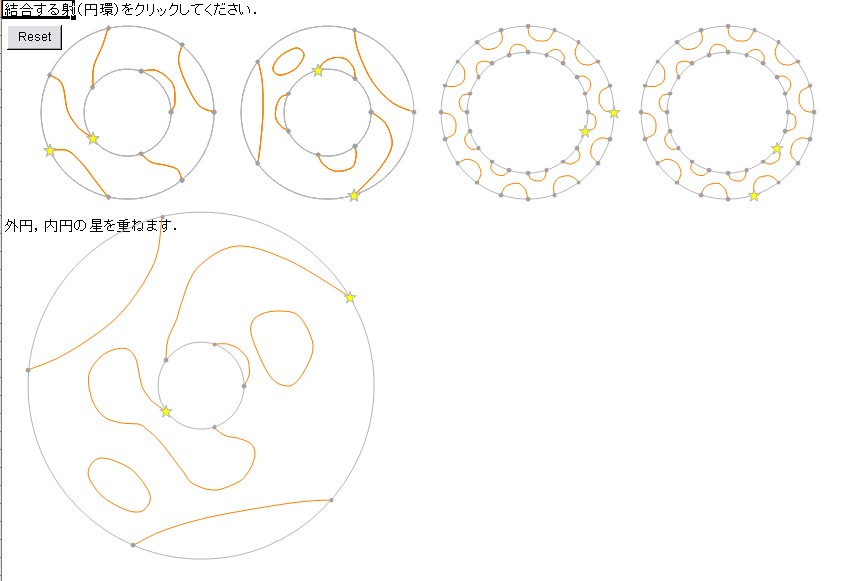
↓は3番と4番の結合。

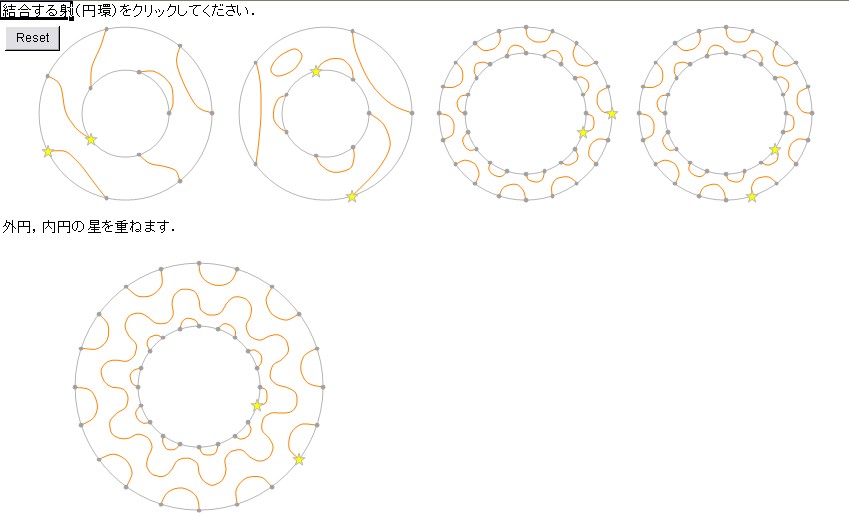
次は2番、1番の順で結合↓ 1番、2番のときと比べてください。

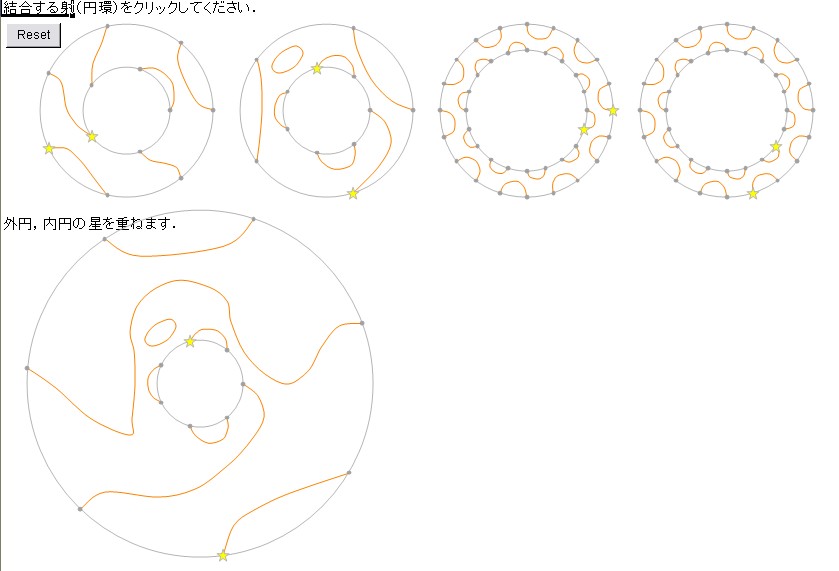
↓は4番と3番。3番と4番とは違うでしょ。

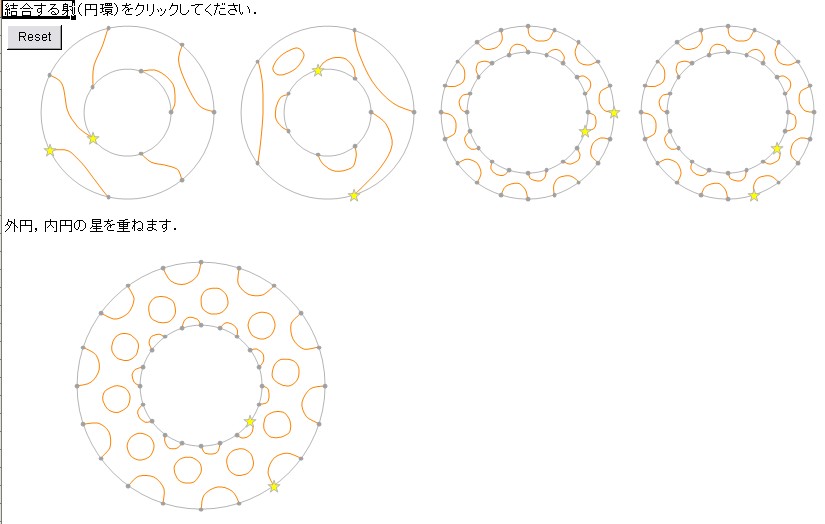
3番と3番も結合可能でこんな↓ 1つ前と同じじゃないよ、星の位置に注意

---

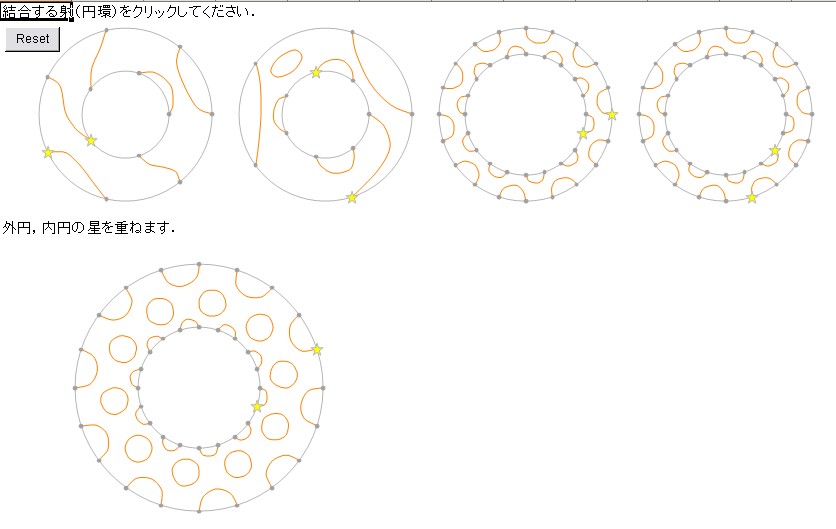
太田君の“発見”についてチョット言っておくと； 4つの射（ヒモ模様）を左から A1, A2, A3, A4 として、円周上の点の個数を勘定すれば、射の域／余域はわかります。次のとおりです。

1. A1:5→7
2. A2:7→5
3. A3:20→20
4. A3:20→20

射の結合可能性（composability）から、A1;A2、A2;A3 などは作れますが、A1;A3 とかは無理です。

太田君曰く：

• 1，2とか3，4という組み合わせだと延々繋がることがわかりました。

A1;A2;A1;A2 とか A3;A4;A4;A3;A3 とかも作れるってことです。

• 1，2の組み合わせだと必ず交互
• 3、4の組み合わせだと3、3とかも可

これは、それぞれの射の域／余域と結合可能性からの帰結です。