「ラムダ計算、論理、圏」の予習・復習のために
※日付はダミー:実際の執筆・公開日は2009-03-14
最初にホワイトボードの写真があって、その直後に説明があります。(本編の「紙芝居:ラムダ抽象」とは、写真/説明の順序が逆ですね ^^;)
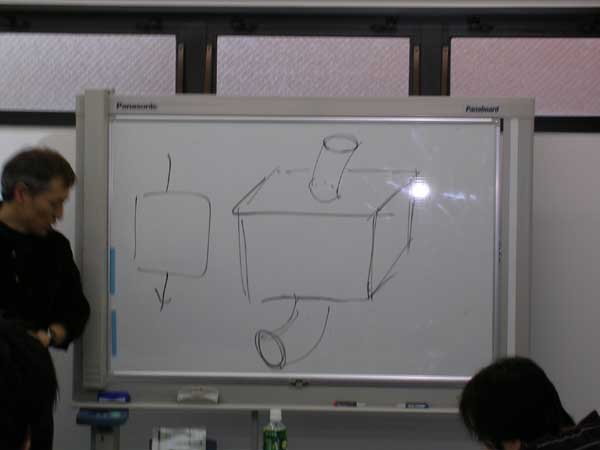
関数は昔「函数」と書いてたのよ。「函」は函館のハコだから「箱」の意味。で、箱の絵を描くわけだが、毎回リアルな箱やパイプを描くのは大変だから、四角(ボックス)と線(ワイヤー)で描くよ。
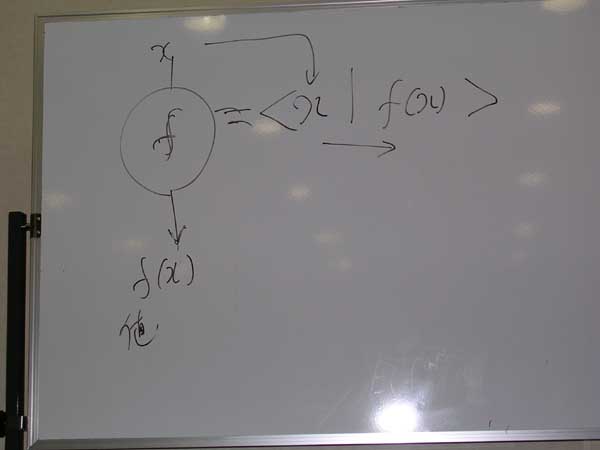
四角も面倒ならオダンゴ(丸)でもいい。このセミナー内では、関数の向きは上から下だとする。関数をテキストで表現するときは、<x | f(x) > のような書き方をする。入力変数(引数変数)がxで、f(x)のところには、fを表現する式を書いてもいい。
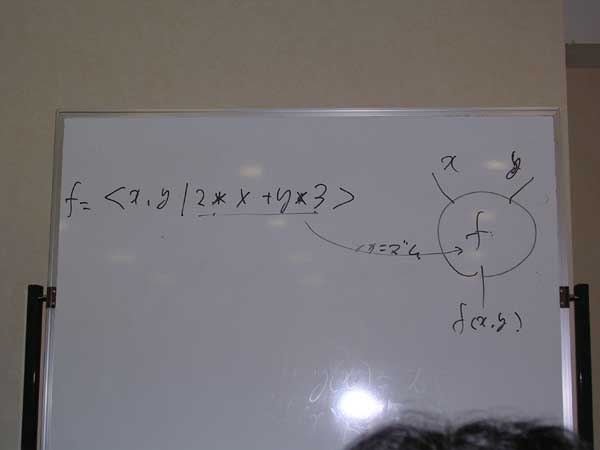
例えばこれは二変数(二引数)の関数。fは、2つの変数xとyからf(x, y)を算出するメカニズムを持つから、そのメカニズムを 式 2*x + y*3 とかで表す。
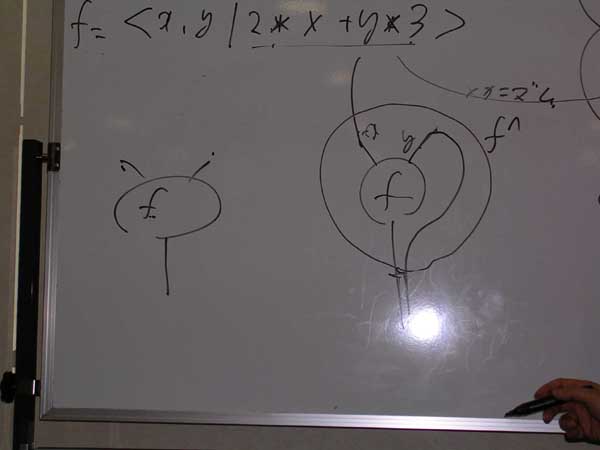
さて、関数のカリー化=ラムダ抽象だが、図では右の入力ワイヤーを曲げることになる。カリー化をしたfをf^と書く。2回カリー化したらf^^だね。
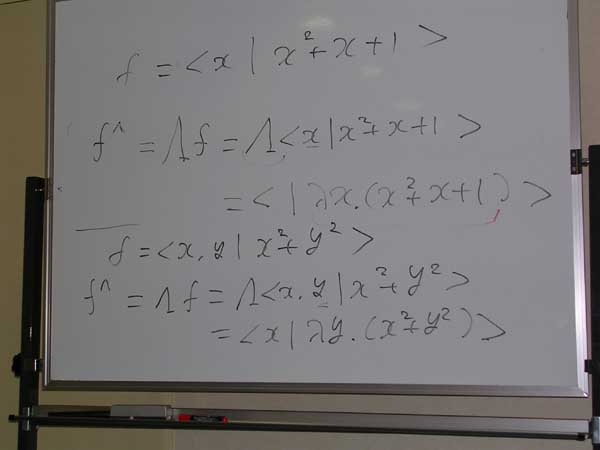
fが一変数関数 f(x) = x2 + x + 1 のとき、f^の計算はこうなる。大きなラムダ括弧('<'と'>')の内部にある式に、小さなラムダ'λ'がかかることになる。
fが二変数関数 f(x, y) = x2 + y2 のときは、ホワイトボードの下半分のようになる。右側の変数yだけがλで束縛される。xはそのままだよ。
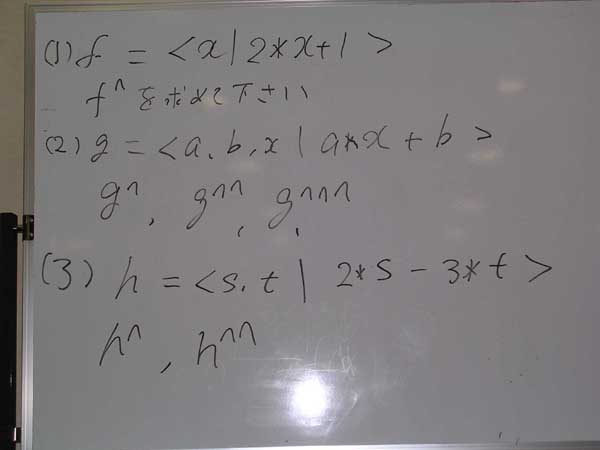
ここらで練習問題だ。
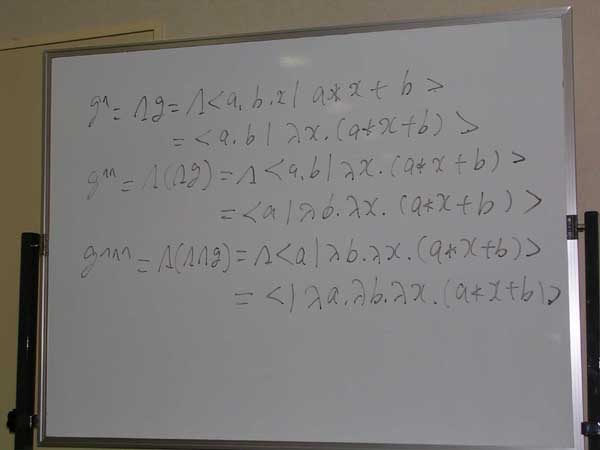
g(a, b, x) = a*x + b だけやってみよう。g^, g^^, g^^^ はこんな感じに計算できる。
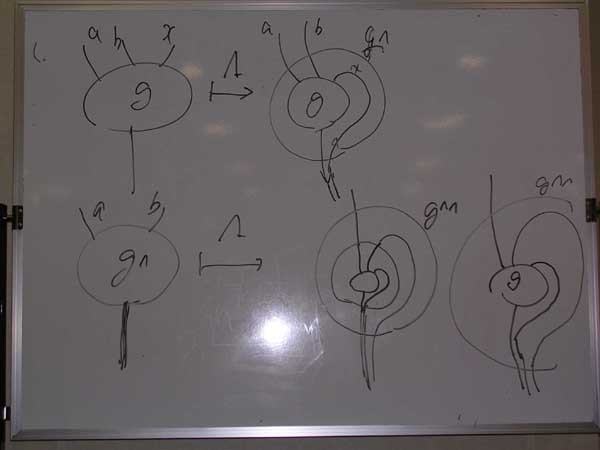
gからg^、g^からg^^を作る操作(それがカリー化=ラムダ抽象)を絵に描くとこんな。
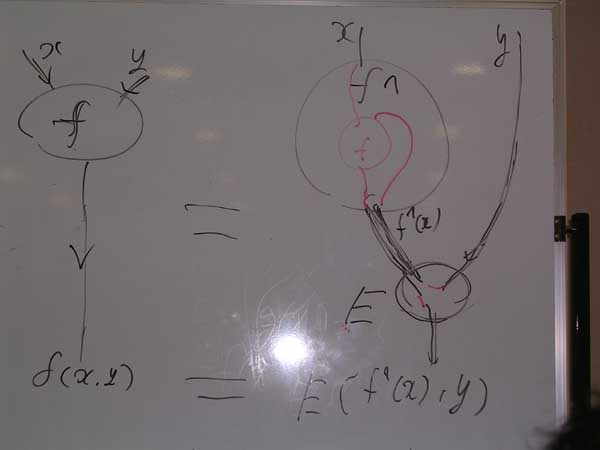
ラムダ計算で一番大事な法則がこの等式だ。
fからカリー化されたf^を、実行エンジン(evaluator)Eに渡してあげれば、もとの関数fを再現できる。f^は、fの右ワイヤーを曲げたものだったけど、その状況は赤で描いてある。

この図は、f(x, y) = x + y のケースで、f^とf^^を描いたもの。実行エンジンは、曲がったワイヤーが集まる場所として描いている。バエズは、ワイヤーが集まる場所=実行エンジンの部分を“evalバブル”と呼んでいる。そのココロはベータ変換によりハジケテ消えてしまうから。f^を囲む外側のマルもバブル(ラムダバブル)で、やっぱりベータ変換によりハジケテ消える。
下の絵は、f^ と E の簡略記法。f^なら二重丸、f^^なら三重マル。ワイヤーも本数分だけ束ねた絵にする。描くのが少し楽になるよ。