有向グラフの指数（exponentiation）をもっと調べる

「有向グラフの指数（exponentiation）」の続き。A^Aが3頂点6辺だという別な状況証拠を示します。当該のAは、2頂点3辺（うち非自明な辺は1本）の反射的有向グラフ（を指す固有名詞）でした。Aはまた、二元集合を台集合（underlying set）とする線形順序構造ともみなせました。

辺集合と頂点集合はホムセットで表現できる

反射的有向グラフの圏をRDGとして、任意のグラフBに対してホムセットRDG(A, B)を考えましょう。f∈RDG(A, B)は、f(s), f(a), f(t)で決まるBの辺を特定します。逆に、Bの辺e:x→yがあれば、f(s) = x, f(a) = e, f(t) = y として射f:A→Bが決まるので、RDG(A, B) ＝ Edge(B) 。

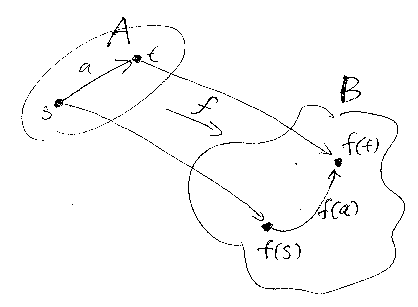
A^AがRDG内に存在すると仮定して、特にBをA^Aにすれば：

• RDG(A, A^A) ＝ Edge(A^A) ……(edge)

Aの代わりに、1頂点1辺の自明なグラフをIとすると、RDG(I, B) ＝ Node(B) が得られます。BをA^Aにすれば：

• RDG(I, A^A) ＝ Node(A^A) ……(node)

等式（つうより同型式）(edge)と(node)から、A^Aの辺集合と頂点集合は、特別なホムセットRDG(A, A^A)とRDG(I, A^A)で与えられることがわかりました。で、RDG(A, A^A)とRDG(I, A^A)を探ることにします。

補題としてクイズを解いておこう

直積グラフA×Aを作ると、下図の左のようになりますが、それは、順序集合としては“いわゆるダイヤモンド束”と同型です。

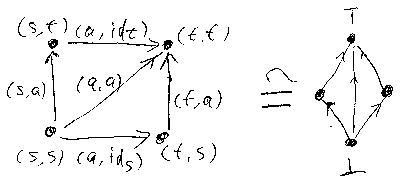
上記の四元ダイヤモンド束をDとして、次のクイズ問題を考えます； Dを、D = D₀ + D₁ と直和に分解する。このとき、x∈D₁, y∈D₀、x ＜ y となるようなx, yが生じないような分解は何通りあるか？ つまり、D₁のメンバーがD₀のメンバーの下に来るのを許さないようなD₀, D₁への分割法を列挙してください。

答えはコチラ。

そういう分割は単調写像と同じこと

さてと、Aの二元を一時的に便宜上{0, 1}（sを0, tを1）として、四元ダイヤモンド束Dから二元線形順序集合Aへの単調写像fを考えます。逆像f^-1(0)、f^-1(1)をそれぞれD₀、D₁とすると、上のクイズ問題の条件を満たします。正確に言うと：

• 単調写像f:D→A と、上のクイズ問題の条件を満たす分割 D = D₀ + D₁ は一対一に対応する。

このことは、∀x, y∈D.[x ≦ y ⇒ f(x) ≦ f(y)] をゴニョゴニョして、¬(∃x, y∈D.[x ＜ y ∧ f(x) = 1 ∧ f(y) = 0]) まで変形、とその逆ができればいいですね。

もし、積とベキの随伴が使えれば、辺集合がわかる

ここで、圏RDG上の自己関手について考察。“Aを直積で掛け算する関手(-)×A”と、“Aをベキ指数に載せる関手(-)^A”が、もし随伴ならば、任意のグラフG, Hに対して次の同型があるはずです。

• RDG(G×A, H) ＝ RDG(G, H^A)

特に、G = H = A と置けば：

• RDG(A×A, A) ＝ RDG(A, A^A)

A×A ＝ D （Dはダイヤモンド束）だったので、RDG(A×A, A) ＝ RDG(D, A)。RDGにおける射f:D→Aは、順序構造の単調写像とみなしてよいので：

• RDG(A×A, A) ＝ RDG(D, A) ＝ Monoto(D, A) ＝ {D₁がD₀の下に来ないようなDの分割}

この等式（同型式）の最後の集合はクイズの答えから6元でした。

右辺であるRDG(A, A^A)は、(edge)から Edge(A^A)だったので、随伴の同型RDG(A×A, A) ＝ RDG(A, A^A) は：

• Monoto(D, A) ＝ Edge(A^A)

と解釈できます。そんなわけで、Edge(A^A)が6元であるとわかりました。

頂点集合もわかる

もう一度、随伴の同型に戻って：

• RDG(G×A, H) ＝ RDG(G, H^A)

G = I、H = A と置けば：

• RDG(I×A, A) ＝ RDG(I, A^A)

右辺は冒頭の(node)から、Node(A^A)ですが、左辺RDG(I×A, A)はRDG(A, A) ＝ Monoto(A, A)、よって：

• Monoto(A, A) ＝ Node(A^A)

まとめると

A^Aの辺集合、頂点集合は、それぞれ Monoto(D, A)とMonoto(A, A)で与えられます。これらは6元、3元。

ただし、圏RDGで、Aによる積とベキが存在して随伴であることを仮定しているので、ホントに随伴であることを確認する必要があります。積因子／べき指数をAに限れば、それほど難しくはないでしょう。