このブログは、旧・はてなダイアリー「檜山正幸のキマイラ飼育記 メモ編」（http://d.hatena.ne.jp/m-hiyama-memo/）のデータを移行・保存したものであり、今後（2019年1月以降）更新の予定はありません。

今後の更新は、新しいブログ http://m-hiyama-memo.hatenablog.com/ で行います。

モニャドセミナー4 資料 抜粋 ＋ 追加

M4 Mx

追加分は最後。

前置きとか予定とか（ほとんど）省略

  1. スタンピング・モナド（or コモナド）に限定
  2. 現実のプログラミングやシステムとの関係を強調する
  3. ラップ／アンラップが基本的な道具だよ
  4. 目標は、トランザクション計算（エコ計算）の、作用付き両クライスリ圏の構成

箴言集

  1. 対象に要素（元）があると思うな。あっても使うな。（「初等的」って言うのだ）
  2. 認識や分類は観察者の主観であって、対象物側にあるのではない。
  3. 態度を変えれば、同じ対象物に違う構造が見えてくる。違う構造は違うモノ。
  4. 極めてツマンナイものに注目する。空、単元集合、pointing map、自明モノイド（いくつかの意味がある）、包含写像、射影、忘却関手など。
  5. 用語・記法の歴史的な経緯や事情はあきらめろ。いまさらどうにもならない。（が、檜山はあきらめが悪い。）
  6. 記号はいつだって足りない、ホントに足りない。A, B, C∈|C| -- アリッ!?
  7. ズボラな記法や用法に慣れる。idA = A とかは、計算上も重要なズボラ・テク。

モノイドとコモノイド

  • 特に今日は、整数の足し算（カウンタ）、文字列の連接（テキストファイル）、2次元アフィン変換（タートル・グラフィックス）を考える。
  • [追記]タートルが2次元アフィン変換はほぼ嘘だった。砲台モナドを作るつもりだ。[/追記]
  • モノイドの矢印をひっくり返せば、コモノイドの定義と法則
  • 今日使うコモノイドは一種類、演算の名前は色々：対角、余積（余乗法）、余加法、複製、分岐などなど。

今日取り扱う圏と関手

Mはモノイド、Vはコモノイドと約束する。

記号 短い説明
C 基本とする圏、モノイド積を持つ
C×M Mによる右スタンピング構成（で得られた圏）
M×C Mによる左スタンピング構成
M×S M-加群Sによる右スタンピング構成、左も使うかも
RM Mによる右スタンピング（右掛け算）関手 C→C
LM Mによる左スタンピング（左掛け算）関手 C→C
Kl(RM) 右スタンピング・モナドRMのクライスリ圏
Kl(LM) 左スタンピング・モナドLMのクライスリ圏
CoKl(LV) コモノイドVによる左スタンピング・コモナドLVの余クライスリ圏
DiKl(LV, RM) 両（双）クライスリ圏
AcDiKl(LV, RM) 作用付き両クライスリ圏
  • モノイド積の典型例は直積
  • M-加群は線形代数の用語を拝借。M-作用を持つ対象。
  • RA, AL と書くと具合がいい。

その他、重要な関手

  • J : A×C→C -- スタンピング構成した圏から、もとの圏へ
  • W : Kl(RM)→C×M ラッピング
  • W' : Kl(RM)→C×S ラッピングもどき、一番わかりやすいが、アンラップ（中身の取り出し、再現）ができない
  • W : Kl(LV)→V×C ラッピング
  • W : DiKl(LV, RM)→V×C×M ラッピング
  • W : AcDiKl(LV, RM)→V×C×M ラッピング

スタンピング構成

今日ずっと基礎にする圏C -- 背景圏、環境（アンビアント〈アンビエント〉）圏。

  1. なんらかのデータ型、データ領域が対象
  2. なんらかの計算処理／計算主体が射
  3. 計算処理／計算主体を計算エージェントと呼ぶことがある
  4. 計算エージェントは内部と外部をわかつ境界を持っている
  5. 入出力は、n-in m-out または、タプリングを許して 1-in 1-out

A∈|C|を固定して、次の圏を作れる。

  • 対象は A×X の型のCの対象
  • 射は、A×X→A×Y の形のCの射
  • dom(f:A×X→A×Y) = X
  • cod(f:A×X→A×Y) = Y
  • compはfのcomp

この圏を A×C、面倒だから A×C と書く（これはイイカゲン過ぎてヤバイ）。[追記](A×)C くらいで手を打つか？[/追記]

ホムセットによる定義がいいかも。

関手J

J: A×C→C

  • J(X) = A×X
  • J(f:X→C in A×C) = (f in C)

このJは現実的にどんな意味があるか？

  • X→Y が、Cでは A×X→A×Y ってことは、、、
  • クラス定義を固定しての、、、
  • ×××を素朴な純関数計算で表してみると

数式と現象

  • 二次関数を学び、ちゃんと使える人はたくさんいる。
  • その二次関数で、「投げたボール」を記述できて、到達点を計算できることを知らない人はたくさんいる。
  • 小中学校の素材のなかにも、あれだけ圏が発見できる。
  • プログラミングやシステムの「現象」に、圏やモナドが含まれてないハズはないでしょ。どう考えても。
  • ヒープ（共有領域）もスタック（プライベート領域）も、参照引数も値引数も、イミュータビリティもディープコピーも、クラスとオブジェクトも、単一代入も、DIも、総称関数も依存型も、当然に圏論で現象記述（定式化）できるよ。当たり前だ。

今日のモノイドさん、モナドさん

  1. 有限カウンタ 0から9 有界 →カウンター・モナド - 檜山正幸のキマイラ飼育記 メモ編
  2. 有限カウンタ 0から9 サイクリック（ラップアラウンド） →サイクリック・カウンター・モナド - 檜山正幸のキマイラ飼育記 メモ編
  3. 出力モードのテキストファイル
  4. タートルグラフィックス ペンなし →タートル・モナド - 檜山正幸のキマイラ飼育記 メモ編
  5. タートルグラフィックス ペンあり
  • 状態値と作用値と遷移
  • あるいは、位置と力と運動

それっ、クライスリ圏

実例で考えると、状態空間への更新リクエストAPIを使う関数だよね。

ラッピングを使ってみよう

  • オブジェクト指向風の実行環境の上で実装するってことだね
  • アンラップできるところがミソ
  • アンラップがあるので、ラッピングは単射（埋め込み）
  • 既にクライスリ圏を作っているので、ラッピングは関手だと言っていい

ラッピングを先に考えると

Dがマグマ、Cが圏、F:D→C という対応があり：

  1. Fは単射
  2. Fはマグマの結合演算を保つ

このとき、Dは半圏であり、Fは半関手。

さらに、Dが反射的マグマ、Cが圏、F:D→C という対応があり：

  1. Fは単射
  2. Fはマグマの結合演算を保つ
  3. Fはマグマの恒等を保つ

このとき、Dは圏であり、Fは関手。

以上の事実を使って、クライスリ圏を構成してみよう。

余クライスリ圏

対角コモノイドのコモノイダル・スタンピング・モナドから、反射的マグマを作り、
余クライスリ圏も作ってしまえ。

状態スタンピングはイマイチ

ラッピングに近いことができるが、作用がどうなっているか外部からは予測できないので、アンラップできない。アンラップがないので単射性が示せず、埋め込み関手が構成できない。

もう少し工夫しないと。

ここらで愚痴を言っておきたい

「… だーから右と左のハナシはいやなんだよなー」

  • (a・b)*x = a*(b*x) 気持ちいい左作用
  • (a・b)*x = b*(a*x) 気持ち悪い左作用
  • x*(a・b) = (x*a)*b 気持ちいい右作用
  • x*(a・b) = (x*b)*a 気持ち悪い右作用

前回（モニャドセミナー3）でも間違えたしよ。

「理解をさまたげるモノ／誤解をまねくモノ、それと対処」のの「右と左、上と下、前と後」参照

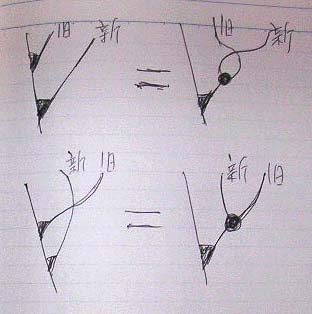
加群（作用）の公理

カウンタ、テキストファイル、タートルグラフィックスが例。

結合律を絵で表そう。

後はなりゆき

クライスリ圏の一般論はたぶんやらないと思うが、 やらない。

後はなりゆき 2

次の計算はアドリブでは不安だ。写真を載せておこう。

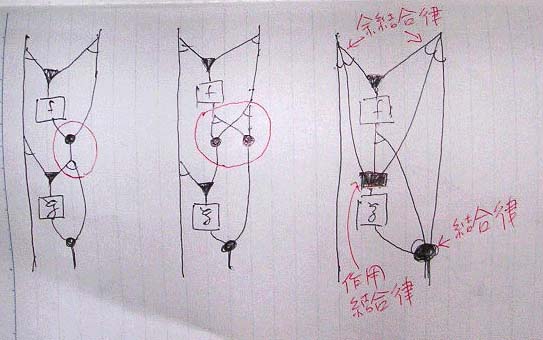
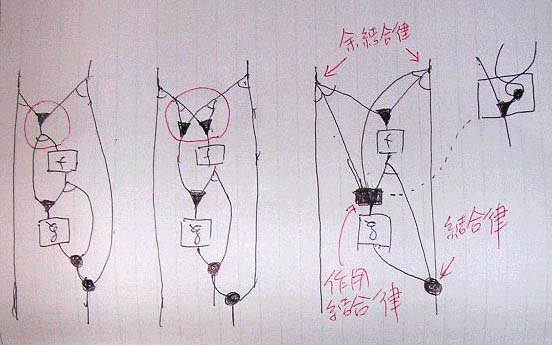
あと、双モノイド法則（3種4種）が必要だが、それはアドリブ。

ここから追加分

ちょっと練習問題

  1. 値が{0, 1}だけの有界カウンタの標準的（常識的に自然な）オペレーション・モノイドを記述せよ。
  2. モノイド{u, d}* （星はクリーニスター）から、すぐ上のオペレーション・モノイドへのモノイド射（準同型）を記述せよ。
  3. 値が{0, 1}だけのサイクリック・カウンタの標準的オペレーション・モノイドを記述せよ。
  4. モノイド{u, d}* から、すぐ上のオペレーション・モノイドへのモノイド射（準同型）を記述せよ。
  5. モノイド{u, d}* ではなくて、Z（整数）の足し算モノイドからのモノイド射を記述せよ。
  6. モノイド{on, off, toggle}* から、End({0, 1})への常識的なモノイド準同型を記述せよ。
  7. モノイド{on, off, toggle}* に関係を入れて、End({0, 1}) と同型なモノイドを作れ。
  8. 平面格子内を動く、マウス・グラフィックスの状態空間とモノイドを定義せよ。

状態空間スタンピングがダメな理由

  1. モノイド作用が計算エージェント内に分離不可能に組み込まれている
  2. アンラップできない
  3. 作用の取り替えができない
  4. よって、柔軟性が低い

作用の取り替え

  • モノイド作用のモノイドの取り替え
  • モイイド作用の状態空間の取り替え

状態空間Sの標準モノイド＝End(S)、作用の取り替え定理が成立する。

  • a:M×S→S が作用で、f:N→M がモノイド射（モノイドの圏の射＝モノイド準同型）のとき、新しい作用b:N×S→S が定義できる。
  • a:M×S→S が作用構造で、g:T→S, h:S→T が射（背景圏の射）で、ある条件を満たすならなら、新しい作用c:M×T→T が定義できる。

モナディックなクラアント／サーバー・アーキテクチャ

構成要素は：

  • クライアント側ライブラリ（便利関数群）
  • リクエスト・チャンネル
  • リクエスト・プロトコル
  • オペレーション・モノイド
  • アクション実装
  • 状態空間
クライアント側計算エージェント クライスリ射
リクエスト発行チャンネル クライスリ射のスタンピング出力成分
リクエスト・キューイング（累積） モノイド演算（乗法）
累積されたリクエスト モノイドの元
リクエスト実行（アクション） モノイド作用
状態空間 モノイドの被作用域（加群の台）


モノイダル・モナディックなクラアント／サーバーのメリット

  1. トランザクション内での遅延が可能。
  2. トランザクション単位での取り消し（巻き戻し；逆操作ではない）が可能。
  3. 状態空間を取り替えることができる。
  4. 状態空間に直接作用するモノイドを取り替えることができる。
  5. 状態空間と作用を準備してない状況でも実行できる。（自明状態空間）
  6. リクエストの集約、圧縮、最適化ができる。
  7. 複数の「状態空間＋作用」を直列につなぐことができる。
  8. リクエストの分岐ができる。並列処理ができる。
  9. サーバー側を変更しても、クライアントコードを一切変更する必要がない。
  10. よって、クライアントコードの再利用ができる。